Презентации по Математике

Алексе́й Андре́евич Ляпуно́в - советский математик, один из основоположников кибернетики, член-корреспондент АН СССР. Специалист в области теории функций вещественного переменного и математических вопросов кибернетики. Основные труды относятся к теории множеств, теоретическим вопросам программирования, математической лингвистике, математической биологии.

Синус, косинус, тангенс острого угла прямоугольного треугольника РАСПОЛОЖЕНИЕ УГЛОВ И СТОРОН А С В b c a АС – противолежащий катет ВС – прилежащий катет

Конъюнкция (логическое умножение). Соответствующие выражения языка: ·       Х и Y ·         Х вместе с Y ·         Х несмотря на Y ·         Х в то время, как Y ·         как Х так и Y                                        

∆EFD = ∆MKS Назовите пары соответственно равных элементов в равных треугольниках EF = MK FD = KS ED = MS Шесть пар соответственно равных элементов! Можно ли достроить треугольник, если известны три его

Модуль «ГЕОМЕТРИЯ» №11 Повторение (3) Ответ: 6. Найти площадь треугольника. В С А 8 3 30⁰ Повторение Площадь треугольника равна половине произведения двух сторон на синус угла между ними

Основные формулы дифференцирования Предполагается, что все рассматриваемые функции определены и дифференцируемы, причем все используемые значения принадлежат интервалу дифференцирования. 1. Производная постоянной величины равна 0. 2.Производная алгебраической суммы конечного числа дифференцируемых функций равна

What makes a business successful? Providing a service that customers like Building partnerships Being ahead of competitors Building brand value ...“Interactions” with customers, suppliers, competitors, regulators, people within the firm... What is game theory? ...a collection of

Основные обозначения и понятия: минор элемента aij : Mij ; алгебраическое дополнение элемента aij : Aij=(-1)i+j Mij ; матрица А-1 называется обратной матрицей к невырожденной квадратной матрице A (det A ≠ 0) , если выполняется условие A ∙

χ 2 – критерий Пирсона. Назначения критерия. Критерий χ2 применяется в двух целях: 1. Для сопоставления эмпирического распределения признака с теоретическим – равномерным, нормальным или каким-то иным; 2. Для сопоставления двух, трех и более эмпирических распределений одного и того

МПГУ ИФТИС Занятие заочникам 11.01.2017 Доцент кафедры ПМИиИТ Шапкина Вера Валерьевна for_ver@list.ru Пусть даны две переменные x и y с областями изменения X и Y. Предположим, что переменной x может быть приписано произвольное значение из области X без

Табличные случаи умножения и соответствующие им случаи деления, учащиеся должны усвоить на уровне навыка. Это сложный длительный процесс, в котором можно выделить два основных этапа. Первый этап связан с составлением таблиц. Второй этап связан с усвоением составленных таблиц, т.е их прочным

Неопределенность выбора элементов хi при создании сообщения удобно характе­ризовать энтропией источника H(x). При независимых элементах: При отсутствии взаимосвязи элементов: При зависимых элементах с условными вероятностями сначала определяется част­ная условная энтропия, вычисленная по предыдущей формуле, но в предположении зафиксированного предыдущего элемента

Окружность касается стороны АВ параллелограмма АВСD, пересекает стороны AD и ВС в точках М и N соответственно и проходит через вершины С и D. а) Докажите, что DN = CM. б) Найдите DN, зная, что АМ = 9, BN =

План лекции 1 Взаимное расположение двух прямых Прямые в пространстве могут быть: пересекающимися; скрещивающимися; параллельными (в частном случае совпадать) перпендикулярными (частный случай пересечения) 2

Жоспары: 1)Вариация көрсеткіштері туралы түсінік және оның міндеттері, түрлері 2)Вариациялық қатар ,вариациялық бөлу қатарлары 3) Бөлу қатарын графикалық түрде бейнелеу  Вариация көрсеткіштері туралы түсінік және оның міндеттері, түрлері Вариация – бұл зерттелетін жиынтықтың ішіндегі белгілердің жеке мәндерінің

Аксиомы метрического пространства Все эти расстояния удовлетворяют свойствам, принимаемым за аксиомы метрического пространства. А именно Метрическим пространством называется множество, для любых элементов A1, A2 которого определено неотрицательное число d(A1, A2), называемое расстоянием, для которого выполняются следующие свойства. 1. d(A1, A2) =

§4 Поверхности второго порядка Поверхности второго порядка описываются уравнениями второго порядка относительно переменных x, y, z. Среди поверхностей второго порядка выделим цилиндрические поверхности. Цилиндрическая поверхность Множество всех точек, лежащих на прямых (образующих), параллельных данной

Многие научные и инженерные задачи описываются с помощью таких математических моделей, для которых невозможно найти точного решения, т. е. выразить решение в аналитическом виде (в виде формул). В таких случаях для решения подбираются различные методы приближенных вычислений и разрабатываются

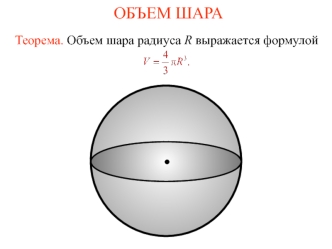
ОБЪЕМ ШАРОВОГО СЕГМЕНТА Шаровым сегментом называется часть шара, отсекаемая от него какой-нибудь плоскостью. Круг, образованный сечением шара этой плоскостью, называется основанием шарового сегмента. Часть диаметра шара, лежащая внутри шарового сегмента и перпендикулярная его основанию, называется высотой шарового сегмента. Теорема.

Цель Изучить историю возникновения лабиринтов Найти связь лабиринтов с нашей жизнью. Задачи Провести отбор материала, связанного с лабиринтами. Выявление различных методов нахождения выходов из лабиринтов и применение их к решению задач.

Формализация задачи оптимизации Формализация задачи оптимизации

I ТУР Ответ: ЦИФРА Вопрос № 1. Виктор Гюго заметил однажды, что разум человеческий владеет тремя

Цель урока: рассмотреть задачи на построение треугольника по трем элементам; совершенствовать навыки решения задач на построение. Чертёжные инструменты