- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Окружность. (Задача 18. Вариант 105) презентация
Содержание
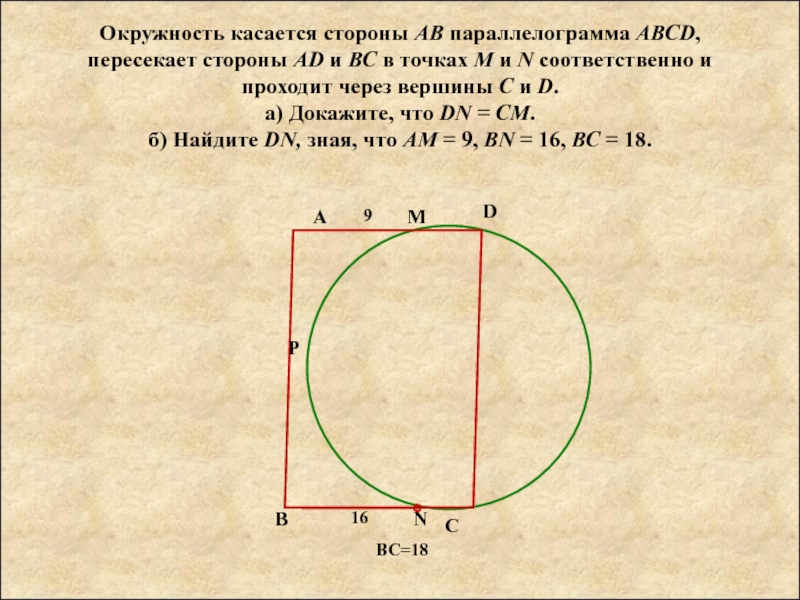
Слайд 2Окружность касается стороны АВ параллелограмма АВСD, пересекает стороны AD и ВС
Слайд 3Доказательство:
ABCD – параллелограмм, ⇒
MD || NC ⇒
Точки M, D, C, N – лежат на окружности, ⇒ трапеция NMDC вписана в окружность.
3. По свойству четырёхугольника, вписанного в окружность имеем,
∠ N + ∠ D = ∠ M + ∠ C = 180°.
∠ N и ∠ M – внутренние односторонние при MD || NC и MN – секущей ⇒ ∠ N + ∠ M = 180°.
Получаем, что ∠ D = ∠ M ⇒ трапеция NMDC равнобедренная ⇒ МС = ND.
Окружность касается стороны АВ параллелограмма АВСD, пересекает стороны AD и ВС в точках М и N соответственно и проходит через вершины С и D.
а) Докажите, что DN = CM.
б) Найдите DN, зная, что АМ = 9, BN = 16, ВС = 18.
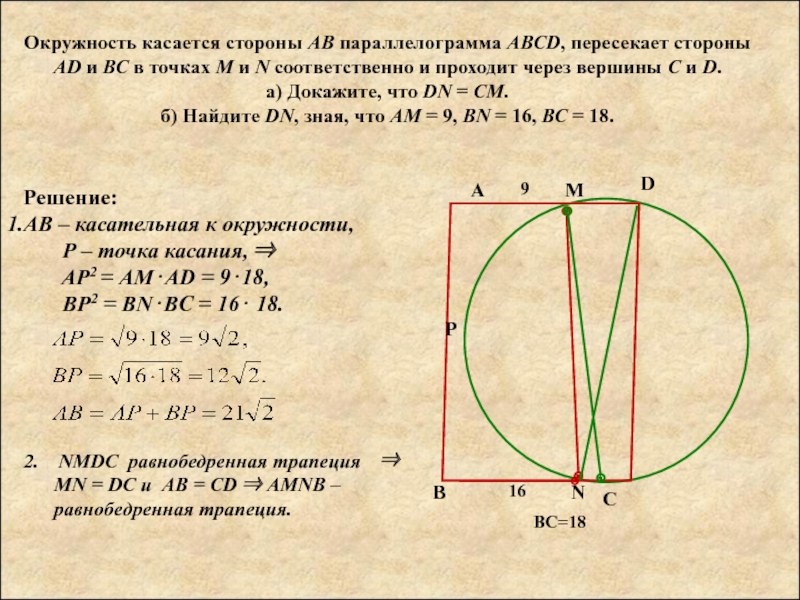
Слайд 4Окружность касается стороны АВ параллелограмма АВСD, пересекает стороны AD и ВС
Решение:
АВ – касательная к окружности,
Р – точка касания, ⇒
AР2 = АМ⋅AD = 9⋅18,
ВР2 = BN⋅BC = 16⋅ 18.
2. NMDC равнобедренная трапеция ⇒ MN = DC и AB = CD ⇒ AMNB – равнобедренная трапеция.
Слайд 5Окружность касается стороны АВ параллелограмма АВСD, пересекает стороны AD и ВС
А
N
В
M
9
16
Решение:
NMDC равнобедренная трапеция ⇒ MN = DC и AB = CD ⇒ AMNB – равнобедренная трапеция.
9
Н
К
3,5
3,5
С
2
2. ΔМКС – прямоугольный.
Ответ: ND = 30.