Презентации по Математике

Условные обозначения 2*2=4 Быть или не быть? Это самое важное, надо знать на 100%!!! Это надо решить и записать!!! Временные ряды

С О Х Р А Н И Т Ь З Р Е Н И Е н з и р е е С

Теория систем Система: пара множеств U, Y + отношение на множестве U×Y Свойства систем: Целостность; Структурированность; Целенаправленность дифференциальные и разностные уравнения, регрессионные модели, системы массового обслуживания, конечные и стохастические автоматы, дедуктивные системы (исчисления) Временные системы:

Сотую часть рубля называют копейкой, сотую часть доллара называют центом, сотую часть метра – сантиметром и т.д. Что такое ПРОЦЕНТ? Сотая часть квадрата Определение: сотая часть любой величины или числа называется ПРОЦЕНТОМ.

УСТОЙЧИВОСТЬ СЖАТЫХ СТЕРЖНЕЙ (ПРОДОЛЬНЫЙ ИЗГИБ) Форма равновесия в деформированном состоянии считается устойчивой, если система при любом малом отклонении от начального состояния равновесия возвращается к нему после снятия внешней нагрузки. В противном случае форма равновесия является неустойчивой.

Рассмотреть биографию Пифагора Познакомиться с его школой Собрать исторические сведения о теореме Исследовать различные способы доказательства Рассмотреть исторические и практические задачи на применении теоремы Пифагора Основные задачи Во времена Пифагора теорема звучала так:

ОСНОВНЫЕ ВОПРОСЫ: Сведения из истории графов. Граф и его элементы. Пути и маршруты в графах Связные графы. Деревья Операции над графами. Теория графов представляет собой раздел математики, имеющий широкие практические приложения. Теория графов – область дискретной

Девиз нашего урока : «Есть в математике нечто, вызывающее восторг» На уроках геометрии очень важно уметь смотреть и видеть, замечать и отмечать различные особенности геометрических фигур. «Установка» :

Понятие призмы Призмой называется многогранник, состоящий из двух плоских многоугольников (оснований призмы), которые лежат в разных плоскостях и совмещаются параллельным переносом, и всех отрезков, которые соединяют соответствующие точки этих многоугольников. Призма Отрезки, соединяющие соответствующие вершины, называются боковыми ребрами призмы. Многоугольники,

Это прямоугольный треугольник a c b катет Гипотенуза Катет

Основное определение  Графом G(V, Е) называется совокупность двух множеств — непустого множества V (множества вершин) и множества Е неупорядоченных пар различных элемен тов множества V (Е — множество ребер).   G ( V , E ) = { V, E},

Весёлый счёт Примерные задания: Показать все числа от 1 до 10. Какое число «соответствует» кукурузе (капусте и т.д.) (один у доски, остальные – веером могут показывать) 3. Назвать овощи чётных (нечётных) чисел. 4. Каким числам соответствуют овощи зелёного цвета? 5.

М О Д У Л Ь 0 −1,5 0,8 Для того, чтобы узнать тему нашего урока, укажите число, противоположное данному , а во второй таблице найдите букву, соответствующую этому числу. - это просто * * Модуль – это просто

Упражнение:          

Немного из истории Квадратные уравнения в Древнем Вавилоне Необходимость решать уравнения  не только первой, но и второй степени ещё в древности была вызвана потребностью решать задачи, связанные с нахождением площадей земельных участков и с земляными работами военного характера, а также с

Задачи на распознавание объекта В данных задачах требуется ответить на вопрос: принадлежит тот или иной объект объему данного понятия или не принадлежит. Например, установите, какие из фигур на рисунке 1 являются квадратами, а какие нет. Рис. 1

Цели урока: Ввести понятия: расстояние от точки до плоскости; расстояние между параллельными плоскостями; расстояние между скрещивающимися прямыми; Познакомиться с Теоремой о Трёх Перпендикулярах и с обратной теоремой; Задачи урока: Образовательные: получение и закрепление полученных знаний на

Найди «лишнее» Найди «лишнее»

Призмы Пирамиды

Проверка выполнения домашнего задания: №1100 ( в, г ) в) П о с т р о е н и е : 1) окр.( О; ОА1 ) 2) А1А3 = d A1 A3 3) A2A4 ┴

ПОНЯТИЕ ПРЯМОЙ И ОБРАТНОЙ ПРОПОРЦИОНАЛЬНОСТИ Пример 1 Пример 2 Миша шёл с постоянной скоростью 4 км/ч. Какое расстояние он пройдет за 1; 3; 6; 10 часов? Время и расстояние – это пропорциональные величины Чем больше часов будет идти

1.1. Экспериментирование как метод получения информации о системе Информация - это некоторая последовательность сведений, знаний, которые актуализируемы (получаемы, передаваемы, преобразуемы, сжимаемы и/или регистрируемы) с помощью некоторых знаков (символьного, образного, жестового, звукового, сенсомоторного типа) 1.1. Экспериментирование как метод получения информации о

Готовя варенье, на 2 кг слив кладут 3 кг сахара. Таким образом смешивают ингредиенты, т.е. составные части два к трем На пошив куртки от куска материи длиной 5 м отрезали 2 м, которые составляют 2/5 всего куска.

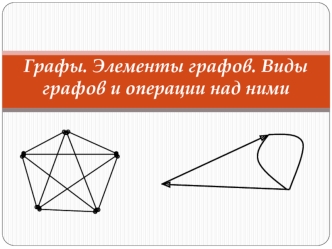
Базовые определения Рассматривают графы двух видов – ориентированные и неориентированные Ориентированный граф – это пара G(V,E), где V – произвольное непустое множество вершин, E – множество дуг, т.е. упорядоченных пар вершин (E⊆V×V). Неориентированный граф определяется аналогично, но E – множество неупорядоченных