Презентации по Математике

§4.1. Системы случайных величин Часто результат опыта описывается не одной случайной величиной X, а не- сколькими случайными величинами: Х1, Х2, …, Хn. В этом случае принято говорить, что указанные случайные величины образуют систему (Х1, Х2, …, Хn).

Исследование функций Теорема Ферма. Теорема Ролля. Теорема Лагранжа. Исследование функций Теорема Ферма. Пусть функция удовлетворяет условиям: Теорема Ролля. Теорема Лагранжа.

математика 7 5 1 способ 2 способ

Точна верхня межа     Точна верхня межа       Позначення.   супремум

CONTEÚDO PROGRAMÁTICO DESTA AULA Equações diferenciais de 1a ordem - continuação Método de Runge- Kutta (Euler modificado) EQUAÇÕES DIFERENCIAIS ORDINÁRIAS Uma Equação Diferencial Ordinária (EDO) é uma equação da forma F(x, y(x), y’(x),

Человечество всегда стремилось к некоторого рода предсказаниям. Любая наука основана на этом. Однако предвидение фактов не может быть абсолютным, каким бы обоснованным оно не казалось. У нас не может быть абсолютной уверенности в том, что наше предвидение не будет опровергнуто опытом.

А К М 48 30 78 78-48= 30 (МК)

Черепашков, А.А. Компьютерные технологии, моделирование и автоматизированные системы в машиностроении: учеб. для вузов по специальности "Автоматизация технологических процессов и производств (машиностроение)" Дёмин А.Ю. Основы компьютерной графики: учеб. пособие/А.Ю. Дёмин. – Томск: Из-во Томского политехнического университета, 2011. – 191 с. Роджерс, Д.,

№ 103 Отметьте в тетради точки A, B, C и D, так же как на рисунке 16. Постройте какую-нибудь другую незамкнутую ломаную, для которой эти точки тоже были бы вершинами. Запишите её название. A B C D

1 3 5 7 4 6 8 10 3 + 4 1 3 5 7 4 6 8 10 9 - 4

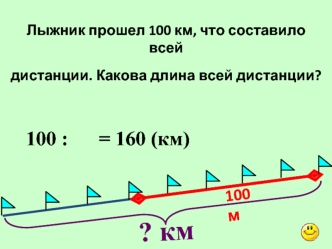
Задание 1) Решить заданное уравнение: y’-4xy=-4x^3,y(0)=-0.5 2) Показать и защитить презентацию на решение задачи Коши. 3) Продемонстрировать программу нахождения численного решения уравнения с помощью методов Эйлера и Рунге-Кутты 2-го порядка. 4) Нарисовать графики решений. 5) Проверить полученные результаты. 1

Вектор – направленный отрезок ya O Y X yb xb xa Координаты вектора с концами в точках A(xA, yA) и B(xB, yB) : Длина вектора a(x, y): Координаты суммы векторов a(xA, yA) и b(xB, yB)

§4. Непрерывность функции 1. Основные определения Пусть f(x) определена в некоторой окрестности точки x0 . ОПРЕДЕЛЕНИЕ 1. Функция f(x) называется непрерывной в точке x0 если справедливо равенство Замечания. 1) В силу теоремы 5 §3 равенство (1) можно записать в виде

Модель системы Пример классификации моделей системы (дихотомический подход) Система – объект, состоящий из некоторого множества частей, взаимодействующих друг с другом так, что знание поведения каждой из частей ещё не позволяет сделать выводы о

№ 236(а,б) S = 7 12 = 84 см2 b = 48 : 12 = 4 см а) 4 12 : 2 = 24 б) 25 4 – 1 8 2 = 64 в) 60 : 5 –

Задача 2. Построить сечение плоскостью, проходящей через точки Р, К, М, М∈ВС. К Р М Задача 3. Построить сечение плоскостью, проходящей через точки Т, Н, М, М∈АВ. Н Т М

Девиз урока: дорогу осилит идущий по ней человек. Друзья, сегодня вместе с героями мультфильма «По дороге с облаками» мы с вами продолжим решать уравнения. Успехов вам! Распределите предложенные примеры по столбикам (274+323):3;

Цель лекции: изучить основные понятия дифференциального исчисления, геометрический смысл производной, правила вычисления производной и дифференциала, производные сложной функции, производные высших порядков Материально-техническое обеспечение: компьютер, видеопроектор, экран Учебно-методическое обеспечение: учебно-методический материал в электронном виде, программный комплекс «Дифференциальное исчисление» Основные вопросы

Цель: повторение основных понятий, законов и формул ОСНОВ СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ в соответствии с кодификатором ЕГЭ. Элементы содержания, проверяемые на ЕГЭ 2010: Постулаты теории относительности Эйнштейна Полная энергия Энергия покоя. Дефект массы и энергия связи

  Как и многие разделы математики, тригонометрия возникла в древние времена из потребностей людей при ведении расчётов, связанных с земельными работами (для определения расстояния до недоступных предметов, составления географических карт и прочее). Древнегреческие математики,

Для изучения темы: «Масштаб» нам потребуется ответить на ряд вопросов 1. Что такое отношение? 2. Что такое пропорция? 3. Сформулируйте основное свойство пропорции. 4. Где вы уже встречались с «Масштабом»? 5. Сколько сантиметров в одном метре; сколько сантиметров в одном километре;

РАЗМИНКА Выполните действия 7/9 + 1/9 3/5 + 4/5 – 2/5     Представьте в виде суммы произведение: n*

Математическую модель САУ используют для изучения работы систем автоматического регулирования при установившемся режиме работы, а также в переходных режимах. Тема 6. «Математические модели САУ» Дифференциальное уравнение САУ ai, bi - постоянные коэффициенты, у – управляемая (выходная) величина, х –