в памяти.
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Алгоритмы на графах презентация
Содержание
- 1. Алгоритмы на графах
- 2. Базовые определения Рассматривают графы двух видов –
- 3. Базовые определения Особые случаи дуг/рёбер: петля, кратные
- 4. Базовые определения Две дуги (ребра) называются кратными,
- 5. Базовые определения Рассмотрим дугу (ребро) e=(u,v). Говорят,
- 6. Базовые определения Степень вершины – это количество
- 7. Теорема Теорема 1. Для любого неориентированного графа
- 8. Базовые определения Путём на ориентированном графе называется
- 9. Базовые определения Путь (цепь) называется простым, если
- 10. Теорема Теорема 3. Если в графе степень
- 11. Способы представления графов Матрица смежности: для неориентированного
- 12. Способы представления графов Матрица инцидентности: для неориентированного
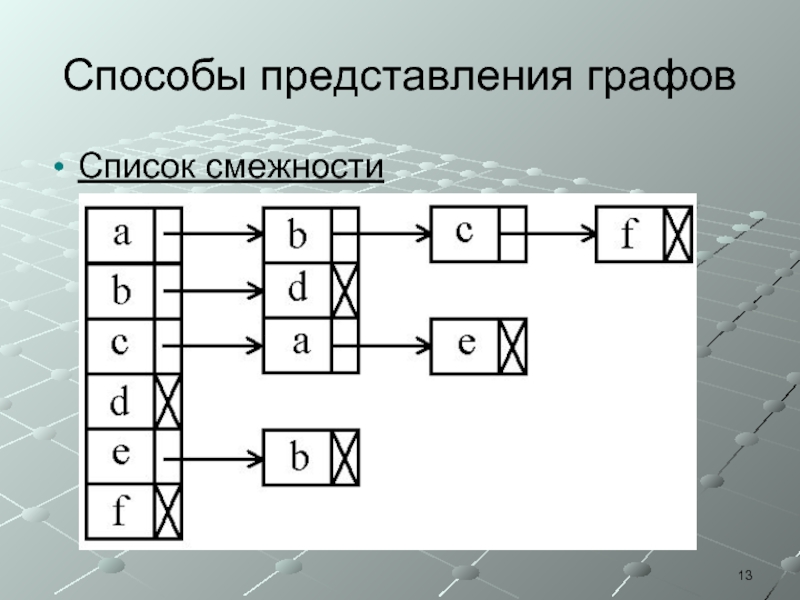
- 13. Способы представления графов Список смежности
- 14. Способы представления графов Модифицированный список смежности Два
- 15. Рекомендуемая литература Ерусалимский Я.М. Дискретная математика: теория,
Слайд 1Алгоритмы на графах
Базовые определения.
Несколько простых, но важных теорем.
Способы представления
Слайд 2Базовые определения
Рассматривают графы двух видов – ориентированные и неориентированные
Ориентированный граф –
это пара G(V,E), где V – произвольное непустое множество вершин, E – множество дуг, т.е. упорядоченных пар вершин (E⊆V×V).
Неориентированный граф определяется аналогично, но E – множество неупорядоченных пар вершин. Элементы E называются рёбрами.
Неориентированный граф определяется аналогично, но E – множество неупорядоченных пар вершин. Элементы E называются рёбрами.
Слайд 3Базовые определения
Особые случаи дуг/рёбер: петля, кратные дуги/рёбра.
Петлёй называется дуга (для неориентированного
графа - ребро), соединяющая вершину с ней же. Например:
Слайд 4Базовые определения
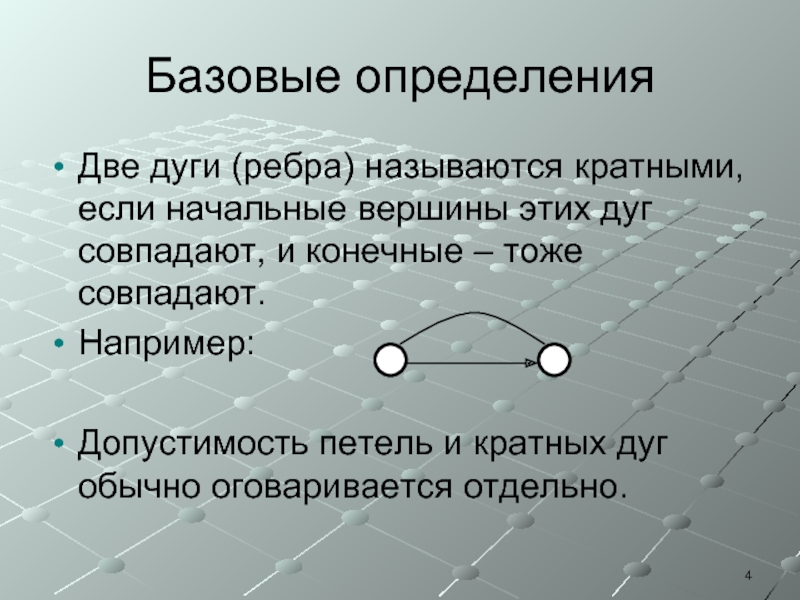
Две дуги (ребра) называются кратными, если начальные вершины этих дуг
совпадают, и конечные – тоже совпадают.
Например:
Допустимость петель и кратных дуг обычно оговаривается отдельно.
Например:
Допустимость петель и кратных дуг обычно оговаривается отдельно.
Слайд 5Базовые определения
Рассмотрим дугу (ребро) e=(u,v).
Говорят, что дуга e инцидентна вершинам u
и v.
Аналогично, вершина u и вершина v инцидентны дуге e.
Вершины u и v называются смежными.
Дуги (рёбра), имеющие общую вершину, также называются смежными.
Аналогично, вершина u и вершина v инцидентны дуге e.
Вершины u и v называются смежными.
Дуги (рёбра), имеющие общую вершину, также называются смежными.
Слайд 6Базовые определения
Степень вершины – это количество дуг (рёбер), которым инцидентна данная
вершина.
Степень вершины v обозначается deg(v).
Для ориентированных графов выделяют также полустепень исхода deg-(v) и полустепень захода deg+(v).
Степень вершины v обозначается deg(v).
Для ориентированных графов выделяют также полустепень исхода deg-(v) и полустепень захода deg+(v).
Слайд 7Теорема
Теорема 1. Для любого неориентированного графа сумма deg(v) по всем v∈V
равна 2|V|.
Следствие. На любом графе количество вершин нечетной степени четно.
Аналог теоремы 1 для орграфов:
Теорема 2. Для любого орграфа сумма степеней захода равна сумме степеней исхода. И эти суммы равны количеству вершин графа.
Следствие. На любом графе количество вершин нечетной степени четно.
Аналог теоремы 1 для орграфов:
Теорема 2. Для любого орграфа сумма степеней захода равна сумме степеней исхода. И эти суммы равны количеству вершин графа.
Слайд 8Базовые определения
Путём на ориентированном графе называется последовательность вершин v1, v2, …,
vk, в которой для любого i вершины vi и vi+1 соединены дугой.
Путь можно понимать и как последовательность дуг.
Для неориентированного графа аналогичная последовательность вершин/рёбер называется цепью.
Путь можно понимать и как последовательность дуг.
Для неориентированного графа аналогичная последовательность вершин/рёбер называется цепью.
Слайд 9Базовые определения
Путь (цепь) называется простым, если в нём все вершины (за
исключением, может быть, крайних) различны.
Контуром (циклом) называется путь (цень), у которого начальная и конечная вершина совпадают.
Контуром (циклом) называется путь (цень), у которого начальная и конечная вершина совпадают.
Слайд 10Теорема
Теорема 3. Если в графе степень любой вершины больше или равна
2, то в этом графе существует цикл.
Аналогичная теорема для ориентированных графов:
Теорема 4. Если в ориентированном графе для любой вершины v deg-(v)≥0 и deg+(v) ≥0, то на данном орграфе существует контур.
Аналогичная теорема для ориентированных графов:
Теорема 4. Если в ориентированном графе для любой вершины v deg-(v)≥0 и deg+(v) ≥0, то на данном орграфе существует контур.
Слайд 11Способы представления графов
Матрица смежности:
для неориентированного графа
для ориентированного графа –
аналогично.
Слайд 12Способы представления графов
Матрица инцидентности:
для неориентированного графа
для ориентированного графа:
Слайд 14Способы представления графов
Модифицированный список смежности
Два массива: A и P.
В массиве A
подряд записаны списки смежных вершин для всех вершин графа, в порядке нумерации. То есть массив A имеет размер |E|.
В массиве P элемент p[i] равен индексу в массиве A, начиная с которого расположен список смежных вершин для vi.
В массиве P элемент p[i] равен индексу в массиве A, начиная с которого расположен список смежных вершин для vi.
Слайд 15Рекомендуемая литература
Ерусалимский Я.М. Дискретная математика: теория, задачи, приложения. – М.: Вузовская
книга, 2006 г. : 268 с.
Кристофидес Н. Алгоритмы на графах. — М.: Мир, 1974.
Носов В.А. «Комбинаторика и теория графов», курс лекций. http://intsys.msu.ru/staff/vnosov/combgraph.htm
Кристофидес Н. Алгоритмы на графах. — М.: Мир, 1974.
Носов В.А. «Комбинаторика и теория графов», курс лекций. http://intsys.msu.ru/staff/vnosov/combgraph.htm