Презентации по Математике

СИМПЛЕКСНЫЙ МЕТОД ПЛАНИРОВАНИЯ Метод симплексного планирования позволяет без предварительного изучения влияния факторов найти область оптимума. В этом методе не требуется вычисления градиента функции отклика, поэтому он относится к безградиентным методам поиска оптимума. Для этого используется специальный план эксперимента в виде симплекса.

Множество – группа предметов с общим названием и собранных вместе Множества могут иметь: Много элементов; Ни одного элемента; 1 или 2 элемента; Примеры Множеств, в которых

1. Переместительный A v B = B v A A & B = B & A 2. Сочетательный (A v B) v C = A v (B v C) (A & B) & C

Огюстен Луи Коши - французский математик XIX века, который вошел в историю благодаря открытиям в области дифференциальных уравнений, алгебры, геометрии и математического анализа. Многие открытия ученого названы в его честь и применяются поныне. Детство и юность Огюстен Луи

Содержание: Рандомизированное полноблочное планирование Статистический анализ Оценивание недостающих данных Рандомизированное полноблочное планирование

2. Применение множественного корреляционно-регрессионного анализа Экономические явления часто определяются большим числом одновременно и совокупно действующих факторов. Задача состоит в исследовании зависимости переменной у от объясняющих переменных х1, х2, х3…. 3. Задачи множественного корреляционно-регрессионного анализа

Параллельные прямые в пространстве 1 Каково может быть взаимное расположение двух прямых на плоскости? © Кузьмина Е.А., Колобовская МСОШ, 2010 2 Дайте определение параллельных прямых на плоскости. Параллельные прямые в пространстве © Кузьмина Е.А., Колобовская МСОШ, 2010 Параллельными

§ 5. Кривые второго порядка   § 5. Кривые второго порядка Такие линии называются кривыми второго порядка. Установим при каких условиях уравнение определяет окружность, эллипс, гиперболу или параболу.

ІІ. Мета уроку: Систематизувати знання учнів по темі : “Паралелограм ”. Спонукати учнів до творчої діяльності. Формувати математичну компетентність, навики розв’язування задач з використанням властивостей та ознак паралелограма, самостійності у роботі, вміння працювати в команді, комунікабельність, підвищення рівня

Понятие предиката Выразительные возможности языка логики высказываний очень ограничены. С ее помощью невозможно проанализировать внутреннюю структуру даже очень простых рассуждений. Пример: есть два умозаключения. Любой человек смертен, Сократ - человек, следовательно, Сократ смертен. Крокодилы не летают, Луна

В А С Равнобедренный треугольник О С Н О В А Н И Е БОКОВАЯ СТОРОНА БОКОВАЯ СТОРОНА Равносторонний треугольник N M O В А С Тренировочные задания. Р = 15,6

МЕДИЦИНА И МАТЕМАТИКА

Умение по формуле понять какое изменение происходит, с аргументом или с функцией. изменение на несколько единиц в несколько раз на противоположное аргумента функции y=sinx y=sinx y=sinx y=cosx y=cosx y=sinx-1,5 y=cos(x+π/3) y=2cosx y=sin2x y=-sinx

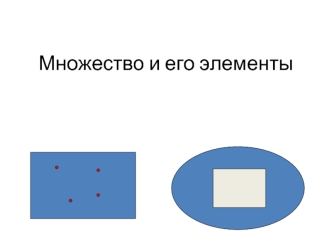
Понятие множества Множество – это неопределяемое понятие. Множество это объединение, совокупность, собрание объектов, объединённых общими свойствами. Примеры: Множество дней недели Множество студентов в группе 1Н Понятие элементов множества Элементы множества – объекты, составляющие данное множество. Примеры: Множество

Прямая на плоскости Уравнение прямой, проходящей через точку перпендикулярно вектору

Модели и моделирование Требования, предъявляемые к моделям

Рене Декарт – французский философ, математик, физик и физиолог. (1596-1650). Автор координатной плоскости, поэтому ее часто называют декартовой системой координат. ось абсцисс ось ординат Y ПРЯМОУГОЛЬНАЯ (ДЕКАРТОВА) СИСТЕМА КООРДИНАТ О X начало координат

11. ТЕОРИЯ ДВОЙСТВЕННОСТИ В ЛИНЕЙНОМ ПРОГРАММИРОВАНИИ (ПРОДОЛЖЕНИЕ) 11.5. Теоремы двойственности и равновесия. 11.5. Теоремы двойственности и равновесия. Справедлива следующая теорема, которую обычно называют теоремой двойственности.

Решение задач условно можно разделить на несколько шагов

Основной вопрос: Как связано понятие вероятности с геометрией? Задачи: Провести серию опытов. Сформулировать геометрическое понятие вероятности. Изучить литературу по данному вопросу. Сделать выводы. Подтвердить или опровергнуть гипотезу. Составить задачи на нахождение вероятностей. Серия опытов.

Содержание Первый признак равенства треугольников Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны. A B C B1 A1 C1 AB=A1B1 BC=B1C1

Если функция f(x)>0 на [a,b], то значение функции Ф(x) в точке x равно площади под кривой y=f(x) на отрезке [a,х]. S СВОЙСТВА ИНТЕГРАЛА С ПЕРЕМЕННЫМ ВЕРХНИМ ПРЕДЕЛОМ Теорема 1. Если функция f(x) непрерывна на отрезке

Устно: 19см= мм, 3м45см= см, 8км= м, 1км205м= м, 2км80м= м, 15004м= км м, 6о см= дм,