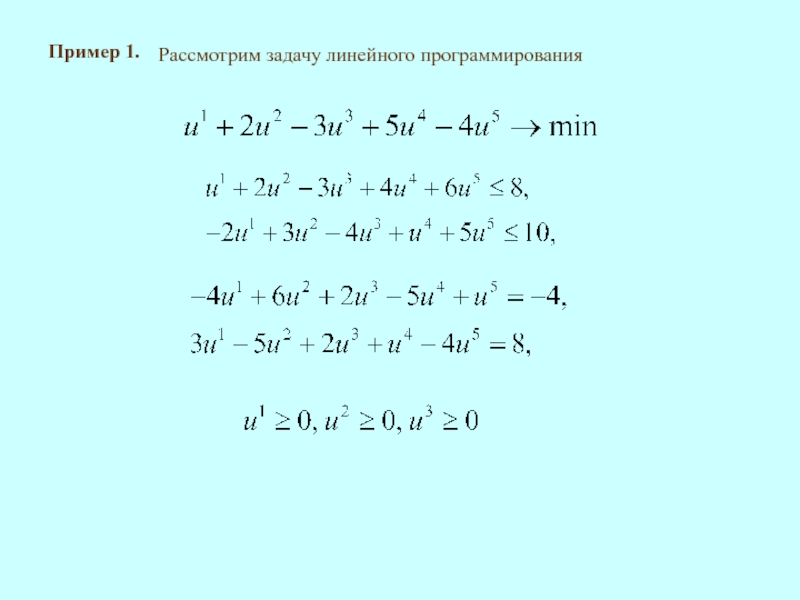- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Выпуклый анализ. Теория двойственности в линейном программировании. Лекция 29 презентация
Содержание
Слайд 2
11. ТЕОРИЯ ДВОЙСТВЕННОСТИ В ЛИНЕЙНОМ
ПРОГРАММИРОВАНИИ (ПРОДОЛЖЕНИЕ)
11.5. Теоремы двойственности и равновесия.
Слайд 3
11.5. Теоремы двойственности и равновесия.
Справедлива следующая теорема,
которую обычно называют
Теорема 1.
либо они обе имеют решение и
не имеют решения,
Доказательство.
Выпишем функцию Лагранжа для задачи 3.
Слайд 6
Пусть
Тогда
Таким образом,
Пусть одна из взаимно двойственных задач имеет решение.
Тогда по теореме
функции Лагранжа для этой задачи.
При этом
Слайд 7
Выше установлено, что
Тогда по теореме 9.2
В силу (1)
справедливо равенство
Аналогично устанавливается, что
следует
Теорема доказана.
Установим условия разрешимости взаимно двойственных задач.
Для существования решения взаимодвойственных задач достаточно,
чтобы обе взаимодвойственные задачи были допустимыми.
Теорема 2.
из существования решения двойственной задачи
что если одна из взаимно двойственных задач не имеет решения,
Доказательство.
Тогда
Слайд 14
Построим двойственную к ней задачу:
является допустимой для прямой задачи,
так
Слайд 16
По теореме 2 обе взаимодвойственные задачи имеют решение.
Решение прямой задачи:
Решение двойственной задачи:
В соответствии с теоремой 1 здесь выполнено равенство
Действительно,
,
Выпишем эти решения.
В силу теоремы 3