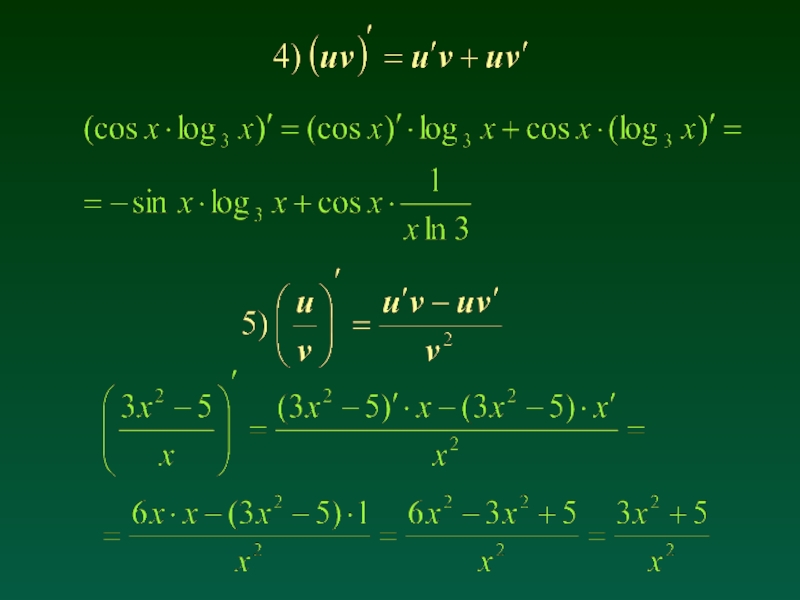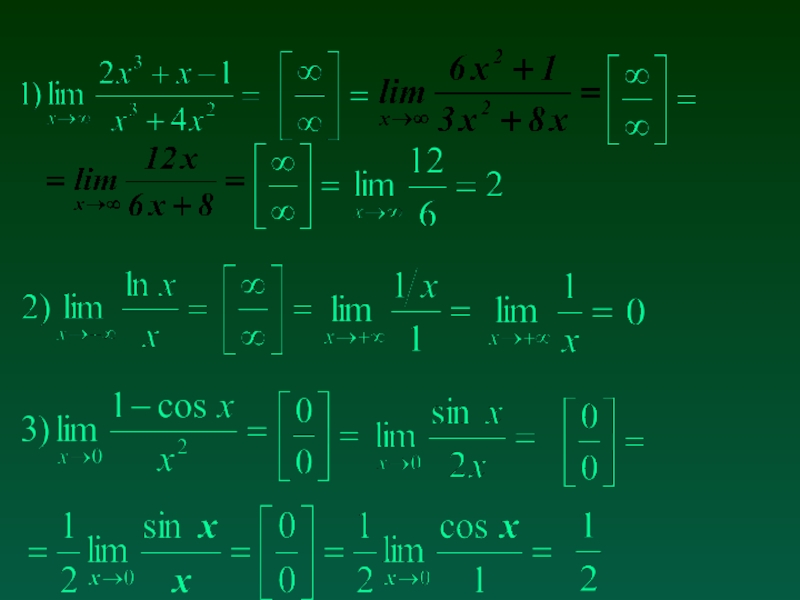Подготовил
к.п.н., доцент
Третьякова Н.В.
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Дифференциальное исчисление презентация
Содержание
- 1. Дифференциальное исчисление
- 2. Цель лекции: изучить основные понятия дифференциального исчисления,
- 3. Основные вопросы 1. Понятие производной 2.
- 4. Рекомендуемая литература Быкова О., Колягин С.,
- 5. Рекомендуемая литература Математика: Учебное пособие /
- 6. Электронные ресурсы: - www.iprbookshop.ru, http://www.iprbookshop.ru -
- 7. 1. Понятие производной Производной функции y =
- 8. Найти производную функции по определению
- 9. Касательной к графику функции y = f(x)
- 10. 3. Формулы дифференцирования элементарных функций
- 11. 4. Основные правила дифференцирования Пусть u =
- 13. 5. Дифференциал функции Дифференциалом функции y
- 14. 6. Производная сложной функции Если y
- 15. 7. Производные высших порядков
- 16. 8. Правило ЛОПИТАЛЯ Пусть тогда или и
- 18. БЛАГОДАРЮ за внимание!
Цель лекции: изучить основные понятия дифференциального исчисления, геометрический смысл производной, правила вычисления производной и дифференциала, производные сложной функции, производные высших порядков Материально-техническое обеспечение: компьютер, видеопроектор, экран Учебно-методическое обеспечение: учебно-методический материал в
Слайд 1Лекция
Тема
ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
по дисциплине «Математика»
Краснодар
2015
Российский университет кооперации
Краснодарский кооперативный институт
Кафедра информационных
технологий и математики
Слайд 2Цель лекции: изучить основные понятия дифференциального исчисления, геометрический смысл производной, правила
вычисления производной и дифференциала, производные сложной функции, производные высших порядков
Материально-техническое обеспечение: компьютер, видеопроектор, экран
Учебно-методическое обеспечение: учебно-методический материал в электронном виде, программный комплекс «Дифференциальное исчисление»
Материально-техническое обеспечение: компьютер, видеопроектор, экран
Учебно-методическое обеспечение: учебно-методический материал в электронном виде, программный комплекс «Дифференциальное исчисление»
Слайд 3Основные вопросы
1. Понятие производной
2. Геометрический смысл производной
3. Формулы дифференцирования элементарных функций
4. Основные
правила дифференцирования
5. Дифференциал функции
6. Производная сложной функций
7. Производные высших порядков
8. Правило Лопиталя
9. Формула Тейлора
5. Дифференциал функции
6. Производная сложной функций
7. Производные высших порядков
8. Правило Лопиталя
9. Формула Тейлора
Слайд 4Рекомендуемая литература
Быкова О., Колягин С., Кукушкин Б. Практикум по математическому анализу.
- М., 2011, 276 с.
Геворкян Э. А. Математика. Математический анализ. Учебно-методический комплекс.-М.: Евразийский открытый институт, 2010.- 343 с. http://biblioclub.ru/index.php?page=book&id=93168
Гусак А.А. Высшая математика. Часть 1. М.: Высшая школа, 2005.
Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. Т1, Т2. М., Высшая школа, 1997.
Демидович В.П. Сборник задач и упражнений по математическому анализу. М., Наука, 1990.
Курзина, В.М. Математика.[текст]: Практическое пособие/В.М. Курзина, В.В. Казей, Д. С. Васильева.-М.:РУК,2010.-105 с
Математика: Учебник / А.А. Дадаян. - 3-e изд. - М.: Форум, 2010. - 544 с.: 60x90 1/16. - (Профессиональное образование). http://znanium.com/bookread.php?book=242366
Геворкян Э. А. Математика. Математический анализ. Учебно-методический комплекс.-М.: Евразийский открытый институт, 2010.- 343 с. http://biblioclub.ru/index.php?page=book&id=93168
Гусак А.А. Высшая математика. Часть 1. М.: Высшая школа, 2005.
Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. Т1, Т2. М., Высшая школа, 1997.
Демидович В.П. Сборник задач и упражнений по математическому анализу. М., Наука, 1990.
Курзина, В.М. Математика.[текст]: Практическое пособие/В.М. Курзина, В.В. Казей, Д. С. Васильева.-М.:РУК,2010.-105 с
Математика: Учебник / А.А. Дадаян. - 3-e изд. - М.: Форум, 2010. - 544 с.: 60x90 1/16. - (Профессиональное образование). http://znanium.com/bookread.php?book=242366
Слайд 5Рекомендуемая литература
Математика: Учебное пособие / Н.А. Березина, Е.Л. Максина. - М.:
ИЦ РИОР: НИЦ Инфра-М, 2013. - 175 с. http://znanium.com/bookread.php?book=369492
Математика: Учебник / А.А. Дадаян. - 3-e изд. - М.: Форум: НИЦ ИНФРА-М, 2013. - 544 с. http://znanium.com/bookread.php?book=397662
Математика: Учебное пособие / Ю.М. Данилов, Н.В. Никонова, С.Н. Нуриева; Под ред. Л.Н. Журбенко, Г.А. Никоновой. - М.: НИЦ ИНФРА-М, 2014. - 496 с. http://znanium.com/bookread.php?book=471655
Пухначев Ю. Семь семинаров по математическому анализу. – М.: 2012, 592 с.
Туганбаев А. А. Дифференциальные уравнения: Учебное пособие.-3-е издание.-М.: Издательство «ФЛИНТА», 2012.-34 с. http://biblioclub.ru/index.php?page=book&id=115139
Шапкин А. С. Математические методы и модели исследования операций: Учебник.-М.: Дашков и Ко, 2012.-397 с. http://biblioclub.ru/index.php?page=book&id=112204
Шипачев В.С. Высшая математика. М.: Высшая школа, 2006.
Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления. Т. 1, Т .2
Математика: Учебник / А.А. Дадаян. - 3-e изд. - М.: Форум: НИЦ ИНФРА-М, 2013. - 544 с. http://znanium.com/bookread.php?book=397662
Математика: Учебное пособие / Ю.М. Данилов, Н.В. Никонова, С.Н. Нуриева; Под ред. Л.Н. Журбенко, Г.А. Никоновой. - М.: НИЦ ИНФРА-М, 2014. - 496 с. http://znanium.com/bookread.php?book=471655
Пухначев Ю. Семь семинаров по математическому анализу. – М.: 2012, 592 с.
Туганбаев А. А. Дифференциальные уравнения: Учебное пособие.-3-е издание.-М.: Издательство «ФЛИНТА», 2012.-34 с. http://biblioclub.ru/index.php?page=book&id=115139
Шапкин А. С. Математические методы и модели исследования операций: Учебник.-М.: Дашков и Ко, 2012.-397 с. http://biblioclub.ru/index.php?page=book&id=112204
Шипачев В.С. Высшая математика. М.: Высшая школа, 2006.
Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления. Т. 1, Т .2
Слайд 6
Электронные ресурсы:
- www.iprbookshop.ru, http://www.iprbookshop.ru
- Научная электронная библиотека eLIBRARY.RU http://elibrary.ru
-
Электронная библиотека Grebennikon httphttp.//http.//grebennikonhttp.//grebennikon.http.//grebennikon.ru/
- Универсальная справочно-информационная полнотекстовая база данных периодических изданий East View httphttp://http://ebibliotekahttp://ebiblioteka.http://ebiblioteka.ruhttp://ebiblioteka.ru/
- Электронная библиотечная система znanium.com
- Универсальная справочно-информационная полнотекстовая база данных периодических изданий East View httphttp://http://ebibliotekahttp://ebiblioteka.http://ebiblioteka.ruhttp://ebiblioteka.ru/
- Электронная библиотечная система znanium.com
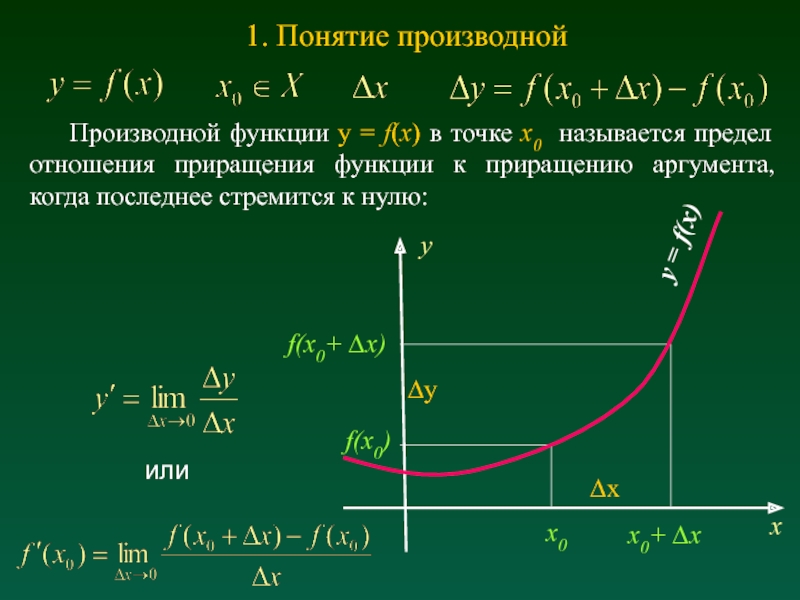
Слайд 71. Понятие производной
Производной функции y = f(x) в точке x0 называется
предел отношения приращения функции к приращению аргумента, когда последнее стремится к нулю:
или
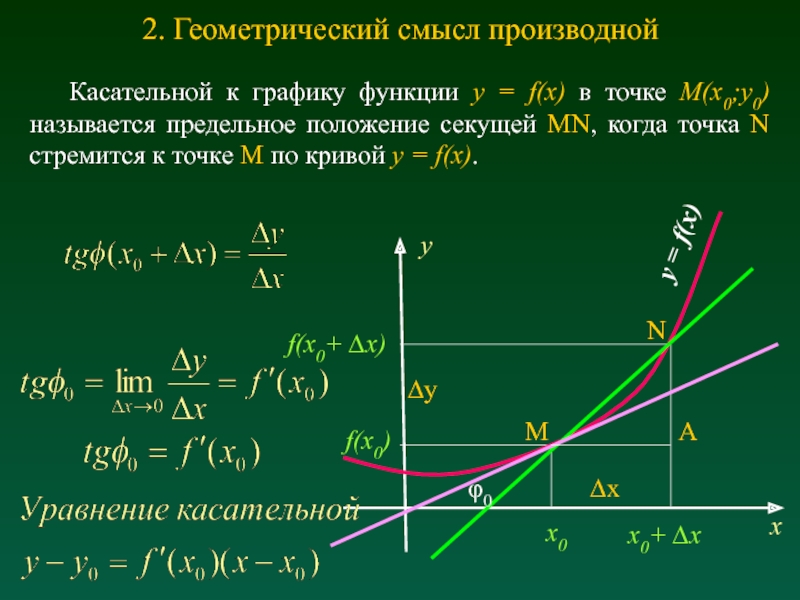
Слайд 9 Касательной к графику функции y = f(x) в точке M(x0;y0) называется
предельное положение секущей MN, когда точка N стремится к точке M по кривой y = f(x).
2. Геометрический смысл производной
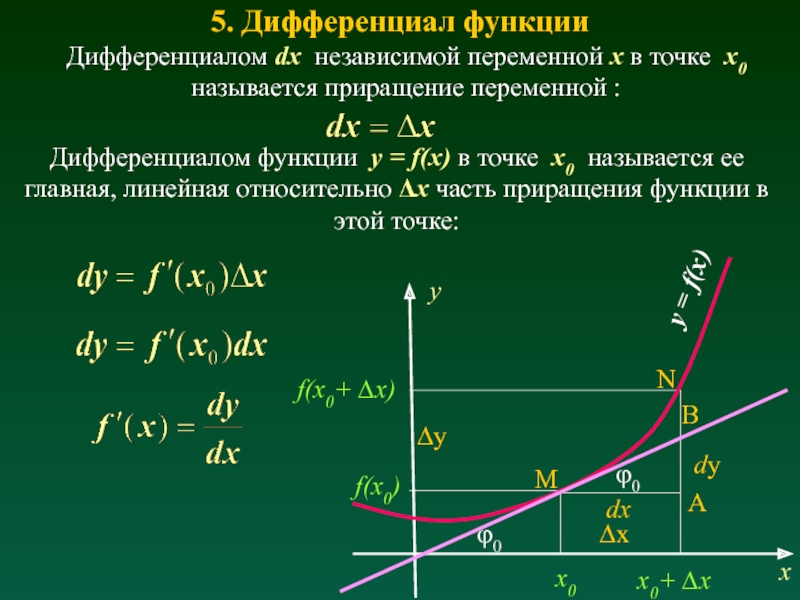
Слайд 135. Дифференциал функции
Дифференциалом функции y = f(x) в точке x0 называется
ее главная, линейная относительно Δx часть приращения функции в этой точке:
Дифференциалом dx независимой переменной x в точке x0 называется приращение переменной :
Слайд 146. Производная сложной функции
Если y = f(u) , а u =
φ(x), т.е. y = f(φ(x)),
a функции f(u) и φ(x) имеют производные, тогда
a функции f(u) и φ(x) имеют производные, тогда
Слайд 157. Производные высших порядков
Производной n порядка называется производная
от производной n - 1 порядка:
