- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Исследование функций и построение графиков. Теоремы Ферма, Ролля, Лагранжа презентация
Содержание
- 1. Исследование функций и построение графиков. Теоремы Ферма, Ролля, Лагранжа
- 2. Исследование функций Теорема Ферма. Теорема Ролля. Теорема Лагранжа.
- 3. Исследование функций Теорема Ферма.
- 4. Исследование функций Теорема
- 5. Исследование функций Теорема
- 6. Исследование
- 7. Исследование
- 14. Исследование функций Монотонность функции. Определение 1. Функция
- 15. Исследование функций Теорема. Пусть Тогда: Доказательство. 1. 2. 3.
- 16. Исследование функций Экстремум функции. Определение 1. Точка
- 17. Исследование функций Необходимый признак экстремума. Теорема. 1.
- 18. Исследование функций Достаточные признаки экстремума. Определение. Пусть
- 19. Исследование функций Первый достаточный признак экстремума. Теорема.
- 20. Исследование функций Второй достаточный признак экстремума. Теорема.
- 21. Исследование функций Выпуклость и точки перегиба графика
- 22. Исследование функций Достаточный признак выпуклости. Теорема. 1.
- 23. Исследование функций Необходимый признак перегиба. Теорема. 1.
- 24. Исследование функций Асимптоты графика функции. Определение. Прямая
- 25. Исследование функций Асимптоты графика функции. Определение. Прямая
- 26. Исследование функций Асимптоты графика функции. Определение. Прямая
- 27. Исследование функций Теорема 1. Прямая
- 28. Исследование функций Общая схема исследования функции. Первый
- 29. Исследование функций Пример 1. Исследовать функцию и
- 30. Исследование функций 5. Асимптоты. а) вертикальных асимптот
- 31. Исследование функций Исследование с помощью первой производной.
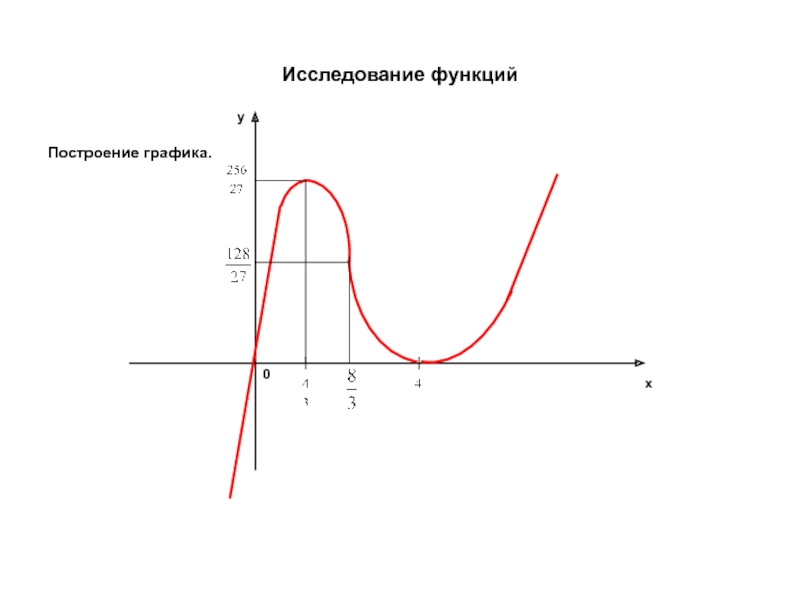
- 32. Исследование функций Построение графика. x y 0
- 33. Исследование функций Исследование с помощью второй производной. х + -
- 34. Исследование функций Построение графика. x y 0
- 35. Исследование функций Пример 2. Исследовать функцию и
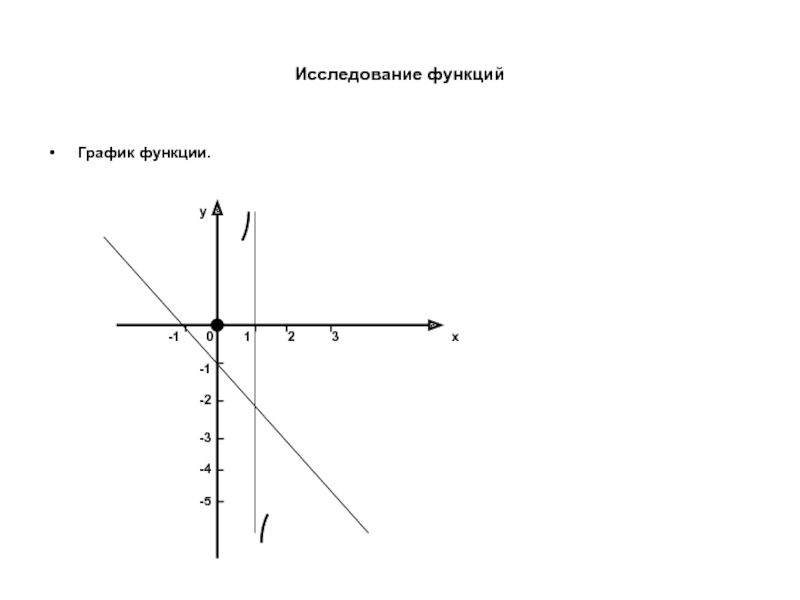
- 36. Исследование функций График функции. 0 x y
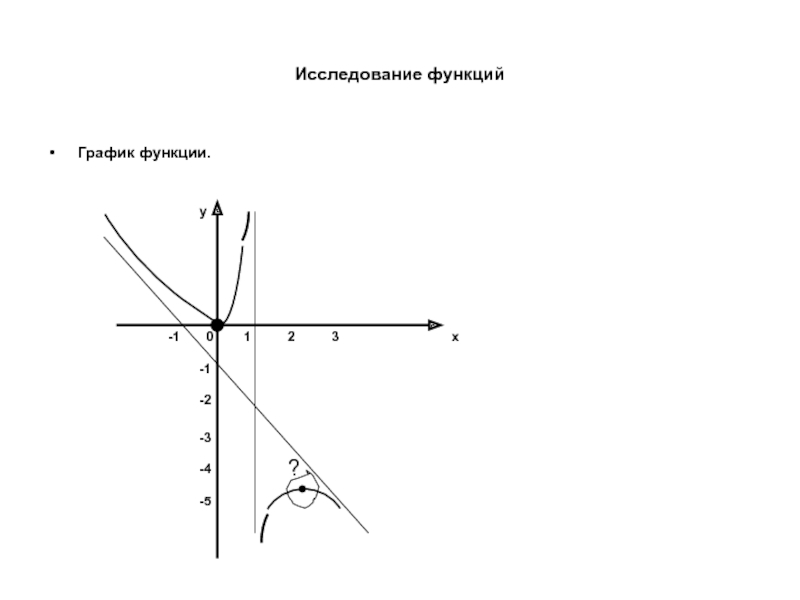
- 37. Исследование функций График функции.
- 38. Исследование функций Исследование с помощью первой производной. x 0 1 2
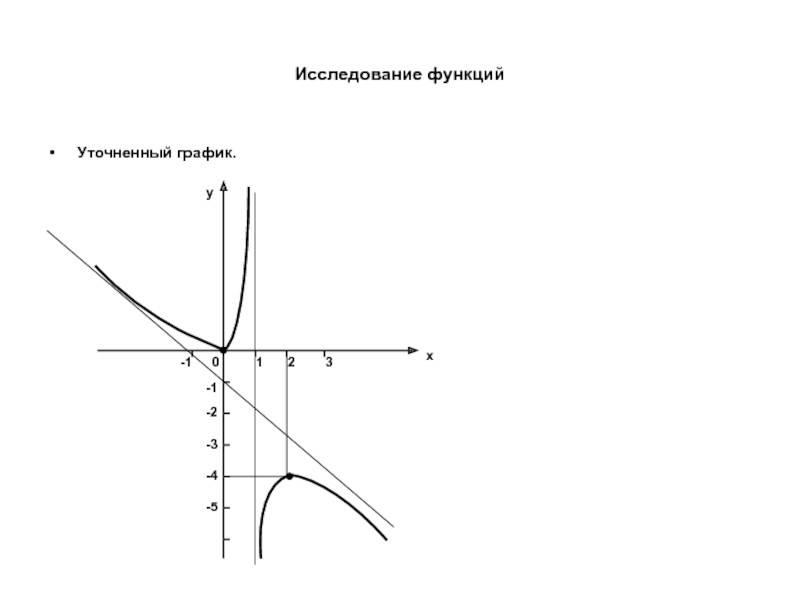
- 39. Исследование функций Уточненный график. x y 0
Слайд 3
Исследование функций
Теорема Ферма.
Пусть функция
удовлетворяет условиям:
Теорема Ролля.
Теорема Лагранжа.
Слайд 4
Исследование функций
Теорема Ферма.
Пусть функция
удовлетворяет условиям:
а) непрерывна на отрезке [a,b];
б) имеет производную
во всех внутренних точках (a,b);
в) принимает наибольшее или
наименьшее значение
во внутренней точке c є (a,b).
Тогда :
Теорема Ролля.
Теорема Лагранжа.
Слайд 5
Исследование функций
Теорема Ферма.
Пусть функция
удовлетворяет условиям:
а) непрерывна на отрезке [a,b];
б) имеет производную
во всех внутренних точках (a,b);
в) принимает наибольшее или
наименьшее значение
во внутренней точке c є (a,b).
Тогда :
Теорема Ролля.
Пусть функция
удовлетворяет условиям:
Теорема Лагранжа.
Пусть функция
удовлетворяет условиям:
Слайд 6
Исследование функций
Теорема Ферма.
Пусть функция
удовлетворяет условиям:
а) непрерывна на отрезке [a,b];
б) имеет производную
во всех внутренних точках (a,b);
в) принимает наибольшее или
наименьшее значение
во внутренней точке c є (a,b).
Тогда :
Теорема Ролля.
Пусть функция
удовлетворяет условиям:
Теорема Лагранжа.
Пусть функция
удовлетворяет условиям:
а) непрерывна на отрезке [a,b];
б) имеет производную
во всех внутренних точках (a,b);
Слайд 7
Исследование функций
Теорема Ферма.
Пусть функция
удовлетворяет условиям:
а) непрерывна на отрезке [a,b];
б) имеет производную
во всех внутренних точках (a,b);
в) принимает наибольшее или
наименьшее значение
во внутренней точке c є (a,b).
Тогда :
Теорема Ролля.
Пусть функция
удовлетворяет условиям:
Теорема Лагранжа.
Пусть функция
удовлетворяет условиям:
а) непрерывна на отрезке [a,b];
б) имеет производную
во всех внутренних точках (a,b);
в) в концах отрезка принимает
одинаковые значения
Слайд 8
Исследование функций
Теорема Ферма.
Пусть функция
удовлетворяет условиям:
а) непрерывна на отрезке [a,b];
б) имеет производную
во всех внутренних точках (a,b);
в) принимает наибольшее или
наименьшее значение
во внутренней точке c є (a,b).
Тогда :
Теорема Ролля.
Пусть функция
удовлетворяет условиям:
Теорема Лагранжа.
Пусть функция
удовлетворяет условиям:
а) непрерывна на отрезке [a,b];
б) имеет производную
во всех внутренних точках (a,b);
в) в концах отрезка принимает
одинаковые значения
Тогда :
хотя бы в одной внутренней
точке c є (a,b).
Слайд 9
Исследование функций
Теорема Ферма.
Пусть функция
удовлетворяет условиям:
а) непрерывна на отрезке [a,b];
б) имеет производную
во всех внутренних точках (a,b);
в) принимает наибольшее или
наименьшее значение
во внутренней точке c є (a,b).
Тогда :
Теорема Ролля.
Пусть функция
удовлетворяет условиям:
Теорема Лагранжа.
Пусть функция
удовлетворяет условиям:
а) непрерывна на отрезке [a,b];
б) имеет производную
во всех внутренних точках (a,b);
в) в концах отрезка принимает
одинаковые значения
Тогда :
хотя бы в одной внутренней
точке c є (a,b).
а) непрерывна на отрезке [a,b];
б) имеет производную
во всех внутренних точках (a,b);
Слайд 10
Исследование функций
Теорема Ферма.
Пусть функция
удовлетворяет условиям:
а) непрерывна на отрезке [a,b];
б) имеет производную
во всех внутренних точках (a,b);
в) принимает наибольшее или
наименьшее значение
во внутренней точке c є (a,b).
Тогда :
Теорема Ролля.
Пусть функция
удовлетворяет условиям:
Теорема Лагранжа.
Пусть функция
удовлетворяет условиям:
а) непрерывна на отрезке [a,b];
б) имеет производную
во всех внутренних точках (a,b);
в) в концах отрезка принимает
одинаковые значения
Тогда :
хотя бы в одной внутренней
точке c є (a,b).
а) непрерывна на отрезке [a,b];
б) имеет производную
во всех внутренних точках (a,b);
Тогда :
хотя бы в одной внутренней
точке c є (a,b).
Слайд 11
Исследование функций
Теорема Ферма.
Пусть функция
удовлетворяет условиям:
а) непрерывна на отрезке [a,b];
б) имеет производную
во всех внутренних точках (a,b);
в) принимает наибольшее или
наименьшее значение
во внутренней точке c є (a,b).
Тогда :
Геометрический смысл.
Теорема Ролля.
Пусть функция
удовлетворяет условиям:
Теорема Лагранжа.
Пусть функция
удовлетворяет условиям:
а) непрерывна на отрезке [a,b];
б) имеет производную
во всех внутренних точках (a,b);
в) в концах отрезка принимает
одинаковые значения
Тогда :
хотя бы в одной внутренней
точке c є (a,b).
а) непрерывна на отрезке [a,b];
б) имеет производную
во всех внутренних точках (a,b);
Тогда :
хотя бы в одной внутренней
точке c є (a,b).
0
y
x
a
b
c
Слайд 12
Исследование функций
Теорема Ферма.
Пусть функция
удовлетворяет условиям:
а) непрерывна на отрезке [a,b];
б) имеет производную
во всех внутренних точках (a,b);
в) принимает наибольшее или
наименьшее значение
во внутренней точке c є (a,b).
Тогда :
Геометрический смысл.
Теорема Ролля.
Пусть функция
удовлетворяет условиям:
Теорема Лагранжа.
Пусть функция
удовлетворяет условиям:
а) непрерывна на отрезке [a,b];
б) имеет производную
во всех внутренних точках (a,b);
в) в концах отрезка принимает
одинаковые значения
Тогда :
хотя бы в одной внутренней
точке c є (a,b).
а) непрерывна на отрезке [a,b];
б) имеет производную
во всех внутренних точках (a,b);
Тогда :
хотя бы в одной внутренней
точке c є (a,b).
Геометрический смысл.
0
0
y
y
x
x
a
b
c
a
b
c
Слайд 13
Исследование функций
Теорема Ферма.
Пусть функция
удовлетворяет условиям:
а) непрерывна на отрезке [a,b];
б) имеет производную
во всех внутренних точках (a,b);
в) принимает наибольшее или
наименьшее значение
во внутренней точке c є (a,b).
Тогда :
Геометрический смысл.
Теорема Ролля.
Пусть функция
удовлетворяет условиям:
Теорема Лагранжа.
Пусть функция
удовлетворяет условиям:
а) непрерывна на отрезке [a,b];
б) имеет производную
во всех внутренних точках (a,b);
в) в концах отрезка принимает
одинаковые значения
Тогда :
хотя бы в одной внутренней
точке c є (a,b).
а) непрерывна на отрезке [a,b];
б) имеет производную
во всех внутренних точках (a,b);
Тогда :
хотя бы в одной внутренней
точке c є (a,b).
Геометрический смысл.
Геометрический смысл.
0
0
0
y
y
y
x
x
x
a
b
c
a
a
b
b
c
c
Слайд 14Исследование функций
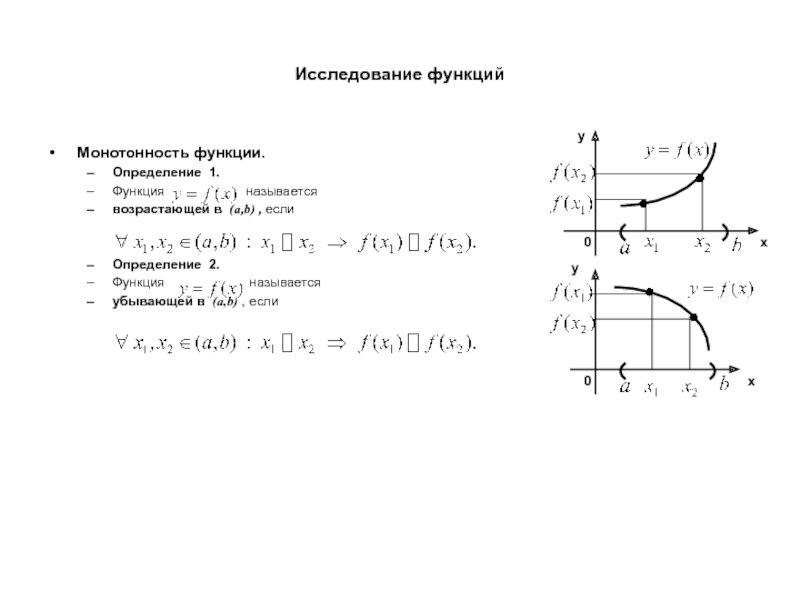
Монотонность функции.
Определение 1.
Функция
возрастающей в (a,b) , если
Определение 2.
Функция называется
убывающей в (a,b) , если
y
y
x
x
0
0
Слайд 16Исследование функций
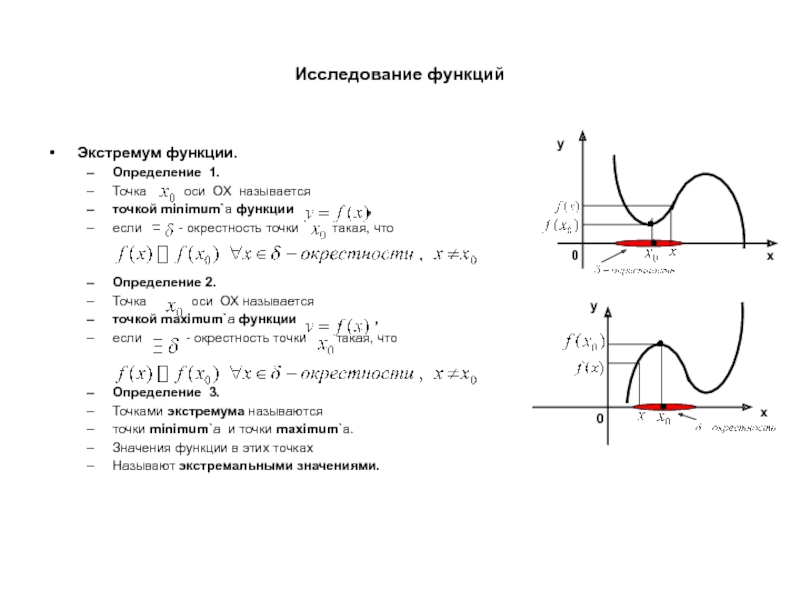
Экстремум функции.
Определение 1.
Точка оси ОХ называется
точкой minimum`а функции ,
если - окрестность точки такая, что
Определение 2.
Точка оси ОХ называется
точкой maximum`а функции ,
если - окрестность точки такая, что
Определение 3.
Точками экстремума называются
точки minimum`а и точки maximum`а.
Значения функции в этих точках
Называют экстремальными значениями.
y
y
x
x
0
0
Слайд 17Исследование функций
Необходимый признак экстремума.
Теорема.
1.
2.
Доказательство.
Пусть
Определение 3.
Критическими точками называются
точки оси ОХ , в которых
либо не существует.
Слайд 18Исследование функций
Достаточные признаки экстремума.
Определение.
Пусть
в δ - окрестности точки (включая точку ).
Пусть в δ - окрестности точки
(за исключением, быть может, точки ).
Говорят, что при переходе через точку
меняет знак с « + » на « - », если
Говорят, что при переходе через точку
меняет знак с « - » на « + » , если
Слайд 19Исследование функций
Первый достаточный признак экстремума.
Теорема.
1.
2.
3.
меняет знак с « + » на « - »
4. при переходе через точку
меняет знак с « - » на « + »
Доказательство.
1. меняет знак
с «+» на «-»
2. меняет знак
с «-» на «+»
Точка - точка maximum`а
Точка - точка minimum`а
Слайд 20Исследование функций
Второй достаточный признак экстремума.
Теорема.
1.
2.
3.
4.
Точка - точка minimum`а
Точка
Слайд 21Исследование функций
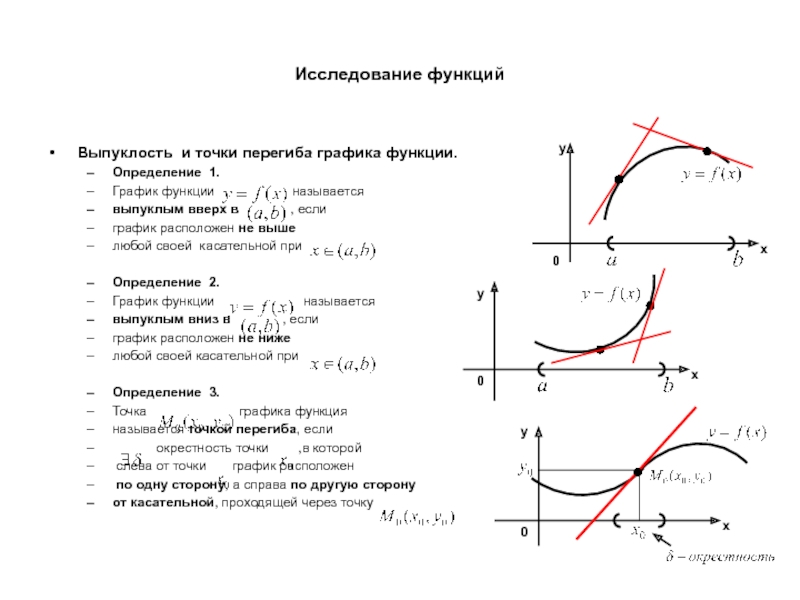
Выпуклость и точки перегиба графика функции.
Определение 1.
График функции
выпуклым вверх в , если
график расположен не выше
любой своей касательной при
Определение 2.
График функции называется
выпуклым вниз в , если
график расположен не ниже
любой своей касательной при
Определение 3.
Точка графика функция
называется точкой перегиба, если
окрестность точки ,в которой
слева от точки график расположен
по одну сторону, а справа по другую сторону
от касательной, проходящей через точку
y
y
y
x
x
x
0
0
0
Слайд 22Исследование функций
Достаточный признак выпуклости.
Теорема.
1.
2.
3.
График функции
выпуклый вниз в
График функции
выпуклый вверх в
Слайд 23Исследование функций
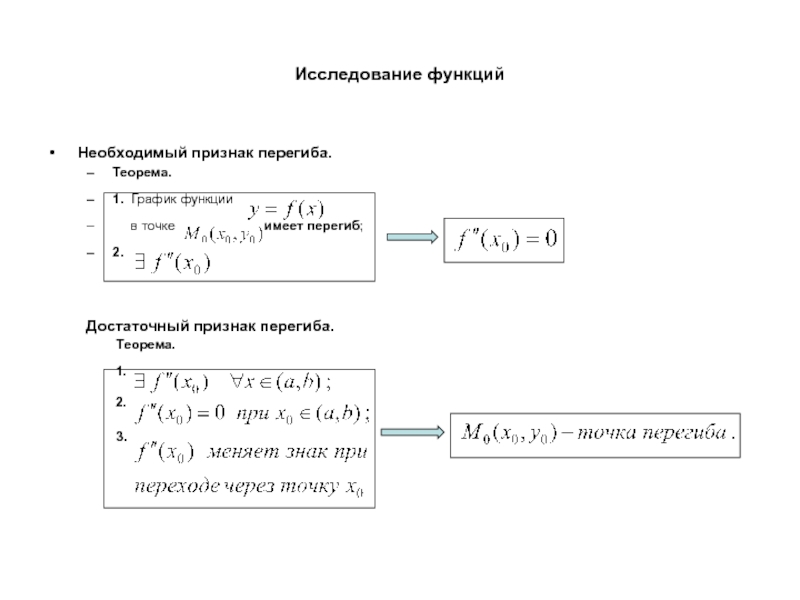
Необходимый признак перегиба.
Теорема.
1. График функции
в точке
2.
Достаточный признак перегиба.
Теорема.
1.
2.
3.
Слайд 24Исследование функций
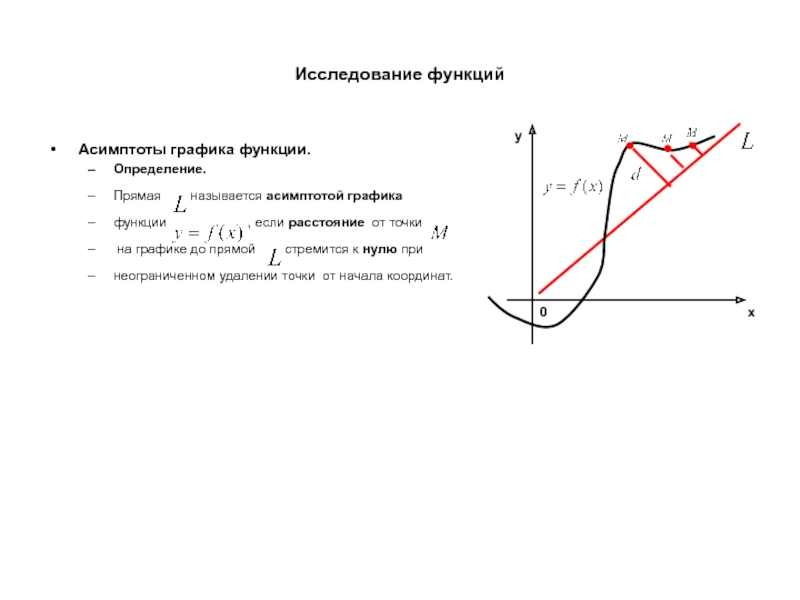
Асимптоты графика функции.
Определение.
Прямая называется асимптотой графика
функции
на графике до прямой стремится к нулю при
неограниченном удалении точки от начала координат.
0
x
y
Слайд 25Исследование функций
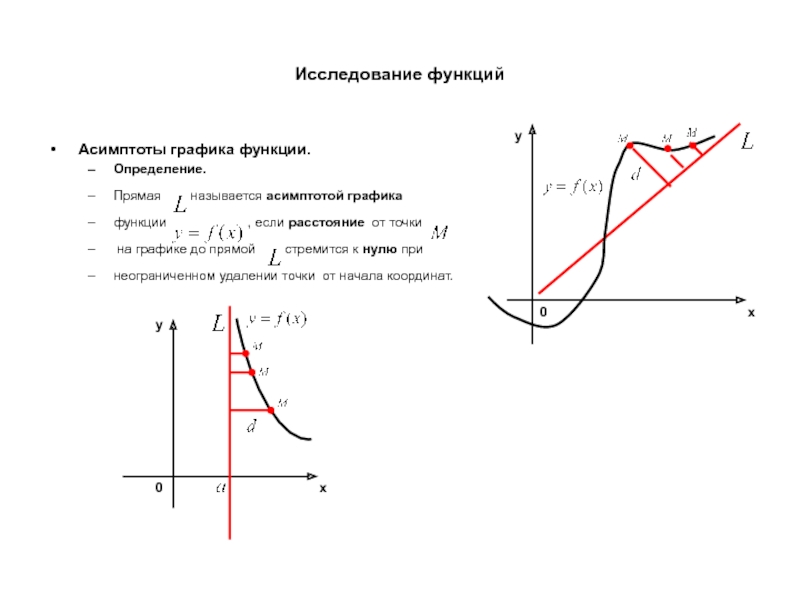
Асимптоты графика функции.
Определение.
Прямая называется асимптотой графика
функции
на графике до прямой стремится к нулю при
неограниченном удалении точки от начала координат.
0
x
y
0
x
y
Слайд 26Исследование функций
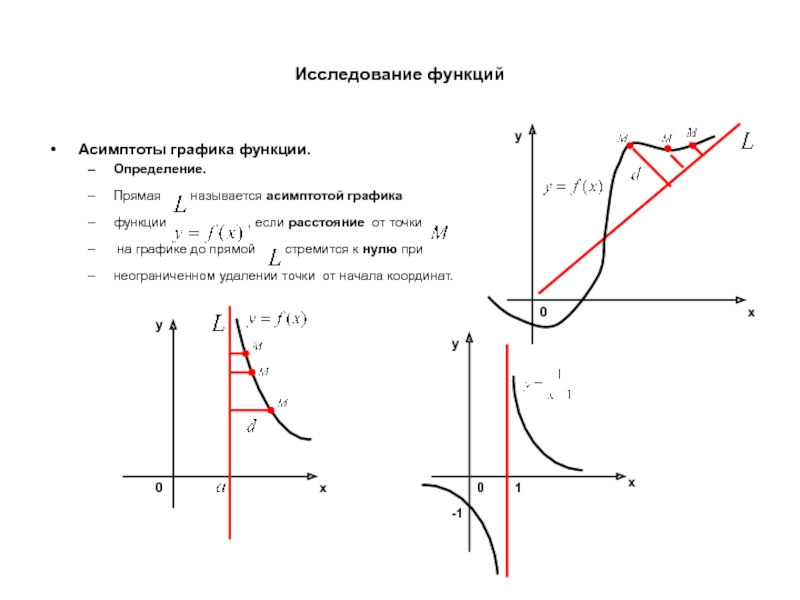
Асимптоты графика функции.
Определение.
Прямая называется асимптотой графика
функции
на графике до прямой стремится к нулю при
неограниченном удалении точки от начала координат.
0
x
y
0
0
x
x
y
y
1
-1
Слайд 27Исследование функций
Теорема 1.
Прямая является
если хотя бы один из пределов
равен
Теорема 2.
Прямая является наклонной асимптотой,
если
и
Замечание. Горизонтальная асимптота - частный случай
наклонной асимптоты при
Слайд 28Исследование функций
Общая схема исследования функции.
Первый этап.
1. Область определения, точки разрыва.
2. Четность,
3. Периодичность.
4. Точки пересечения с осями координат.
5. Асимптоты графика.
6. Поведение при
Уточненное исследование с помощью
первой производной.
1. Точки экстремума (вычислить экстремальные значения).
2. Интервалы монотонности.
Исследование с помощью второй производной.
1. Точки перегиба (вычислить значение функции и угловой коэффициент).
2. Интервалы выпуклости.
Слайд 29Исследование функций
Пример 1.
Исследовать функцию и построить график
1. О.О.Ф.
2. Четность, нечетность:
3. Непериодическая.
4.
с Оу:
С Ох:
Функция общего вида
Слайд 30Исследование функций
5. Асимптоты.
а) вертикальных асимптот нет;
б) наклонные:
6. Поведение при
Наклонных асимптот нет
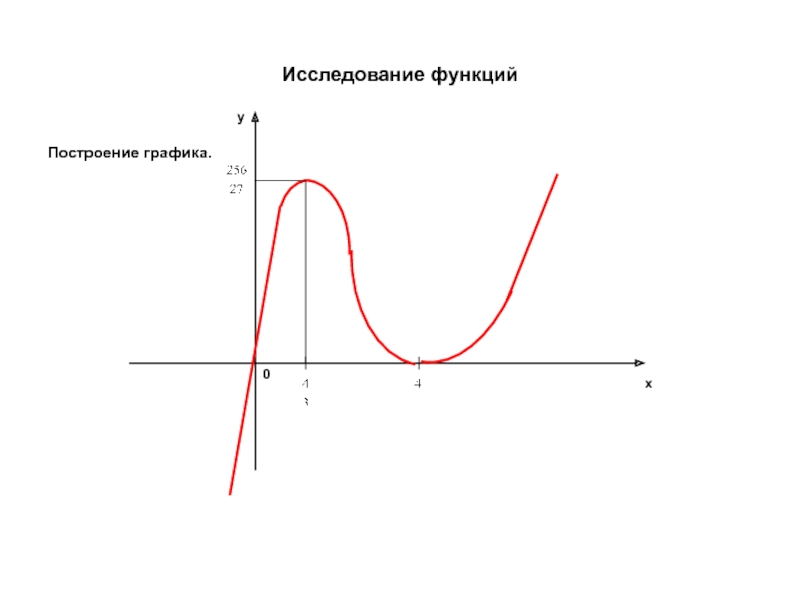
Слайд 35Исследование функций
Пример 2.
Исследовать функцию и построить график
1. О.О.Ф.:
2. Четность, нечетность:
3. Непериодическая.
4. Точки пересечения с осями координат:
5. Асимптоты:
а) вертикальные:
б) наклонные:
Функция
общего
вида.
