Презентации по Математике

Цифровые системы управления

м е д и а н а Отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны, называется биссектрисой треугольника. медиана биссектриса В Ы С О Т А

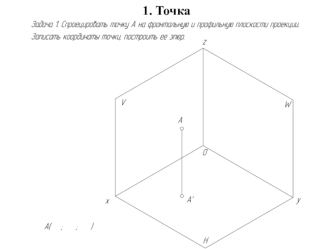
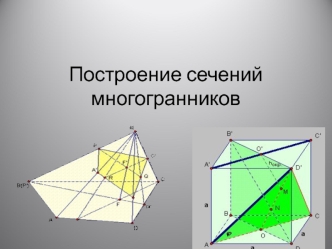
Содержание: Геометрические фигуры: Геометрические фигуры: точка, прямаяГеометрические фигуры: точка, прямая, Геометрические фигуры: точка, прямая, отрезок. Полуплоскость, луч и угол. Аксиомы и теоремы. Треугольники. Параллельные прямые. Смежные и вертикальные углы. Перпендикулярные прямые. Биссектриса угла. 1-ый и 2-ой признаки равенства треугольников. Высота,

Граф И ЕГО СВОЙСТВА ПРИМЕРЫ ГРАФОВ ЗАДАЧА: НАЙТИ КРАЙЧАЙШИЙ ПУТЬ. Решение. Дано: Иа-Иа (О) Винни-Пух (В) Пятачок (П) Кролик (К) Надо: Найти кратчайший путь

СИ (SI, фр. Le Système International d'Unités), (Система Интернациональная) — международная система единиц, современный вариант метрической систем.

23 +11

ЦЕЛЬ УРОКА: Сформировать навык в проведении опроса общественного мнения, представлении данных опроса в компактной табличной форме и наглядном изображении в форме диаграмм; Повторить действия с дробями. ПОВТОРЕНИЕ. ГЛАВЫ 8-9. Как называется число, стоящее над чертой дроби? Как называется число,

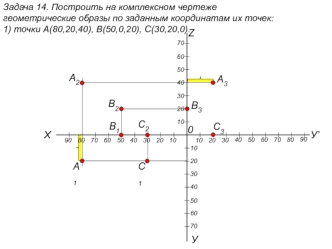
Прямая может принадлежать плоскости пересекать плоскость под некоторым углом пересекать плоскость под прямым углом (быть перпендикулярна плоскости) быть параллельна плоскости ПЛОСКОСТЬ. ПОЗИЦИОННЫЕ И МЕТРИЧЕСКИЕ ЗАДАЧИ Точка принадлежит плоскости, если она лежит на прямой, принадлежащей этой плоскости

Задачи: 1. Найти и проанализировать научно-методическую литературу по теме работы. 2. Выяснить какие меры длины использовали наши предки в России и в других странах. 3. Перечислить современные меры длины. 4.Сделать вывод. Цель работы – перечислить и проанализировать меры длины существовавшие

Настоящая программа предусматривает наиболее полное развитие целостной математической составляющей картины мира, расширение возможностей учащихся по свободному выбору своего образовательного пути, раскрывает широкие горизонты для развития познавательных интересов учащихся и повышает их информированность в различных аспектах современного труда. Основная функция данного

Транспортная задача Может возникать в физике, экономике и т.д. На отдельные компоненты транспортной сети (сеть железнодорожных, автомобильных и т.д. путей; сеть трубопроводов и т.д.) наложены ограничения – их максимально допустимая нагрузка. Необходимо определить максимально возможное количество пассажиров, товара, продукта и т.д.,

Определения Список – структура данных, представляющая собой конечную последовательность элементов. Элемент списка: Данные Связь Односвязные списки Односвязный список – это список, у элементов которого существует связь, указывающая на следующий элемент списка ( односторонняя связь).

мода медиана унимодальное и бимодальное распределения взвешенное среднее моменты распределения асимметрия (skewness) эксцесс ЗР исчерпывающе описывают СВ и позволяют рассчитать вероятности любых связанных с ними событий Однако: 1) Не всегда необходимы

Процедура оценивания Берется выборка из n наблюдений и с помощью подходящей формулы рассчитывается оценка нужной характеристики. Нужно следить за терминами, делая важное различие между способом или формулой оценивания и рассчитанным по ней для данной выборки числом, являющимся значением оценки. Способ

МОСКВА, 2009 ООО "РЕЗОЛЬВЕНТА" СЛАЙД-ЛЕКЦИЯ № 1 ТЕМА ЛЕКЦИИ: «МАТРИЦЫ И ДЕЙСТВИЯ НАД НИМИ» МОСКВА, 2009 ООО "РЕЗОЛЬВЕНТА" ПЛАН ЛЕКЦИИ 1. ПОНЯТИЕ И ВИДЫ МАТРИЦ 2. СТРОКИ, СТОЛБЦЫ, ЭЛЕМЕНТЫ И РАЗМЕР МАТРИЦ

Определение марковского процесса 29.09.2014 Марковские процессы Однородный МП 29.09.2014 Марковские процессы

Определение сечения. Секущей плоскостью многогранника назовем любую плоскость, по обе стороны от которой имеются точки данного многогранника. Секущая плоскость пересекает грани многогранника по отрезкам. Многоугольник, сторонами которого являются эти отрезки,

Цель проекта 1).Изучить и исследовать числа, которые связаны с историей и фактами нашего полуострова;   2). Развить логические навыки и

Задача 14. Построить на комплексном чертеже геометрические образы по заданным координатам их точек: 2) прямую: а(А,В): А(80,30,40), В(20,30,40) Х У У’ 0 A1 Z A2 А3 B1 B2 ≡В3 a1 a2 Вывод: Прямая

План Введение: управление рисками и задачи моделирования Построение модели Байесовская вероятность Принцип построения Байесовской сети Использование сети для управления рисками АП Вопросы для самопроверки Руководящие документы Руководство по управлению

Жоспары: Вектор шамалар ұғымы. Оларды қосу, алу, санға көбейту. Векторлардың скаляр көбейтіндісі. Векторлардың вектор көбейтіндісі. Векторларды қосу a және b векторларының a+b қосындысын параллелограмм ережесі бойынша есептеуге болады. Бұл үшін бұл векторларды сызайық: a+b қосындысын

Функция 1   1)Область определения функции.  

Определение Функция y=f (x) называется чётной, если: D (f) симметрична относительно нуля; 2) для любого х Є D (f) верно равенство: f (-x) = f (x). Функция y=f (x) называется нечётной, если: 1) D (f) симметрична относительно нуля; 2)