- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Связь между переменными состояния и переменными вход-выход презентация
Содержание
- 1. Связь между переменными состояния и переменными вход-выход
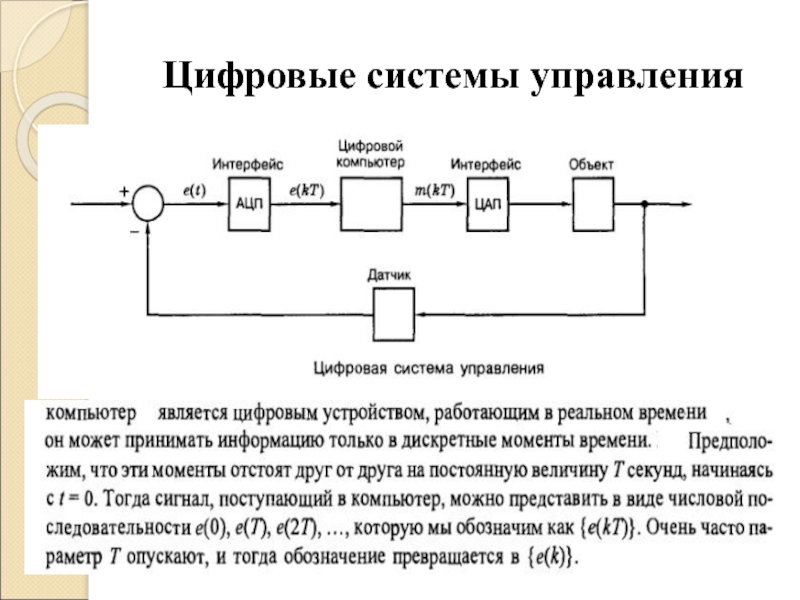
- 3. Цифровые системы управления
- 4. Разностные уравнения
- 6. Связь ДУ и разностных уравнений
- 8. Оптимальное управление и вариационное исчисление С точки
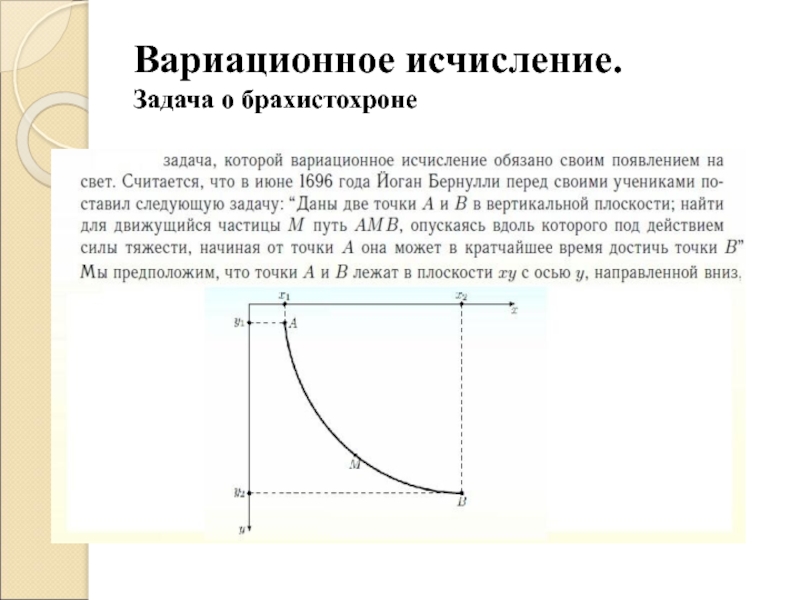
- 9. Вариационное исчисление. Задача о брахистохроне
- 10. Задача о брахистохроне-2
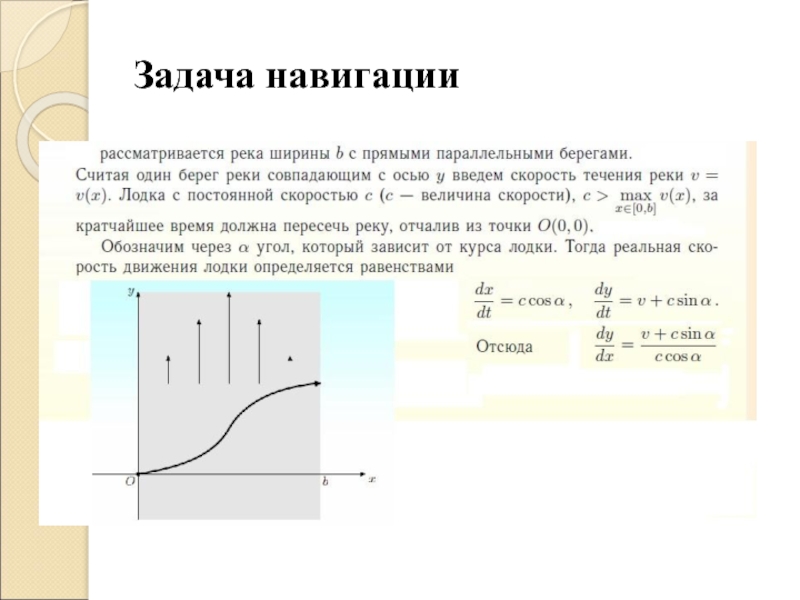
- 11. Задача навигации
- 12. Задача навигации-2
- 13. Простейшие задачи вариационного исчисления MIN
- 14. Уравнение Эйлера-Лагранжа
- 15. Пример решения простейшей вариационной задачи Решение
- 16. Пример решения простейшей вариационной задачи-2
- 17. Обобщения простейшей задачи вариационного исчисления
- 18. Пример
- 19. Обобщения простейшей задачи вариационного исчисления -2
- 20. Пример
- 21. Изопериметрические задачи
- 22. Пример
- 24. Задачи оптимального управления
- 25. Задачи оптимального управления-2
- 26. Решение задач оптимального управления на основе вариационного исчисления
- 27. Решение задач оптимального управления на основе вариационного исчисления
- 28. ПРИМЕР
- 29. ПРИМЕР(окончание)
- 30. Z-преобразование (дискретное преобразование Лапласа)
- 32. Свойства Z-преобразования Аналогичны свойствам преобразования Лапласа(самостоятельно)
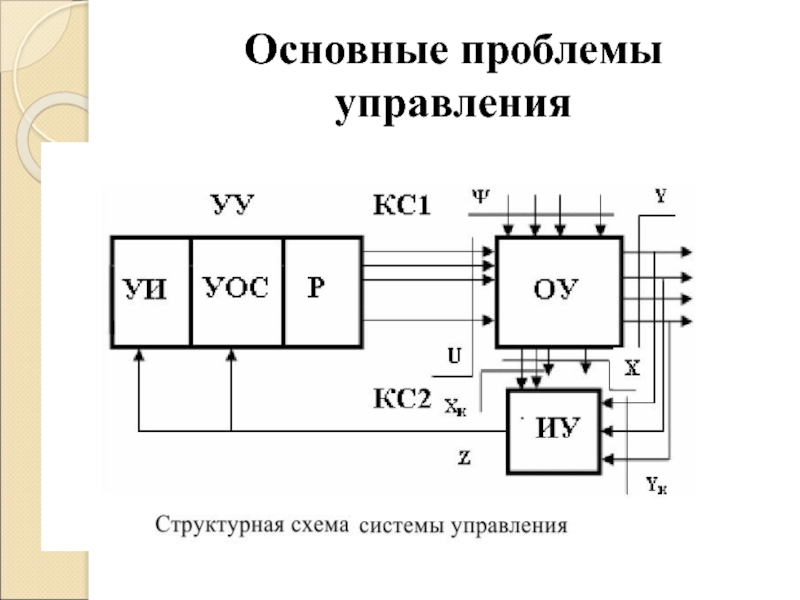
- 33. Основные проблемы управления
- 34. Части системы управления ОУ – объект управления,
- 35. Части системы управления-1 УИ – устройство идентификации
Слайд 8Оптимальное управление и вариационное исчисление
С точки зрения математики задача оптимального управления
представляет собой задачу нахождения экстремума функционала(функция, аргументом которой есть функция), которая рассматривается в вариационном исчислении.
Она сходна с задачей нахождения экстремума функции многих переменных в математическом анализе, когда необходимые условия, которым должны удовлетворять независимые переменные скалярной функции, определяются приравниванием нулю всех частных производных функций по своим аргументам.
При минимизации функционала получается не система алгебраических уравнений, которым удовлетворяют независимые переменные в точке экстремума скалярной функции, а система дифференциальных уравнений, которым на интервале управления удовлетворяют так называемые экстремали, являющиеся функциями времени.
Процедура нахождения экстремума функционала усложняется из-за необходимости удовлетворять ограничениям, налагаемым на переменные управлений и состояний.
Ограничения учитывают, используя метод множителей Лагранжа.
Она сходна с задачей нахождения экстремума функции многих переменных в математическом анализе, когда необходимые условия, которым должны удовлетворять независимые переменные скалярной функции, определяются приравниванием нулю всех частных производных функций по своим аргументам.
При минимизации функционала получается не система алгебраических уравнений, которым удовлетворяют независимые переменные в точке экстремума скалярной функции, а система дифференциальных уравнений, которым на интервале управления удовлетворяют так называемые экстремали, являющиеся функциями времени.
Процедура нахождения экстремума функционала усложняется из-за необходимости удовлетворять ограничениям, налагаемым на переменные управлений и состояний.
Ограничения учитывают, используя метод множителей Лагранжа.
Слайд 34Части системы управления
ОУ – объект управления, представляющий собой
некоторый физический объект
(технологический процесс), на котором размещены
регулирующие органы (РО), управляемые сформированны-
ми по некоторому закону сигналами управления;
ИУ – измерительное устройство, преобразующее доступные непосредственному измерению компоненты вектора состояния и вектора выхода в электрический сигнал, согласованный с предоставленным каналом связи (КС);
регулирующие органы (РО), управляемые сформированны-
ми по некоторому закону сигналами управления;
ИУ – измерительное устройство, преобразующее доступные непосредственному измерению компоненты вектора состояния и вектора выхода в электрический сигнал, согласованный с предоставленным каналом связи (КС);
Слайд 35Части системы управления-1
УИ – устройство идентификации объекта управления;
УОС – устройство
оценивания состояния объекта управления; Р – регулятор, представляющий собой техническую среду, средствами которой создается сигнал управления U, сформированный в соответствии с требуемым закон управления
(ЗУ) регулирующими органами ОУ;
УУ – устройство управления,представляющее собой функциональное объединение устройства идентификации объекта, устройства оценивания его состояния и регулятора;
КС1, КС2 – соответственно прямой (управляющий) и обратный (информационный, известительный) каналы связи.
(ЗУ) регулирующими органами ОУ;
УУ – устройство управления,представляющее собой функциональное объединение устройства идентификации объекта, устройства оценивания его состояния и регулятора;
КС1, КС2 – соответственно прямой (управляющий) и обратный (информационный, известительный) каналы связи.