Презентации по Математике

№99565. В 2008 году в городском квартале проживало 40000 человек. В 2009 году, в результате строительства новых домов, число жителей выросло на 8%, а в 2010 году − на 9% по сравнению с 2009 годом. Сколько человек стало проживать в квартале

Цели: Цели урока: ввести понятие перпендикуляра к прямой, медианы, биссектрисы и высоты треугольника; доказать теорему о перпендикуляре; учитьcя строить медианы, биссектрисы и высоты треугольника. Вспомним!

“Конуси” оточують нас Конічна поверхня m M Пряма m, що проходить через точку М, рухаючись вздовж замкненої кривої (L) описує конічну поверхню. Пряма, яка утворює конічну поверхню, називається твірною. Якщо замкнена крива має форму круга, то ми отримуємо

МИНИМАЛЬНАЯ БАЗА РЕБЕР Содержательная постановка задачи: на связном взвешенном неориентированном графе G(X,U) выделить подмножество ребер таких, что: 1. Граф G(X,U’) является связным. 2. Суммарный

ЧИСЛА В ЗАГАДКАХ Единица, один, первый 1. Стоит Антошка на одной ножке; его ищут, а он не откликается. 2. На ноге стоит одной, крутит-вертит головой. Нам показывает страны, реки, горы, океаны .

2-я ц. 3-я ц. 1-я ц. а) 1 9 чисел 2-я ц. 3-я ц. 1-я ц. а) 3 еще 9 чисел и т.д. Ответ: 27 чисел

План 7.1 Постановка задачі нелінійного програмування; основні труднощі в задачах нелінійного програмування. 7.2 Графічний метод: задача з лінійною цільовою функцією й нелінійною системою обмежень; задача з нелінійною цільовою функцією й лінійною системою обмежень; задача з нелінійною цільовою функцією й нелінійною

Задача 2 В кубе А…D1 найдите косинус угла между прямыми АВ и СА1. Задача 3 В правильной четырехугольной пирамиде SABCD, все ребра которой равны 1. Найдите синус угла между прямой BD и плоскостью (SBC). S

МЕТОДЫ ПЛАНИРОВАНИЯ И ОБРАБОТКИ РЕЗУЛЬТАТОВ ИНЖЕНЕРНОГО ЭКСПЕРИМЕНТА Спирин Н.А., Лавров В.В., Зайнуллин Л.А., Бондин А.Р., Бурыкин А.А. учебное пособие для студентов вузов, обучающихся по программам бакалавриата 22.03.02 и магистратуры 22.04.02 направления «Металлургия» / Уральский федеральный университет им. первого Президента России Б.Н.

Сравнение двух средних нормальных совокупностей, дисперсии которых неизвестны и одинаковы (малые независимые выборки). Принятие решений. Двусторонняя проверка. Если альтернативная гипотеза Н1: М(X)≠M(Y) То Если , то

В кубе A…D1 найдите угол между прямыми AC и BD1. Куб 1 В кубе A…D1 найдите угол между прямыми AE и BF1, где E и F1 – середины ребер соответственно BC и C1D1. Куб 2

Проблемный вопрос: Окружность и круг - это одна и та же фигура или нет ? На уроке я должен: получить представление об окружности и круге; получить представление об элементах окружности

5. Теорема запаздывания.

Три этапа математического моделирования: 1) составление математической модели; 3) ответ на вопрос задачи. 2) работа с математической моделью; составлением математической модели 1. 3. 2. работа с математической моделью

Геометрический способ решения игры(2x2) Варианты решений: 1 уравнение 2 уравнение Геометрическое решение игры (2xN) и (Mx2)

Логика высказываний оперирует простейшими высказываниями, которые могут быть или истинными, или ложными. В разговорном языке встречаются более сложные повествовательные предложения, истинность которых может меняться при изменении объектов, о которых идет речь. В логике такие предложения,

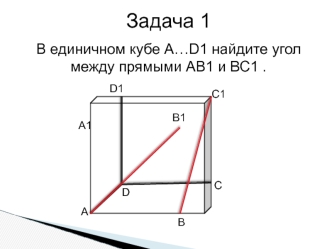
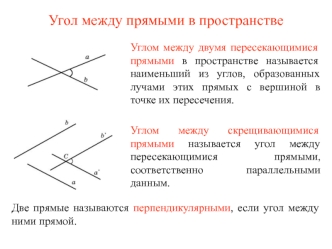
Данная тема актуальна, так как подобные задачи требуют развитого абстрактного мышления. Задачи, представленные ниже, чаще всего вызывают затруднения при решении у учащихся. Наглядное решение позволяет лучше усвоить приемы решения таких задач. Нахождение угла между скрещивающимися прямыми и угла между

Определение. Схемой Бернулли называется последовательность независимых испытаний, в каждом из которых возможны лишь два исхода —«успех» и «неудача», при этом «успех» в одном испытании происходит с вероятностью p, «неудача» — с вероятностью q =1- p. Теорема. (Формула Бернулли). Доказательство. Событие

Цілі і задачі статистичної перевірки гіпотез Математичний апарат статистичної перевірки гіпотез використовують для аналізу значущості отриманих вибіркових числових характеристик для генеральних сукупностей. Наприклад, можна відповісти на питання про те, чи є значущим знайдене вибіркове середнє і

Цель нашего урока целеполагание Мы продолжаем записывать дробные числа по-новому. Но не ко всем обыкновенным дробям можно применить новую запись. Кто-нибудь догадался, к каким? Эти дроби перед вами. Полюбуйтесь ими сами. В знаменателе, смотри – Единица и нули.  

Дана прямая в пространстве, на ней взята точка. Сколько можно построить прямых, проходящих через эту точку и перпендикулярных данной прямой? Ответ: Бесконечно много. Упражнение 1 Даны прямая и точка вне ее. Сколько можно построить прямых, проходящих через эту точку и

Определение Случайная величина – это переменная, которая в результате эксперимента принимает одно из своих возможных значений, причем заранее не известно какое именно. Случайные величины обозначается заглавными буквами латинского алфавита, соответствующие числовые значения - строчными Дискретные и непрерывные случайные величины