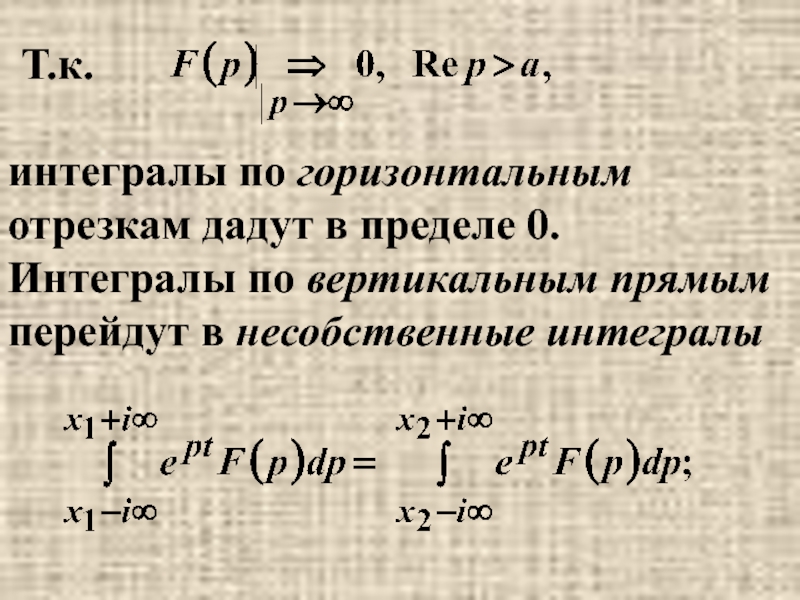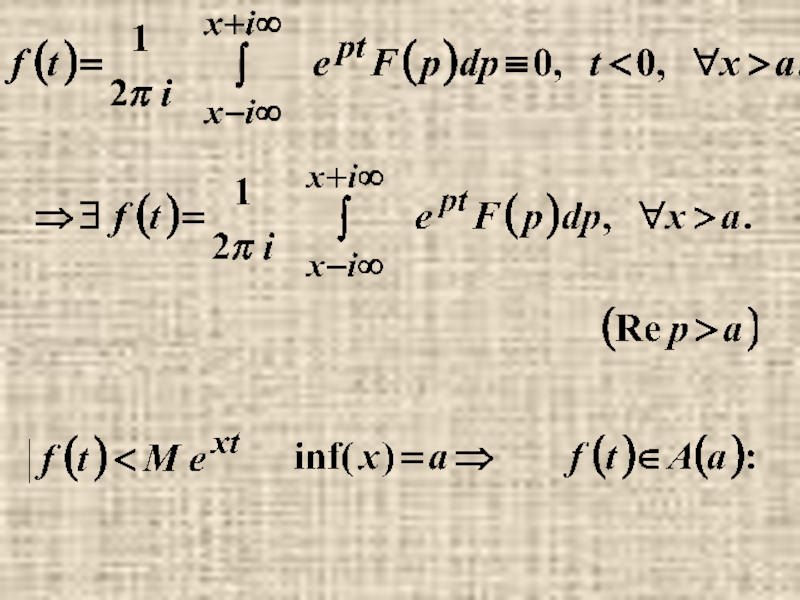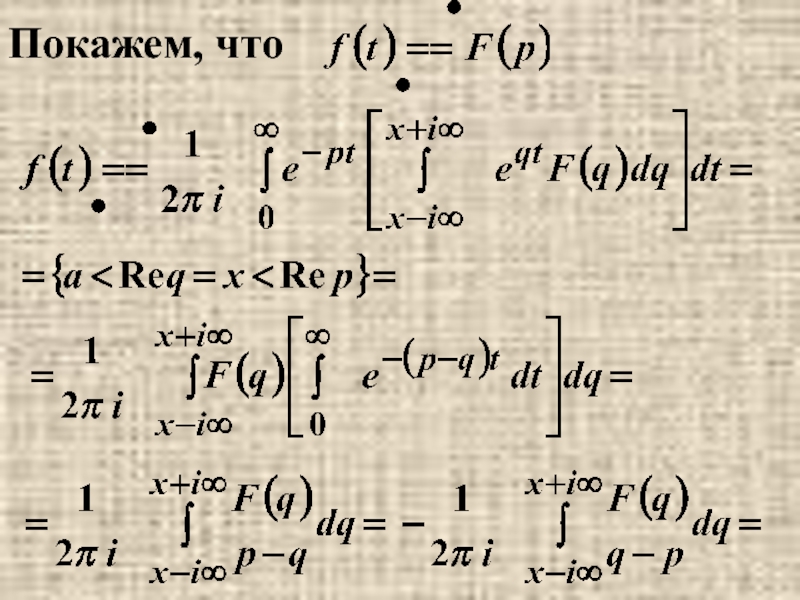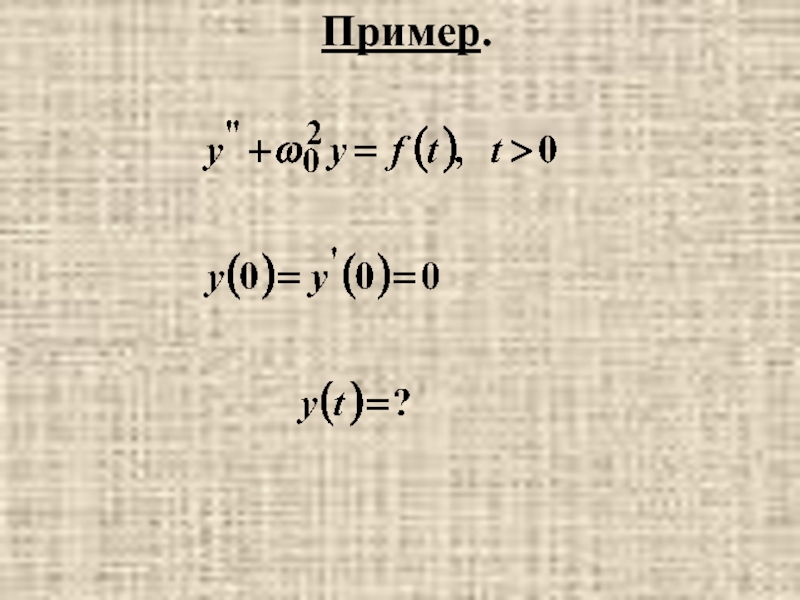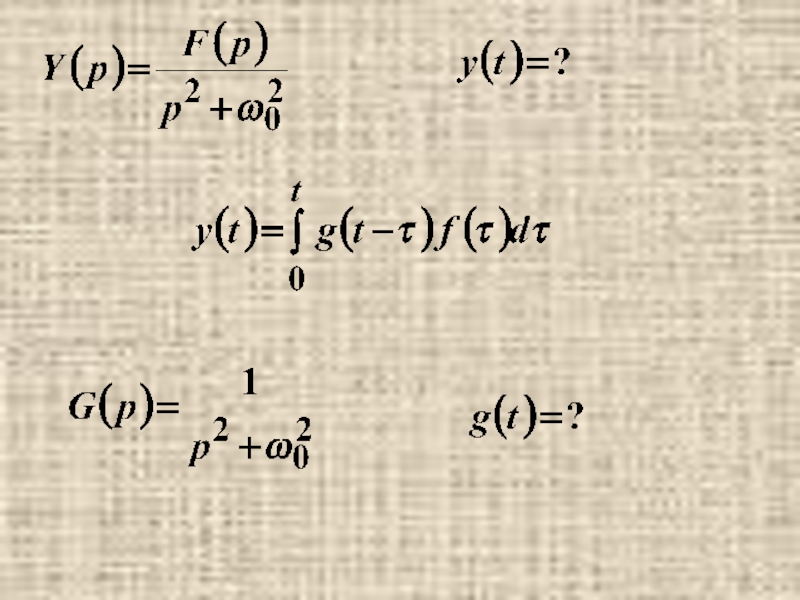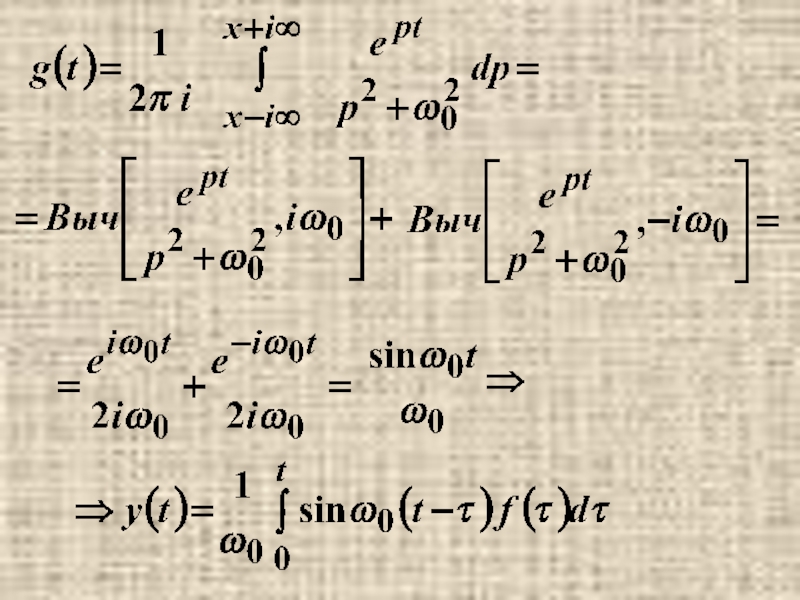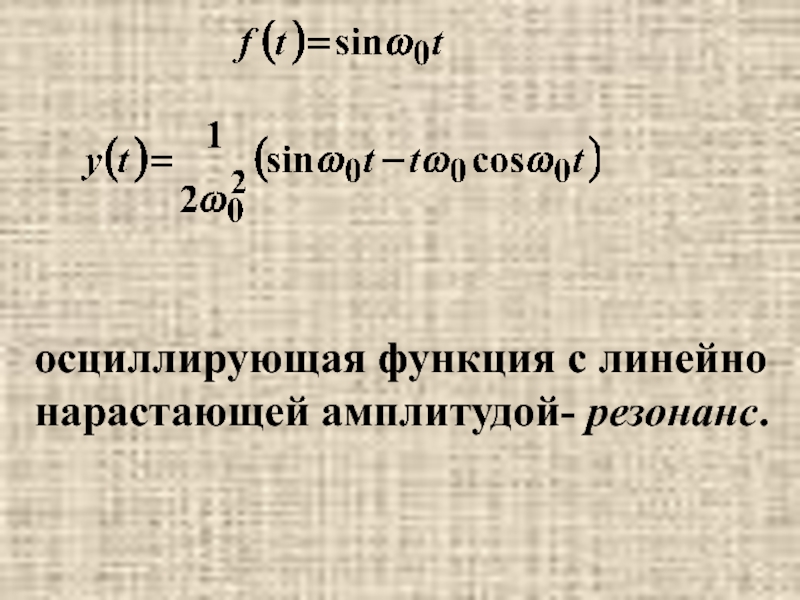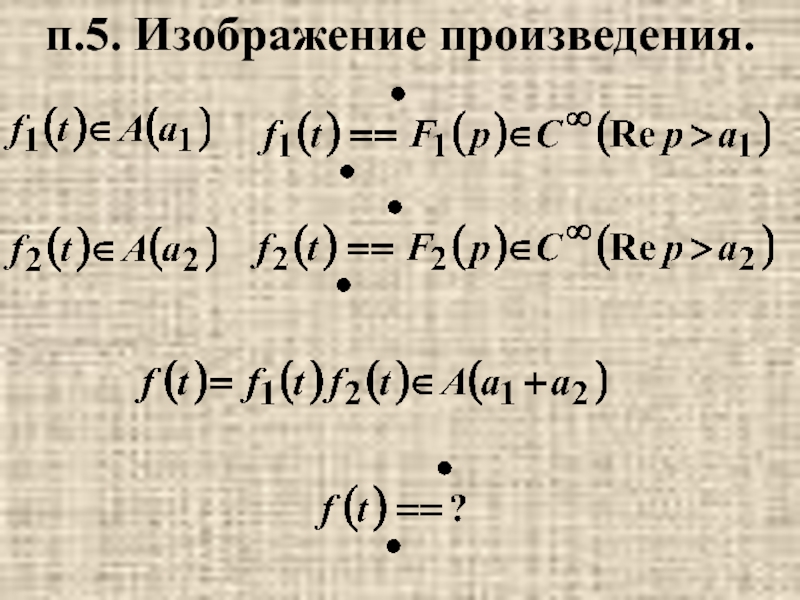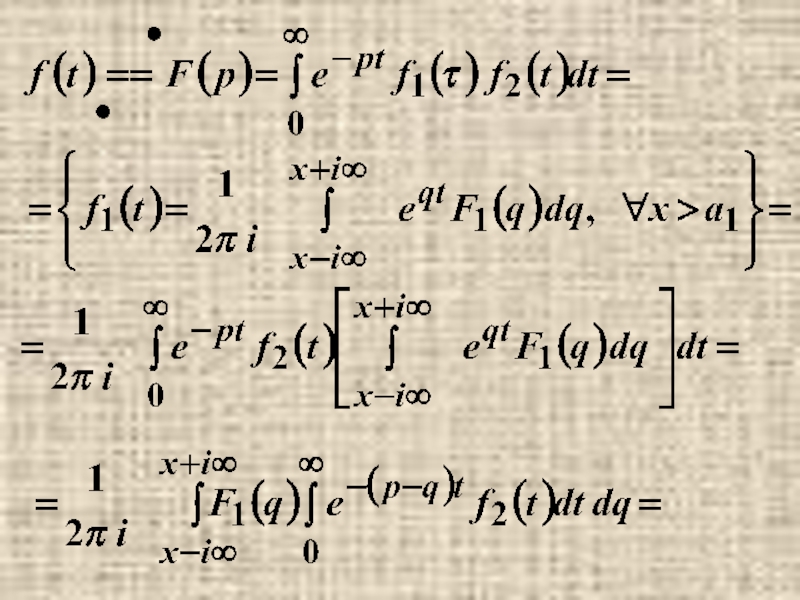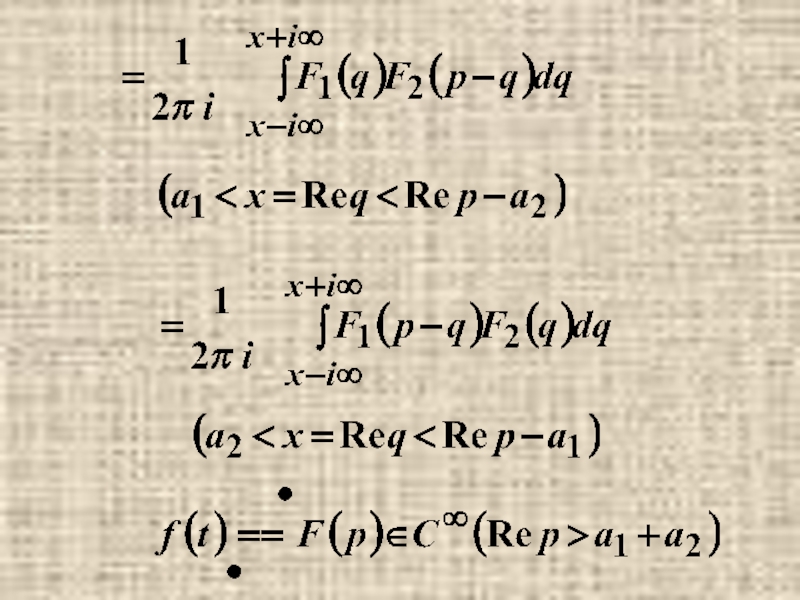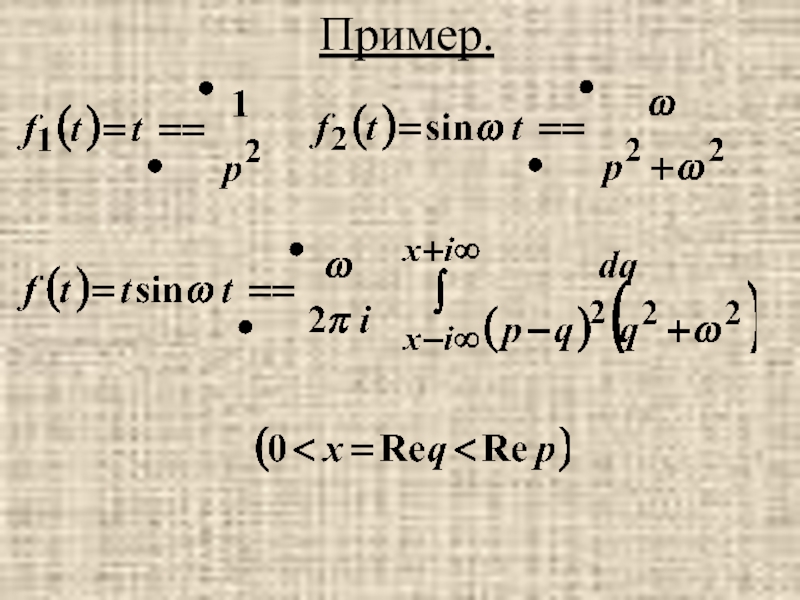- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Линейность изображений презентация
Содержание
- 1. Линейность изображений
- 3. 5. Теорема запаздывания.
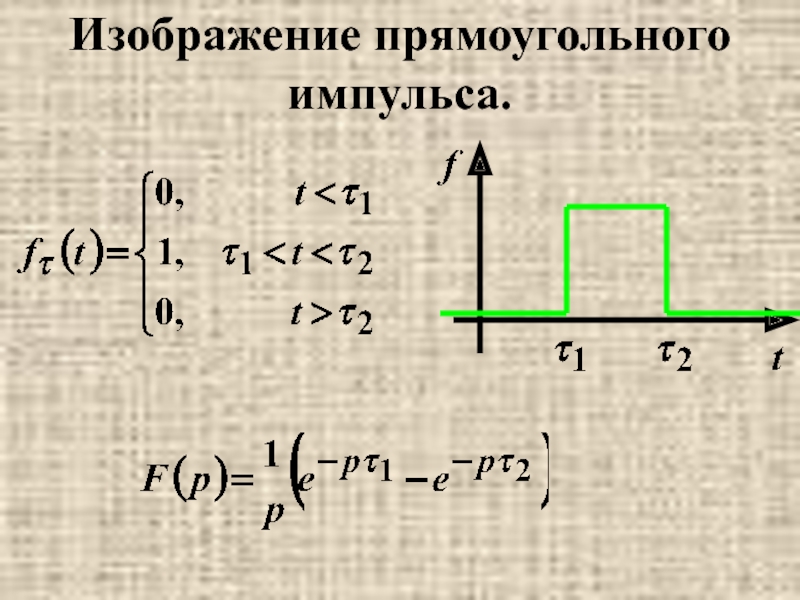
- 5. Изображение прямоугольного импульса.
- 6. 6. Изображение производной
- 7. (по частям)=
- 8. кусочно- непрерывная
- 10. 7. Изображение интеграла.
- 13. 8. Изображение свертки.
- 15. п.3. Решение задачи Коши для
- 17. Пусть
- 22. Интеграл Дюгамеля.
- 23. п.4. Теорема Меллина. Пусть и
- 24. Тогда
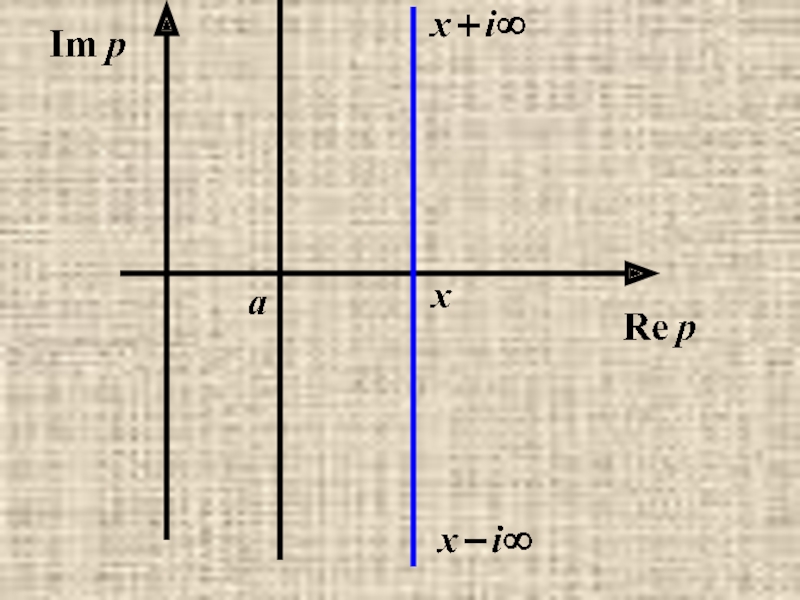
- 25. Замечание. Несобственный интеграл вычисляется вдоль прямой Re p=x>a и понимается в смысле главного значения:
- 27. Доказательство. Рассмотрим и докажем:
- 28. Замечание: на ∀ [0,T] интеграл сходится равномерно
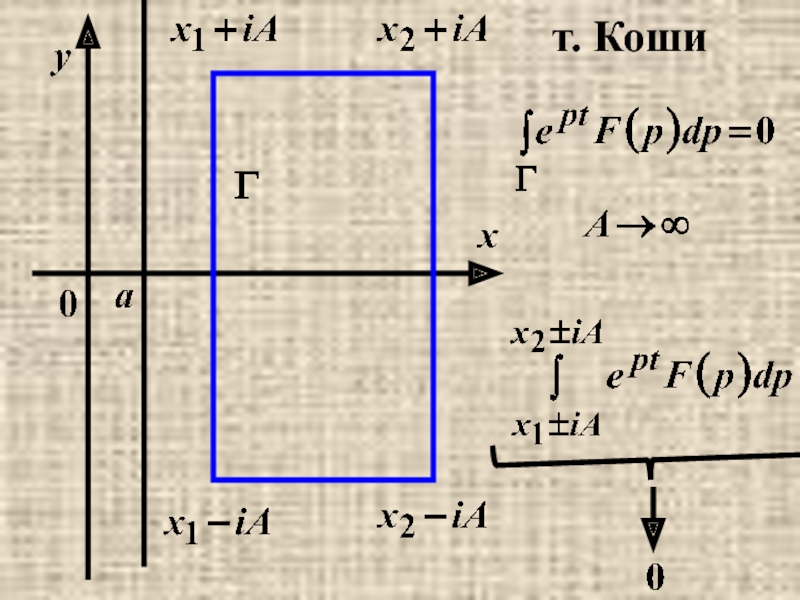
- 29. т. Коши
- 30. интегралы по горизонтальным отрезкам дадут в пределе
- 31. 3) Докажем, что I ( x ,
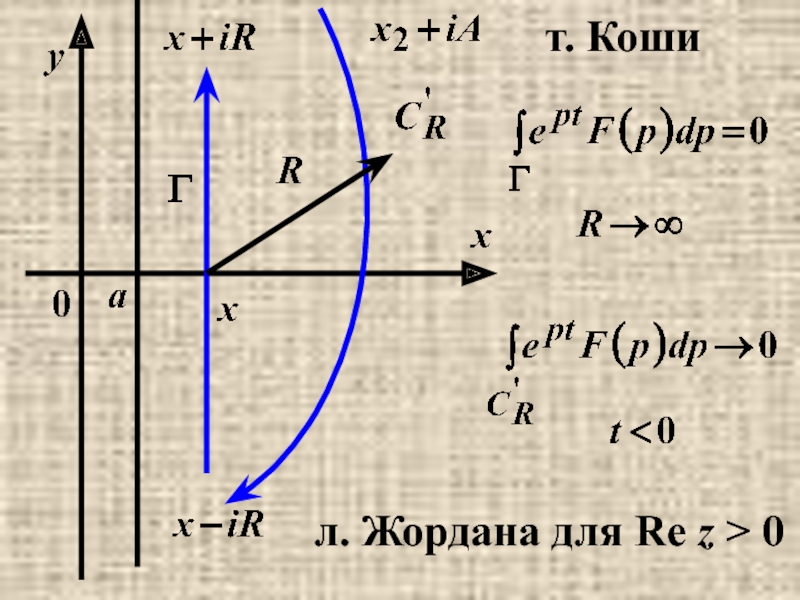
- 32. т. Коши л. Жордана для Re z > 0
- 34. Покажем, что
- 35. =(интеграл можно вычислить с помощью вычетов, учитывая,
- 36. Замечание. Если ∃ аналитическое продолжение F(p) в
- 37. В частности, если F(p)=1/Pn(p), где все нули полинома Pn(p) лежат в левой полуплоскости Re p
- 38. Пример.
- 41. осциллирующая функция с линейно нарастающей амплитудой- резонанс.
- 42. п.5. Изображение произведения.
- 45. Пример.
- 46. ={при помощи вычетов, с учетом того, что
- 47. Замечание. Можно считать контур интегрирования замкнутым налево и суммировать вычеты в ±iω;
Слайд 15п.3. Решение задачи Коши для линейного обыкновенного дифференциального уравнения с постоянными
коэффициентами
операционным методом.
Слайд 23п.4. Теорема Меллина.
Пусть
и
(равномерно относительно аргумента)
(равномерно ограничен по x
)
Слайд 25Замечание. Несобственный интеграл
вычисляется
вдоль прямой Re p=x>a и понимается в смысле
главного значения:
Слайд 28Замечание: на ∀ [0,T] интеграл сходится равномерно по t.
2) Покажем,
что I(x , t) не зависит от x при x > a.
Слайд 30интегралы по горизонтальным отрезкам дадут в пределе 0. Интегралы по вертикальным
прямым перейдут в несобственные интегралы
Слайд 35=(интеграл можно вычислить с помощью вычетов, учитывая, что контур обходится по
часовой стрелке “-”)=
Слайд 36Замечание. Если ∃ аналитическое продолжение F(p) в левую полуплоскость (Re p
a), имеющее конечное число N изолированных особых точек pn и удовлетворяющее условиям леммы Жордана, то
Слайд 37В частности, если F(p)=1/Pn(p), где все нули полинома Pn(p) лежат в
левой полуплоскости Re p
Слайд 46={при помощи вычетов, с учетом того, что контур интегрирования замыкается вправо
и обходится по часовой стрелке- в отрицательном направлении}=
{q=p- полюс 2-го порядка }

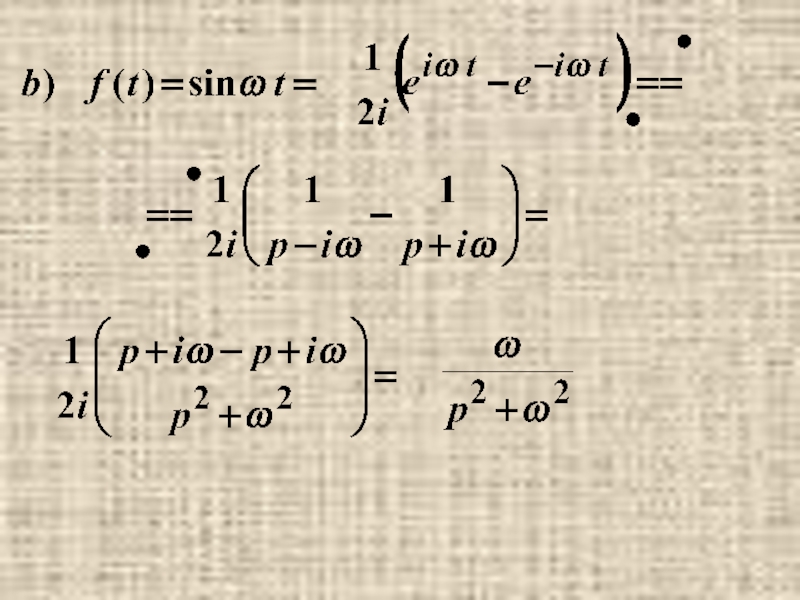

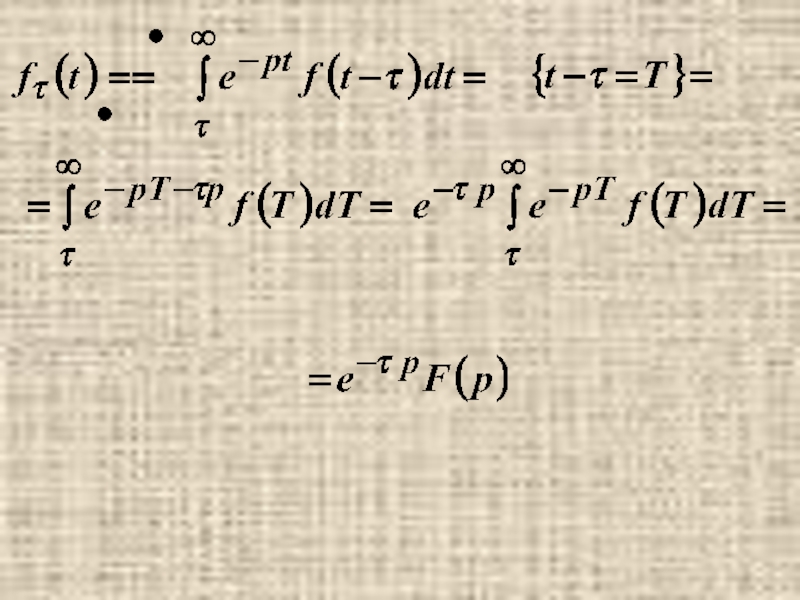

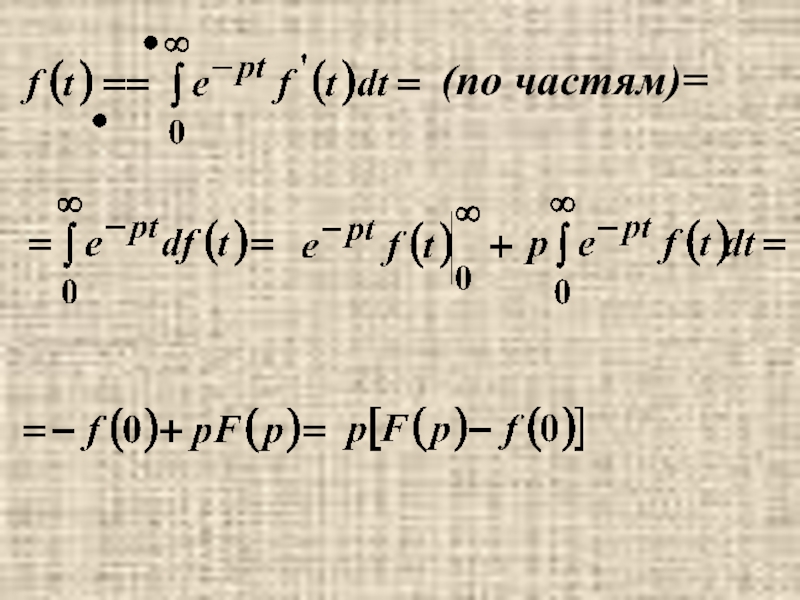
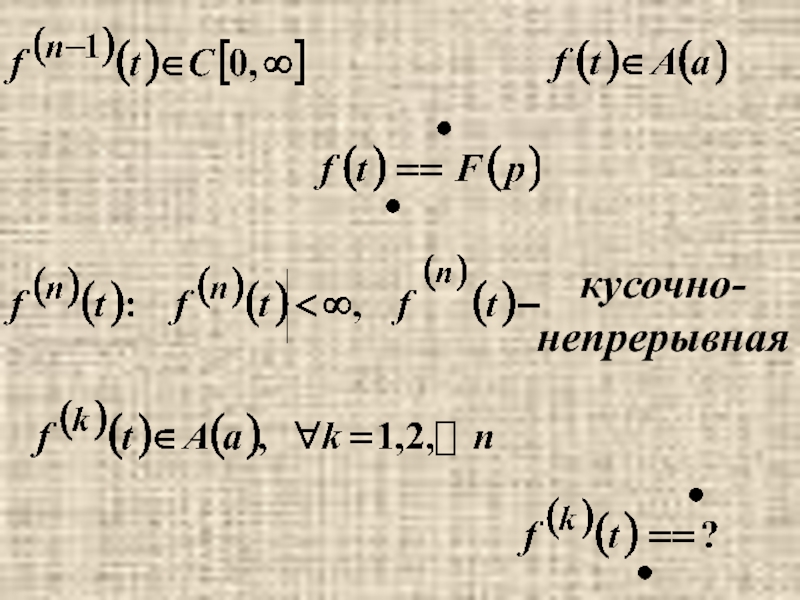
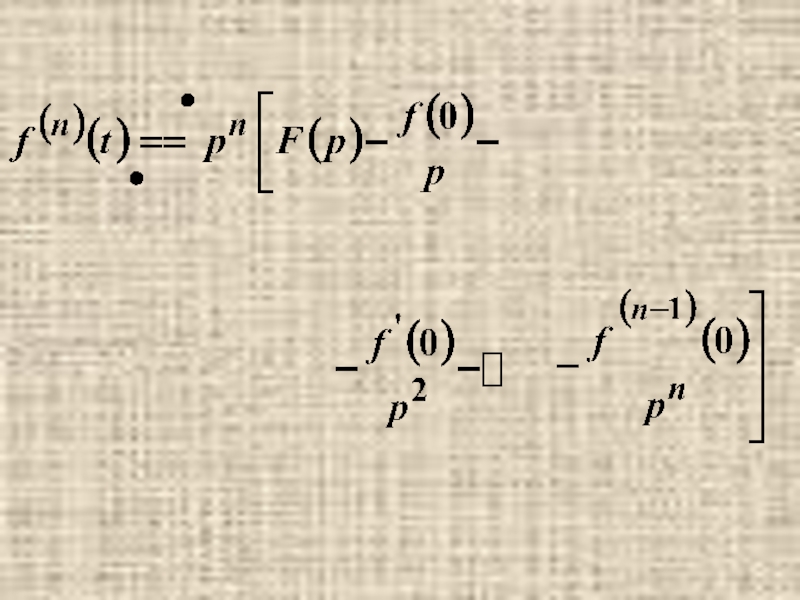
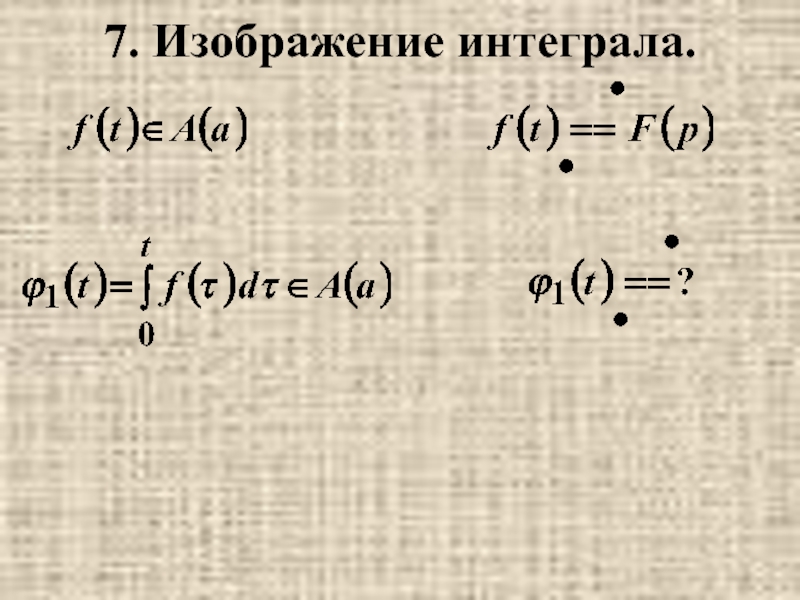
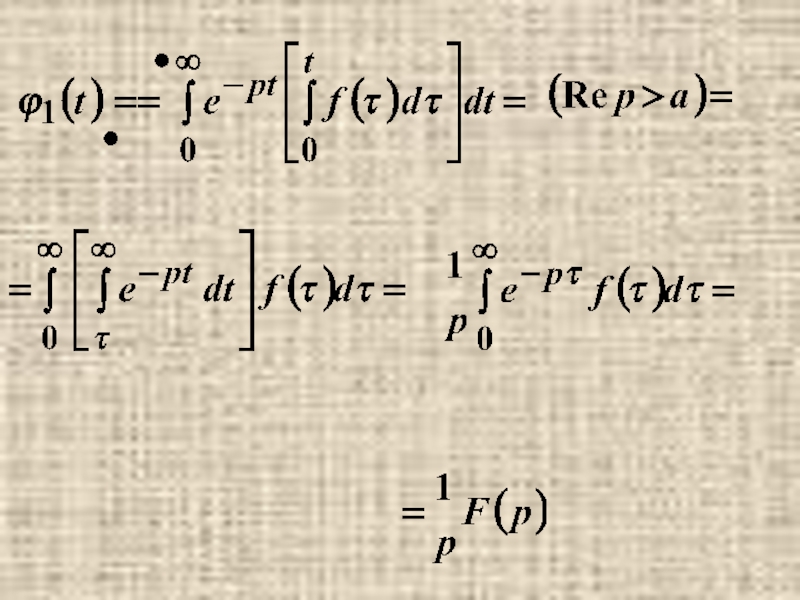
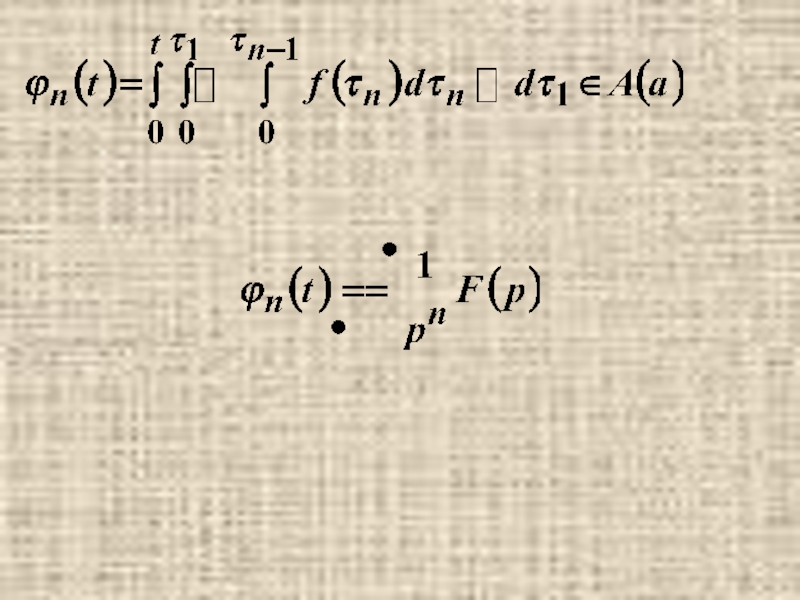
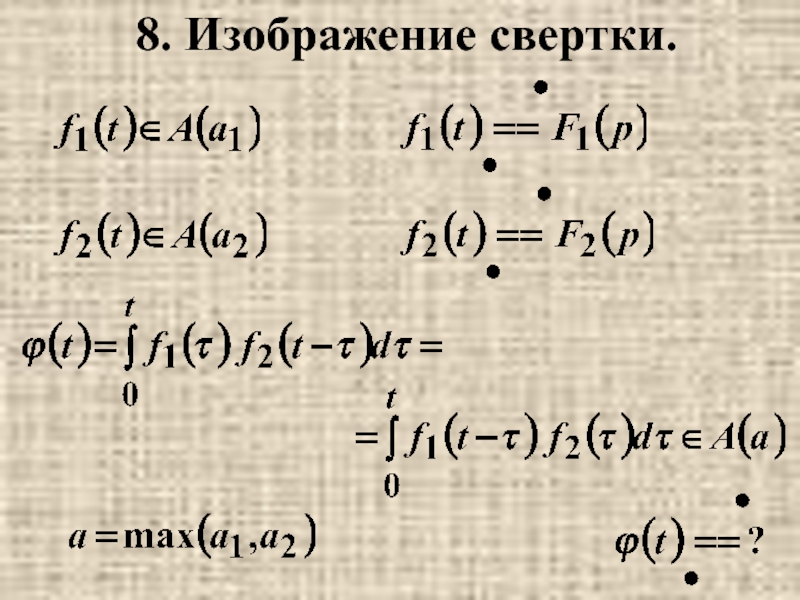
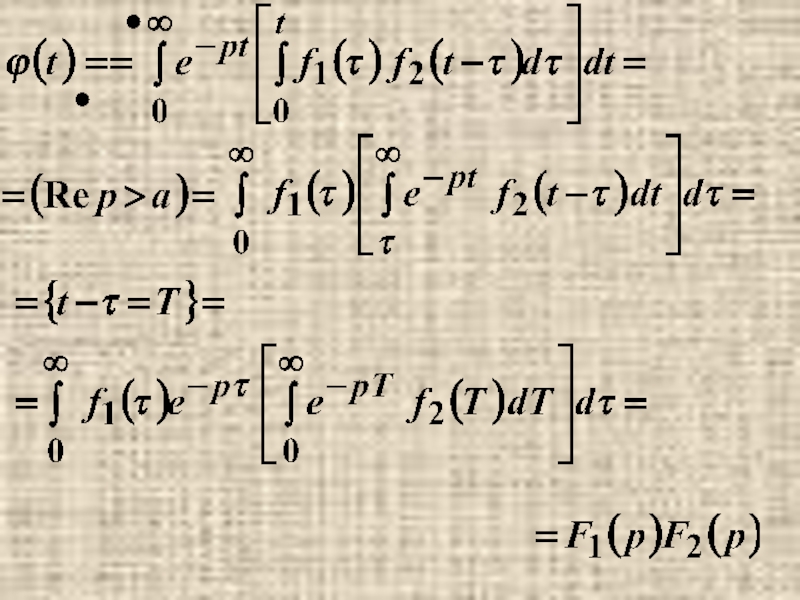

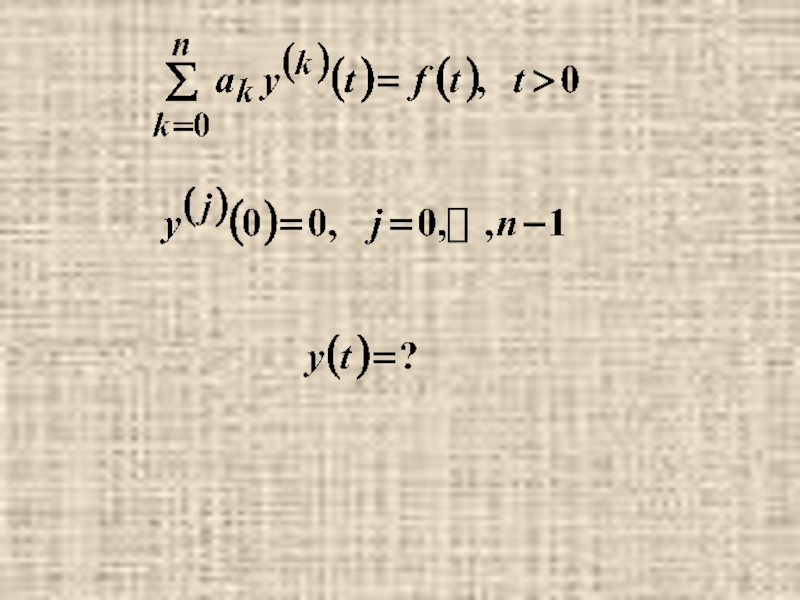
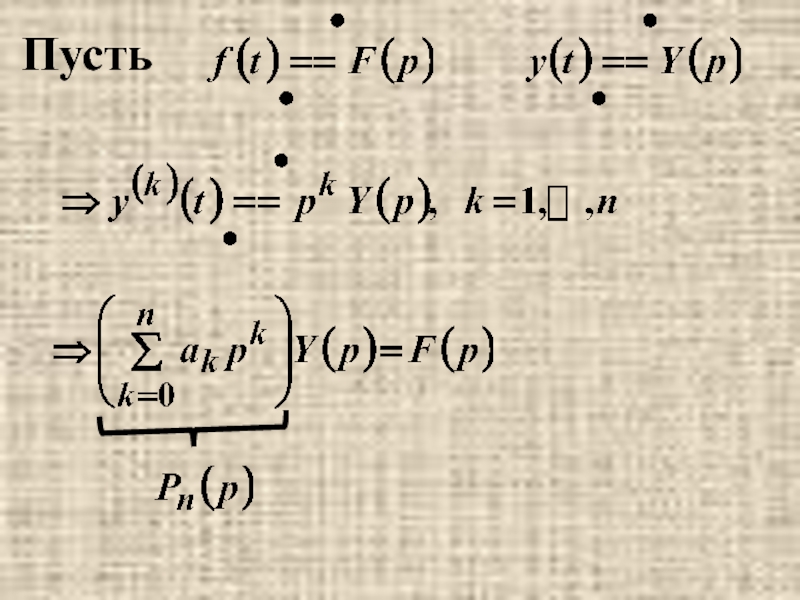
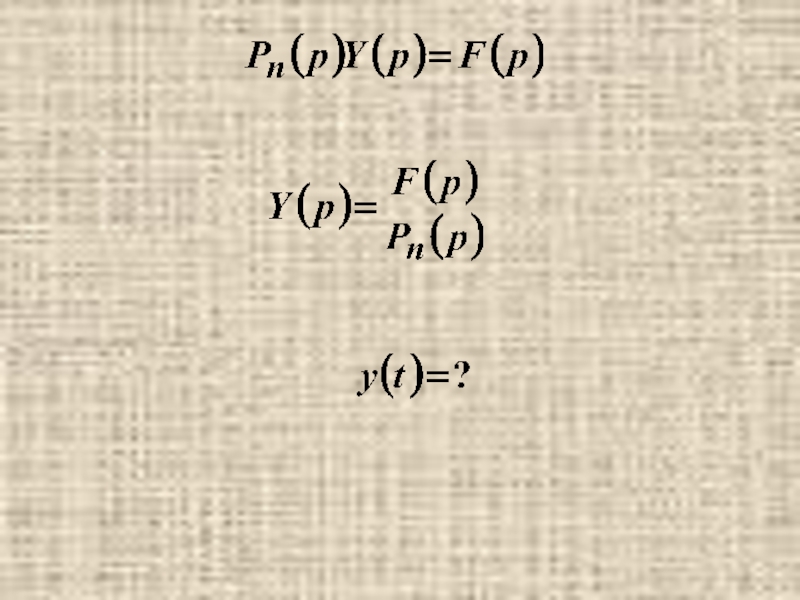
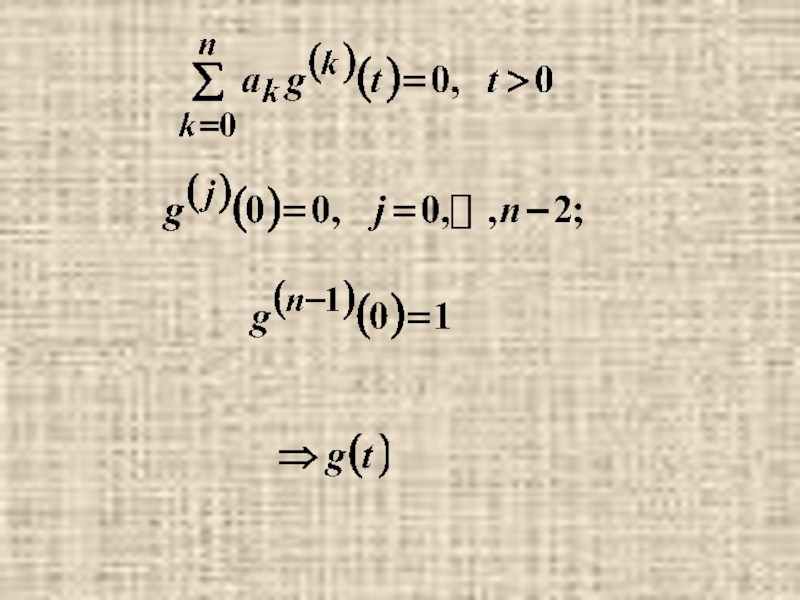
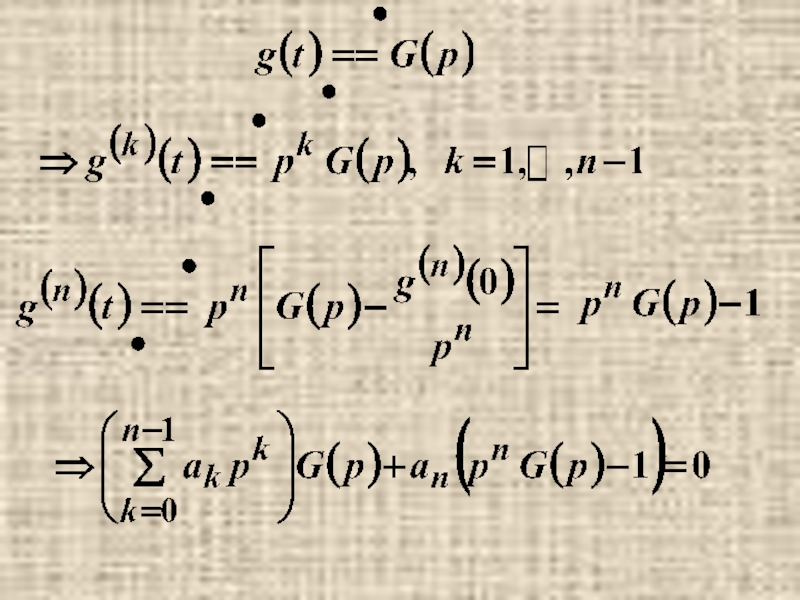
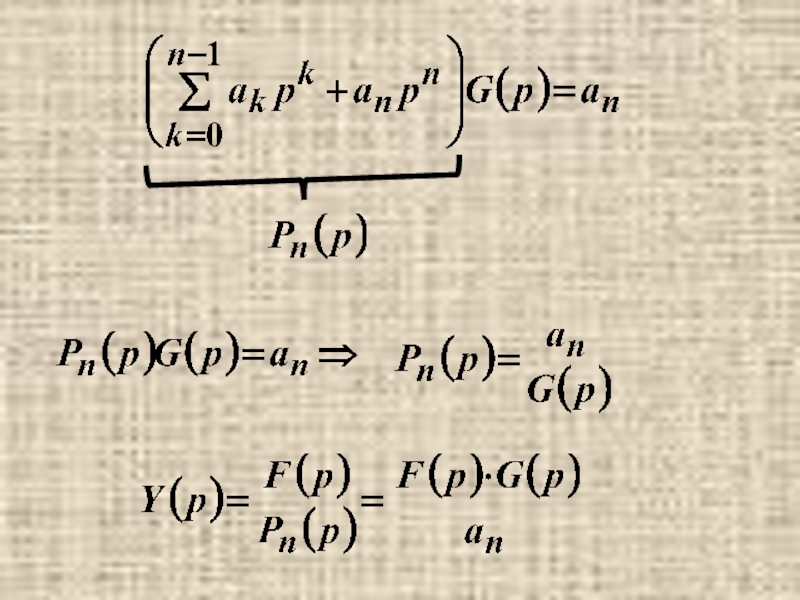
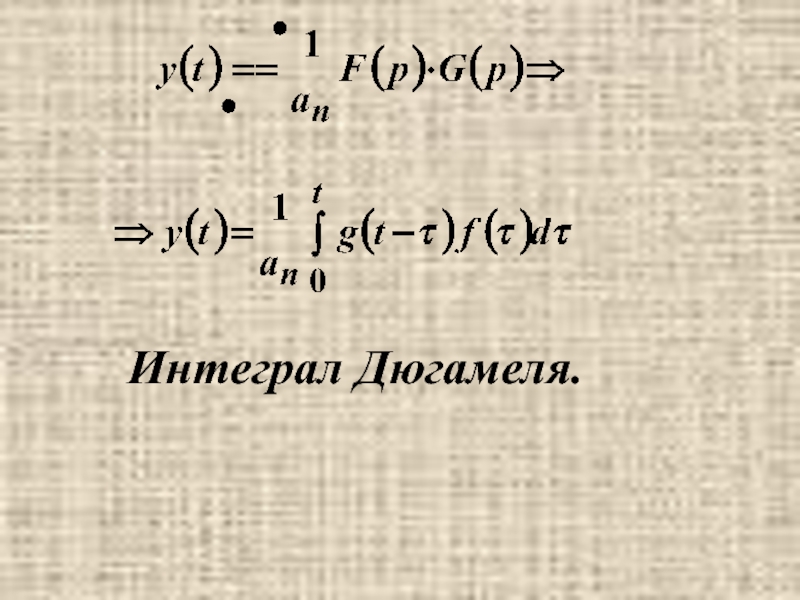

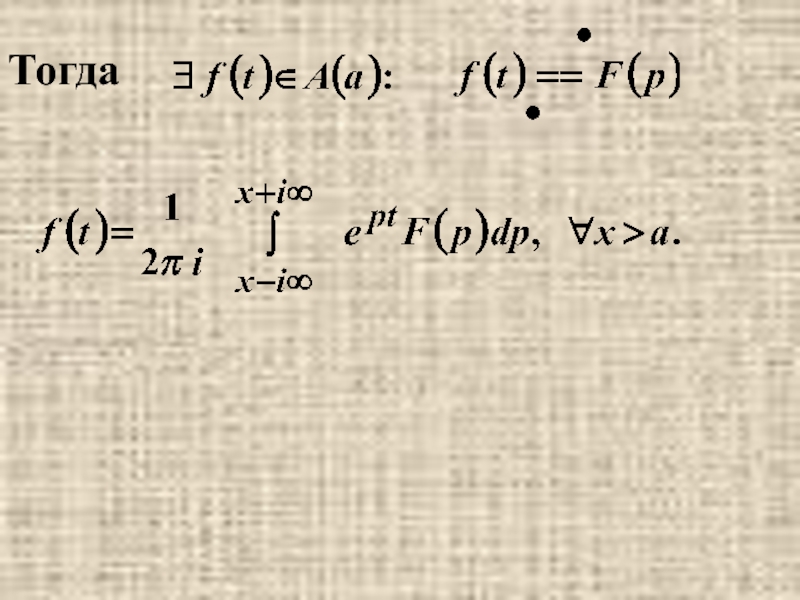

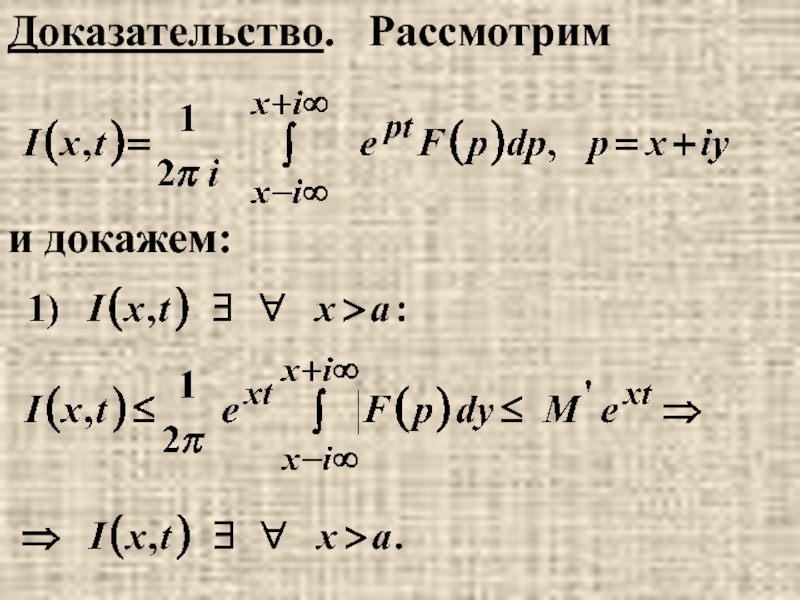
![Замечание: на ∀ [0,T] интеграл сходится равномерно по t. 2) Покажем, что I(x , t)](/img/tmb/4/340803/fec369d820e02e5639c4432ab6b52fe9-800x.jpg)