- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Случайные величины презентация
Содержание
- 1. Случайные величины
- 2. Определение Случайная величина – это переменная, которая
- 3. Дискретные и непрерывные случайные величины
- 4. Пусть Х – дискретная случайная величина с
- 5. Законом распределения случайной величины называется соотношение устанавливающее
- 6. Ряд распределения дискретной случайной величины Ряд распределения
- 7. Ряд распределения дискретной случайной величины
- 8. Графическое представление ряда распределения ДСВ называется многоугольником (полигоном) распределения
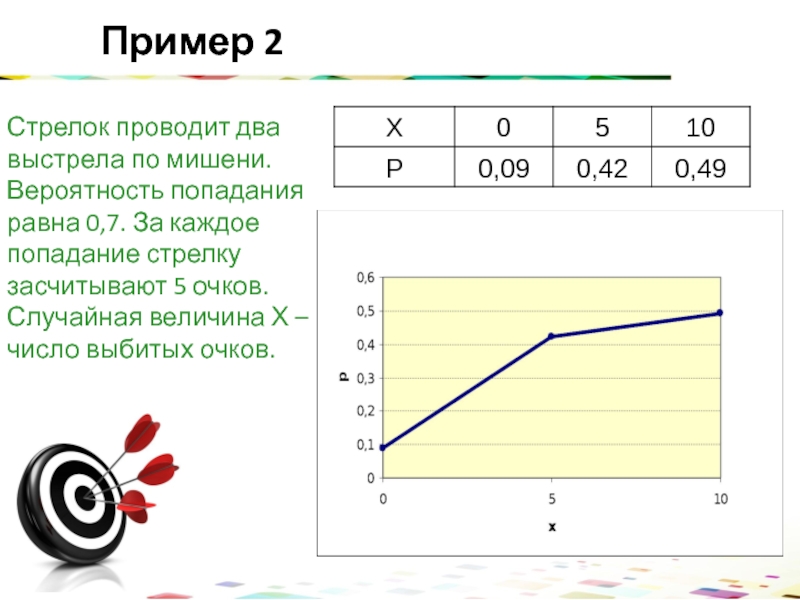
- 9. Стрелок проводит два выстрела по мишени. Вероятность
- 10. Операции над случайными величинами
- 11. Числовые характеристики дискретной случайной величины
- 12. М(С) = C, где С = const; M(C∙Х) = С∙М(Х); М(Х ± Y)
- 13. Дисперсией случайной величины называется математическое ожидание квадрата ее
- 14. D(C) = 0, где С = const; D(C∙X) = C2∙D(X);
- 15. ФОРМУЛА БЕРНУЛЛИ (биномиальный закон распределения)
- 16. ТЕОРЕМА ПУАССОНА
- 17. Функция распределения
- 18. Таким образом, значение функции распределения в точке
- 19. График функции распределения в общем случае представляет
- 20. Свойства функции распределения Функция распределения может
- 21. Решение: Пусть х ≤ 1, тогда F(x) = 0, (так как событие Х
Слайд 2Определение
Случайная величина – это переменная, которая в результате эксперимента принимает одно
Случайные величины обозначается заглавными буквами латинского алфавита, соответствующие числовые значения - строчными
Слайд 4Пусть Х – дискретная случайная величина с возможными значениями
х1, х2, …
Каждое из этих значений возможно, но не достоверно, и Х может принять любое из них с некоторой вероятностью.
Принятие случайной величиной некоторого числового значения из набора возможных (т.е. выполнение равенства X = x) есть случайное событие, характеризующееся вероятностью P(X=xi) = pi
Определение
Слайд 5Законом распределения случайной величины называется соотношение устанавливающее связь между возможными значениями
Закон распределения дискретной случайной величины может быть задан в виде:
таблицы
аналитически (в виде формулы)
графически
Закон распределения
случайных величин
Слайд 6Ряд распределения дискретной случайной величины
Ряд распределения дискретной случайной величины (ДСВ) представляет
Слайд 8Графическое представление ряда распределения ДСВ называется многоугольником (полигоном) распределения
Слайд 9Стрелок проводит два выстрела по мишени. Вероятность попадания равна 0,7. За
Пример 2
Слайд 12М(С) = C, где С = const;
M(C∙Х) = С∙М(Х);
М(Х ± Y) = М(Х) ± М(Y), где X и Y – любые случайные
М(Х∙Y)=М(Х)∙М(Y), где X и Y – независимые случайные величины;
М(Х ± C) = М(Х) ± C, где С = const.
Свойства
математического ожидания
Слайд 13Дисперсией случайной величины называется математическое ожидание квадрата ее отклонения от математического ожидания
D(X)
характеризует разброс (рассеяние) значений СВ около ее математического ожидания
Дисперсия
случайной величины
Слайд 14D(C) = 0, где С = const;
D(C∙X) = C2∙D(X);
D(X1±Х2±…±Хn) = D(X1) + D(Х2) + D(Xn),
D(X) = M(X2) – [M(X)]2
Свойства дисперсии
случайной величины
Слайд 18 Таким образом, значение функции распределения в точке х есть вероятность того,
Функция распределения определена на всей вещественной оси.
Функция распределения – самая универсальная характеристика случайной величины. Она определена как для дискретных так и для непрерывных случайных величин.
Функция распределения полностью характеризует случайную величину с вероятностной точки зрения.
Слайд 19График функции распределения в общем случае представляет собой график неубывающей функции,
Функция распределения
Слайд 20Свойства функции распределения
Функция распределения может принимать любое значение от 0
Функция распределения является не убывающей
при х2 > x1 F(x2) ≥F(x1);
lim F(x) = 0 при x → -∞ ↔ F(-∞ ) = 0 ;
lim F(x) = 1 при x → +∞ ↔ F(+∞ ) = 1 .
Вероятность попадания ДСВ в интервал [a;b) равна приращению функции распределения на этот интервал: F(a≤ x
Слайд 21Решение:
Пусть х ≤ 1, тогда F(x) = 0,
(так как событие Х
Если 2<х≤3, то F(x)=p1+p2= 0,5. Если х>3, то F(x) = p1+p2 +p3=1.
Дан ряд распределения случайной величины:
Найти и изобразить графически ее функцию распределения.
Пример 3
График функции F(х):











![Дисперсией случайной величины называется математическое ожидание квадрата ее отклонения от математического ожиданияD(X) = M[X – M(X)]2характеризует](/img/tmb/4/340459/06b37f6e712d05905ee20d1ece4dcd12-800x.jpg)













