- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Теория Автоматов презентация
Содержание
- 1. Теория Автоматов
- 2. Функциональная полнота образована соответствии с определением 1.2,
- 3. Функциональная полнота Важными для практики и интересными
- 4. Функциональная полнота Определение 1.5. Замыканием множества М
- 5. Функциональная полнота Доказательство теоремы просто. Утверждения а),
- 6. Функциональная полнота Рассмотрим конъюнктивный базис. Он является
- 7. Функциональная полнота
- 8. Функциональная полнота Пример 1.8
- 9. Алгебра Жегалкина и линейные функции Алгебра Жегалкина
- 10. Алгебра Жегалкина и линейные функции Пример 1.9
- 11. Алгебра Жегалкина и линейные функции Теорема 1.5.
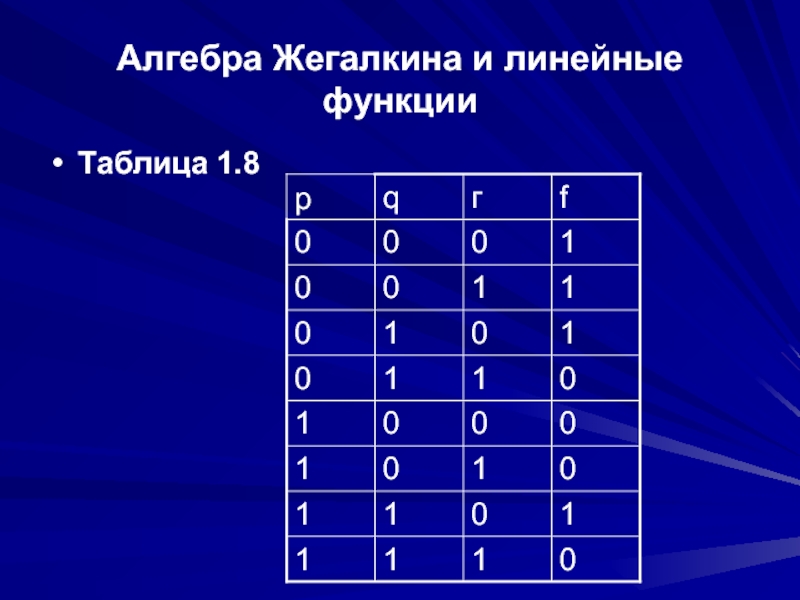
- 12. Алгебра Жегалкина и линейные функции Таблица 1.8
- 13. Алгебра Жегалкина и линейные функции Будем искать
- 14. Алгебра Жегалкина и линейные функции Г(1,1,0) =
Слайд 2Функциональная полнота
образована соответствии с определением 1.2, функционально полным набором (или базисом)
называется такое множество булевых функций, суперпозицией которых могут быть выражены любые булевы функции. Один из таких базисов — базис Буля — нами определен: это три функции И, ИЛИ, НЕ. Исследование проблем, связанных с базисами, чрезвычайно важно для практики: функции базиса — это тот полный набор строительных блоков, из которых можно строить все другие двоичные функции от любого числа переменных, а следовательно, реализовывать любые конечные функциональные прели.
Слайд 3Функциональная полнота
Важными для практики и интересными с теоретической точки зрения являются
вопросы:
Q
почему функции И, ИЛИ, НЕ такие особенные, что с их помощью можно по-
строить любую другую булеву функцию?
Q существуют ли еще какие-нибудь базисы, кроме базиса Буля? Q является ли некоторый заданный базис минимальным (то есть не содержит ли
он излишних функций, выражающихся суперпозицией других)?
Q как проверить, является ли заданный набор функций базисом, и если не является, как дополнить его другими функциями, чтобы получившееся множество составило базис?
Введем некоторые определения и обозначения
строить любую другую булеву функцию?
Q существуют ли еще какие-нибудь базисы, кроме базиса Буля? Q является ли некоторый заданный базис минимальным (то есть не содержит ли
он излишних функций, выражающихся суперпозицией других)?
Q как проверить, является ли заданный набор функций базисом, и если не является, как дополнить его другими функциями, чтобы получившееся множество составило базис?
Введем некоторые определения и обозначения
Слайд 4Функциональная полнота
Определение 1.5. Замыканием множества М булевых функций назовем такое множество
булевых функций, которые можно получить суперпозицией функций из М. Замыкание множества М обозначим [М].
Пусть В — множество всех двоичных функций. Очевидно, что множество М двоичных функций будет базисом, только если [М] = В. Рассмотрим свойства замыканий двоичных функций.
Теорема 1.4. Пусть М, N с В. Тогда:
а) Мс[М];
б) [[М]] = [М]; [В]=В;
в) McN=>[M]c[Nj
г) [М]СВ;
д) если М — базис и М с [N], то N — тоже базис
Пусть В — множество всех двоичных функций. Очевидно, что множество М двоичных функций будет базисом, только если [М] = В. Рассмотрим свойства замыканий двоичных функций.
Теорема 1.4. Пусть М, N с В. Тогда:
а) Мс[М];
б) [[М]] = [М]; [В]=В;
в) McN=>[M]c[Nj
г) [М]СВ;
д) если М — базис и М с [N], то N — тоже базис
Слайд 5Функциональная полнота
Доказательство теоремы просто. Утверждения а), б), в) и г) следуют
непосредственно из определений. Докажем д). М с [N] => [М] с [[N]~] на основании в), следовательно, [М] с [N] на основании б). Но поскольку М — базис, [М] = В. Отсюда В с [N] , но поскольку г) [N] с В, то [N] = В.
Попробуем найти другие базисы, отличные от базиса Буля. Согласно законам де Моргана, -i(p v q) = -ф-iq. Следовательно, р v q = -i(-ip-iq). Таким образом, дизъюнкция выражается через конъюнкцию и отрицание, следовательно, суперпозицией функций {И, НЕ} можно построить все функции базиса Буля — то есть ИЛИ можно выбросить из этого базиса. Некоторые другие базисы представлены в табл. 1.7. Их обоснование очевидно.
Попробуем найти другие базисы, отличные от базиса Буля. Согласно законам де Моргана, -i(p v q) = -ф-iq. Следовательно, р v q = -i(-ip-iq). Таким образом, дизъюнкция выражается через конъюнкцию и отрицание, следовательно, суперпозицией функций {И, НЕ} можно построить все функции базиса Буля — то есть ИЛИ можно выбросить из этого базиса. Некоторые другие базисы представлены в табл. 1.7. Их обоснование очевидно.
Слайд 6Функциональная полнота
Рассмотрим конъюнктивный базис. Он является минимальным, поскольку выбрасывание из множества
{И, НЕ} любой функции превращает оставшееся одноэлементное множество в не-базис. Действительно, например, с помощью суперпозиции произвольного числа функций НЕ можно построить только функцию НЕ и тождественную функцию ИДЕНТ, то есть f (х) = х. Заметим, что суперпозицией унарных функций множества М в {ИДЕНТ, НЕ} можно построить только функции этого множества. Множество булевых функций, обладающее этим свойством, называется замкнутым классом двоичных функций.
Слайд 8Функциональная полнота
Пример 1.8
Конъюнкции, то есть все функции вида х, л х2 л . . . л хт, тоже составляют замкнутый класс. Очевидно, однако, что, например, функцию, которая на наборе (0, 0, . . . , 0) имеет значение 1, нельзя представить суперпозицией таких функций. Таким образом, {И} не является базисом, следовательно, конъюнктивный базис {И, НЕ} является минимальным.
Рассмотрим более подробно базис Жегалкина.
Слайд 9Алгебра Жегалкина и линейные функции
Алгебра Жегалкина — это алгебра над множеством
двух бинарных булевых функций (И, ©) и нульарной функции 1. Легко проверить следующие соотношения в этой алгебре:
Справедливы в этой алгебре, конечно, и все соотношения табл. 1.4, включающие эти функции. Если в произвольной формуле, включающей только функции базиса Жегалкина, раскрыть скобки, то получим бесскобочную формулу, имеющую вид суммы (по модулю два) произведений, то есть некоторый полином. Он называется полиномом Жегалкина
Справедливы в этой алгебре, конечно, и все соотношения табл. 1.4, включающие эти функции. Если в произвольной формуле, включающей только функции базиса Жегалкина, раскрыть скобки, то получим бесскобочную формулу, имеющую вид суммы (по модулю два) произведений, то есть некоторый полином. Он называется полиномом Жегалкина
Слайд 11Алгебра Жегалкина и линейные функции
Теорема 1.5. Любая булева функция может быть
представлена в виде полинома Жегалкина, причем единственным образом.
Доказательство. Существование полинома для любой функции гарантируется тем, что функции {И, 0,1} образуют базис. Далее, легко видеть, что число возможных членов в полиноме с m переменными равно 2т. Поэтому число различных полиномов Жегалкина от m переменных равно 2 в степени 2т, то есть числу возможных двоичных функций от m переменных. Поскольку одна и та же формула не может представлять различные функции, то тем самым между множествами двоичных функций и полиномов Жегалкина от m переменных установлено взаимнооднозначное соотношение.
Пример 1.10
Построим для функции f (p, q, r) = -ip vq0rq(pvr) примера 1.2 полиномом Жегалкина непосредственно из таблицы истинности (см. табл. 1.3). Эту таблицу повторим здесь.
Доказательство. Существование полинома для любой функции гарантируется тем, что функции {И, 0,1} образуют базис. Далее, легко видеть, что число возможных членов в полиноме с m переменными равно 2т. Поэтому число различных полиномов Жегалкина от m переменных равно 2 в степени 2т, то есть числу возможных двоичных функций от m переменных. Поскольку одна и та же формула не может представлять различные функции, то тем самым между множествами двоичных функций и полиномов Жегалкина от m переменных установлено взаимнооднозначное соотношение.
Пример 1.10
Построим для функции f (p, q, r) = -ip vq0rq(pvr) примера 1.2 полиномом Жегалкина непосредственно из таблицы истинности (см. табл. 1.3). Эту таблицу повторим здесь.
Слайд 13Алгебра Жегалкина и линейные функции
Будем искать коэффициенты полинома
, : .
f (p, q, r) = a0 0appeaqq0arreapqpqe aprpr0 aqrqr0 a^pqr . , ,.f
Всего коэффициентов 8, каждый коэффициент может быть 0 или 1, число возможных вариантов равно 28 =* 256 — как раз столько, сколько всех возможных булевых функций от трех переменных. Для нахождения коэффициентов заданной функции используем таблицу ее значений.
Искомые коэффициенты последовательно найдем из следующей системы уравнений:
f (0,0,0) = 1 = a0; отсюда а0 = 1;
f (1,0,0) = 0 = а0Фар = 10ap; отсюда ар =1;
Г(0,1,0) = 1 = а00ач=10ач;отсюдаач==0;
f (0,0,1) = 1 = a0 ©ar = 10ar; отсюда ar = 0;
f (p, q, r) = a0 0appeaqq0arreapqpqe aprpr0 aqrqr0 a^pqr . , ,.f
Всего коэффициентов 8, каждый коэффициент может быть 0 или 1, число возможных вариантов равно 28 =* 256 — как раз столько, сколько всех возможных булевых функций от трех переменных. Для нахождения коэффициентов заданной функции используем таблицу ее значений.
Искомые коэффициенты последовательно найдем из следующей системы уравнений:
f (0,0,0) = 1 = a0; отсюда а0 = 1;
f (1,0,0) = 0 = а0Фар = 10ap; отсюда ар =1;
Г(0,1,0) = 1 = а00ач=10ач;отсюдаач==0;
f (0,0,1) = 1 = a0 ©ar = 10ar; отсюда ar = 0;
Слайд 14Алгебра Жегалкина и линейные функции
Г(1,1,0) = 1 = а0Фар0ачеар(1=1е1еоеа1Х1;отсюдаарч=1;
f(l,0,l) = 0
= a0®ap0ar0apr =101000apr; отсюда apr =0;
Г(0,1,1) = 0 = а00ач0аг0ачг = 100000ачг;отсюда aqr =1Найденное представление совпадает с представлением, полученным для этой функции ранее аналитически: f (p, q, г) = 1 Ф р Ф pq 0 qr .
Булева функция, полином Жегалкина которой имеет вид а0 ©Хах1х{, называется линейной.
Г(0,1,1) = 0 = а00ач0аг0ачг = 100000ачг;отсюда aqr =1Найденное представление совпадает с представлением, полученным для этой функции ранее аналитически: f (p, q, г) = 1 Ф р Ф pq 0 qr .
Булева функция, полином Жегалкина которой имеет вид а0 ©Хах1х{, называется линейной.