- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Задачи ОГЭ и ЕГЭ по геометрии презентация
Содержание
- 1. Задачи ОГЭ и ЕГЭ по геометрии
- 2. Окружность проходит через вершины А и
- 3. Окружность проходит через вершины А и
- 4. Окружность проходит через вершины А и
- 5. Окружность проходит через вершины А и
- 6. Окружность проходит через вершины А и
- 7. Окружность проходит через вершины А и
- 8. Окружность проходит через вершины А и
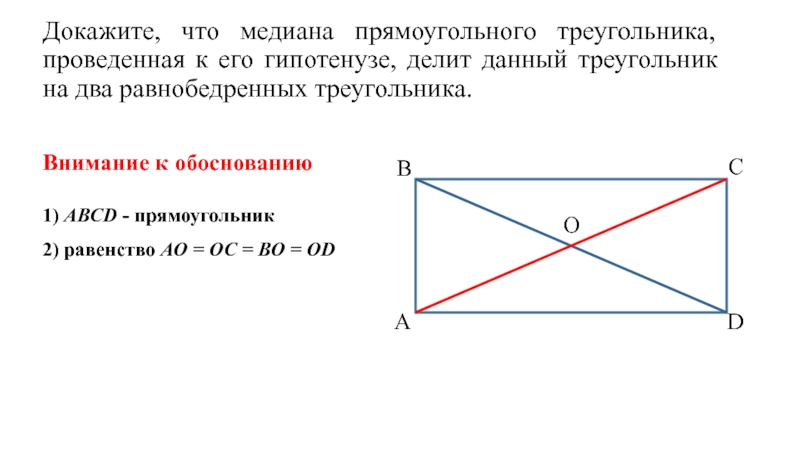
- 9. Докажите, что медиана прямоугольного треугольника, проведенная
- 10. Докажите, что медиана прямоугольного треугольника, проведенная
- 11. Докажите, что медиана прямоугольного треугольника, проведенная
- 12. Докажите, что медиана прямоугольного треугольника, проведенная
- 13. Докажите, что медиана прямоугольного треугольника, проведенная
- 14. Высоты ВВ1 и СС1 остроугольного треугольника
- 15. Высоты ВВ1 и СС1 остроугольного треугольника
- 16. Высоты ВВ1 и СС1 остроугольного треугольника
- 17. Высоты ВВ1 и СС1 остроугольного треугольника
- 18. Высоты ВВ1 и СС1 остроугольного треугольника
- 19. Высоты ВВ1 и СС1 остроугольного треугольника
- 20. ПОВТОРЕНИЕ Задачи - сюжеты Когда считать «доказано»
- 21. Задачи – сюжеты В параллелограмме стороны
- 22. Когда считать «доказано» В параллелограмме ABCD
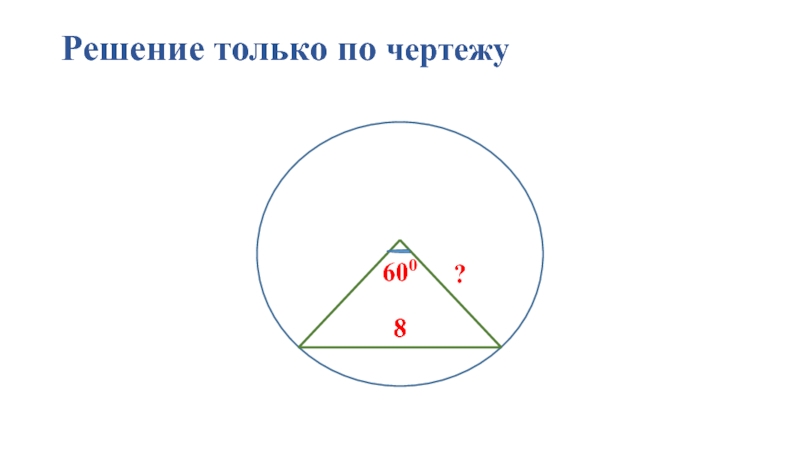
- 23. Решение только по чертежу ? 8 8 600
- 24. Разные способы в одном сюжете Найдите
Окружность проходит через вершины А и С треугольника АВС и пересекает стороны АВ и ВС в точках К и Р соответственно. Отрезки АР и КС пересекаются в точке F. Найдите
Слайд 1«Задачи ОГЭ и ЕГЭ по геометрии – организация итогового повторения и
предупреждение ошибок учащихся»
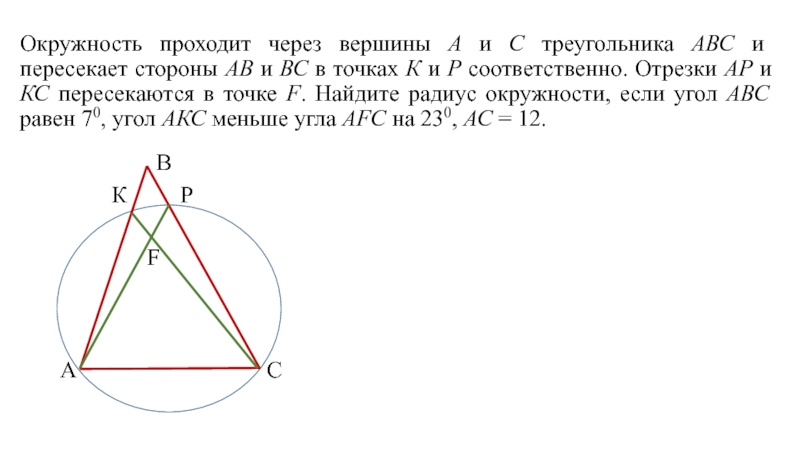
Слайд 2 Окружность проходит через вершины А и С треугольника АВС и пересекает
стороны АВ и ВС в точках К и Р соответственно. Отрезки АР и КС пересекаются в точке F. Найдите радиус окружности, если угол АВС равен 70, угол АКС меньше угла АFС на 230, АС = 12.
Задача 1 (вариант ОГЭ).
Слайд 3 Окружность проходит через вершины А и С треугольника АВС и пересекает
стороны АВ и ВС в точках К и Р соответственно. Отрезки АР и КС пересекаются в точке F. Найдите радиус окружности, если угол АВС равен 70, угол АКС меньше угла АFС на 230, АС = 12.
А
С
К
В
Р
F
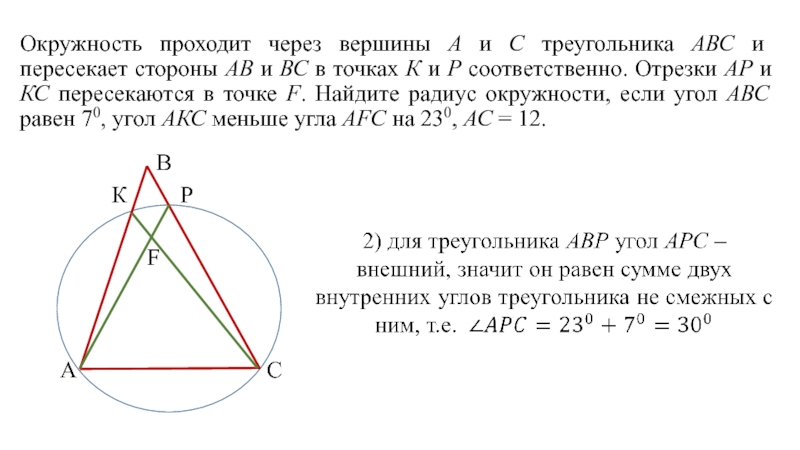
Слайд 4 Окружность проходит через вершины А и С треугольника АВС и пересекает
стороны АВ и ВС в точках К и Р соответственно. Отрезки АР и КС пересекаются в точке F. Найдите радиус окружности, если угол АВС равен 70, угол АКС меньше угла АFС на 230, АС = 12.
А
С
К
В
Р
F
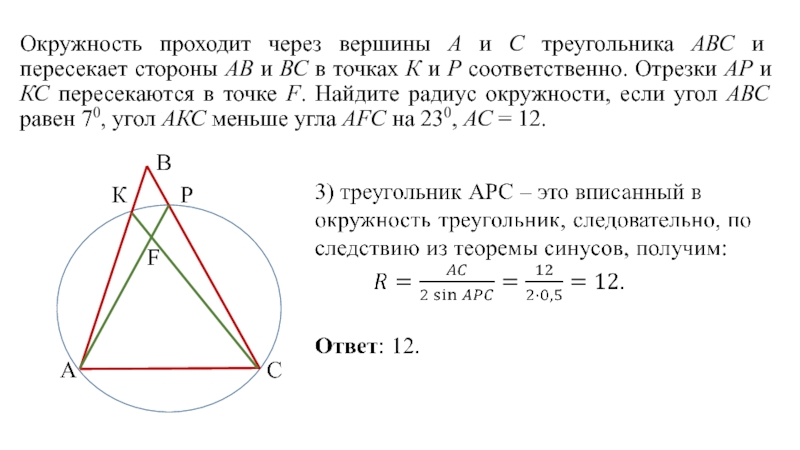
Слайд 5 Окружность проходит через вершины А и С треугольника АВС и пересекает
стороны АВ и ВС в точках К и Р соответственно. Отрезки АР и КС пересекаются в точке F. Найдите радиус окружности, если угол АВС равен 70, угол АКС меньше угла АFС на 230, АС = 12.
А
С
К
В
Р
F
Слайд 6 Окружность проходит через вершины А и С треугольника АВС и пересекает
стороны АВ и ВС в точках К и Р соответственно. Отрезки АР и КС пересекаются в точке F. Найдите радиус окружности, если угол АВС равен 70, угол АКС меньше угла АFС на 230, АС = 12.
А
С
К
В
Р
F
Слайд 7 Окружность проходит через вершины А и С треугольника АВС и пересекает
стороны АВ и ВС в точках К и Р соответственно. Отрезки АР и КС пересекаются в точке F. Найдите радиус окружности, если угол АВС равен 70, угол АКС меньше угла АFС на 230, АС = 12.
А
С
К
В
Р
F
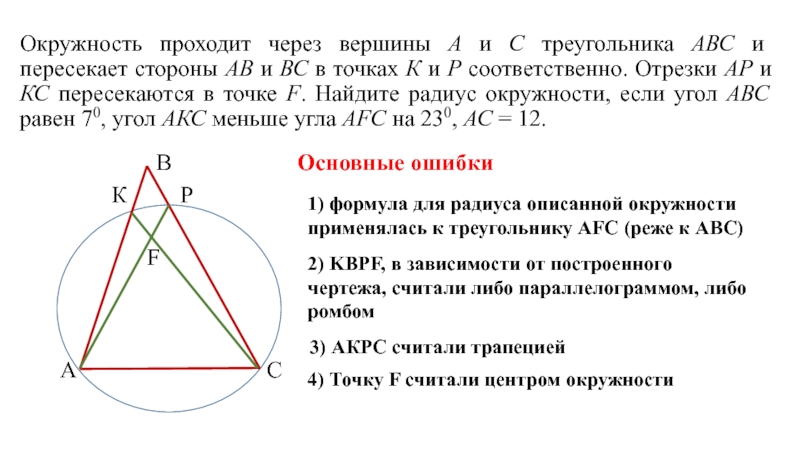
Основные ошибки
1) формула для радиуса описанной окружности применялась к треугольнику AFC (реже к АВС)
2) KBPF, в зависимости от построенного чертежа, считали либо параллелограммом, либо ромбом
4) Точку F считали центром окружности
3) АКРC считали трапецией
Слайд 8 Окружность проходит через вершины А и С треугольника АВС и пересекает
стороны АВ и ВС в точках К и Р соответственно. Отрезки АР и КС пересекаются в точке F. Найдите радиус окружности, если угол АВС равен 70, угол АКС меньше угла АFС на 230, АС = 12.
А
С
К
В
Р
F
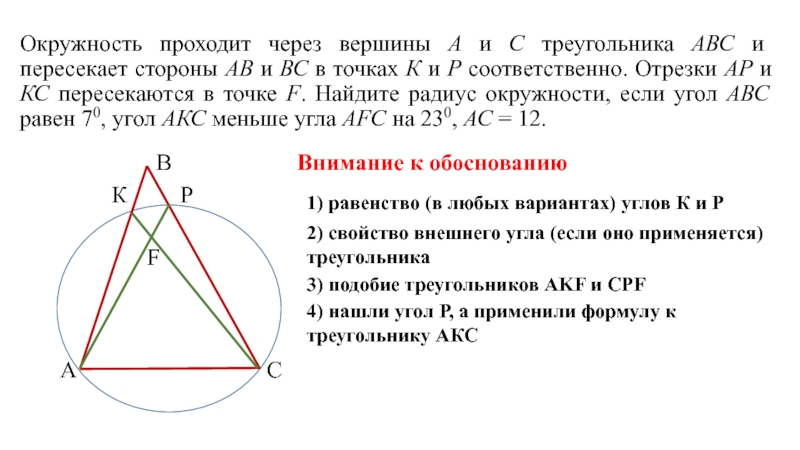
Внимание к обоснованию
1) равенство (в любых вариантах) углов К и Р
2) свойство внешнего угла (если оно применяется) треугольника
3) подобие треугольников AKF и CPF
4) нашли угол Р, а применили формулу к треугольнику АКС
Слайд 9 Докажите, что медиана прямоугольного треугольника, проведенная к его гипотенузе, делит данный
треугольник на два равнобедренных треугольника.
Задача 2 (вариант ОГЭ).
Слайд 10 Докажите, что медиана прямоугольного треугольника, проведенная к его гипотенузе, делит данный
треугольник на два равнобедренных треугольника.
С
С
А
В
О
А
В
D
О
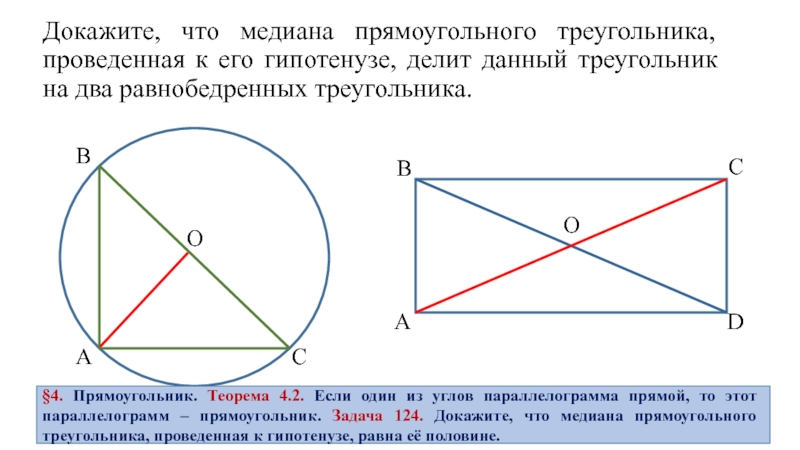
§4. Прямоугольник. Теорема 4.2. Если один из углов параллелограмма прямой, то этот параллелограмм – прямоугольник. Задача 124. Докажите, что медиана прямоугольного треугольника, проведенная к гипотенузе, равна её половине.
Слайд 11 Докажите, что медиана прямоугольного треугольника, проведенная к его гипотенузе, делит данный
треугольник на два равнобедренных треугольника.
С
А
В
О
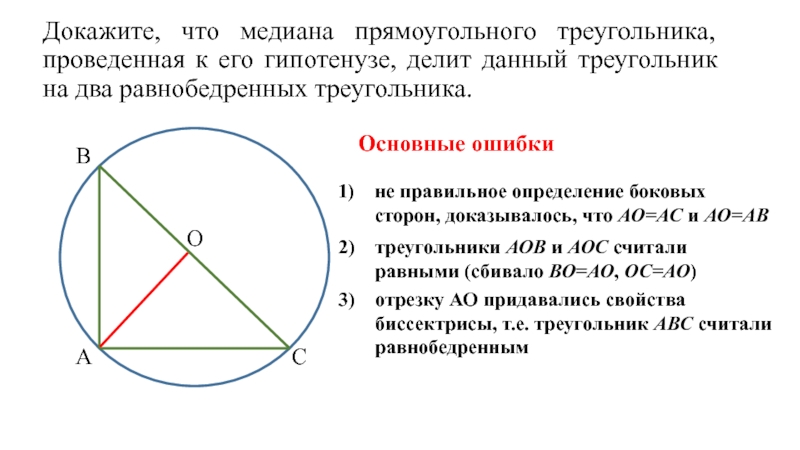
Основные ошибки
не правильное определение боковых сторон, доказывалось, что АО=АС и АО=АВ
треугольники АОВ и АОС считали
равными (сбивало ВО=АО, ОС=АО)
отрезку АО придавались свойства
биссектрисы, т.е. треугольник АВС считали
равнобедренным
Слайд 12 Докажите, что медиана прямоугольного треугольника, проведенная к его гипотенузе, делит данный
треугольник на два равнобедренных треугольника.
С
А
В
О
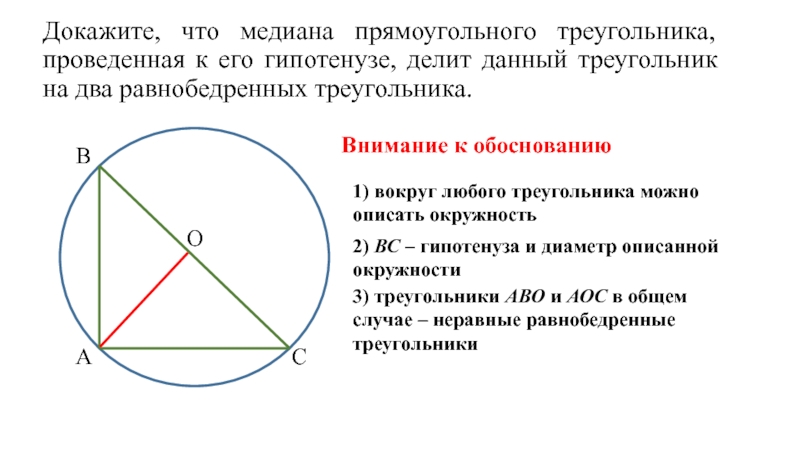
Внимание к обоснованию
1) вокруг любого треугольника можно описать окружность
2) ВС – гипотенуза и диаметр описанной окружности
3) треугольники АВО и АОС в общем случае – неравные равнобедренные треугольники
Слайд 13 Докажите, что медиана прямоугольного треугольника, проведенная к его гипотенузе, делит данный
треугольник на два равнобедренных треугольника.
С
А
В
D
О
Внимание к обоснованию
1) АВСD - прямоугольник
2) равенство АО = ОС = ВО = ОD
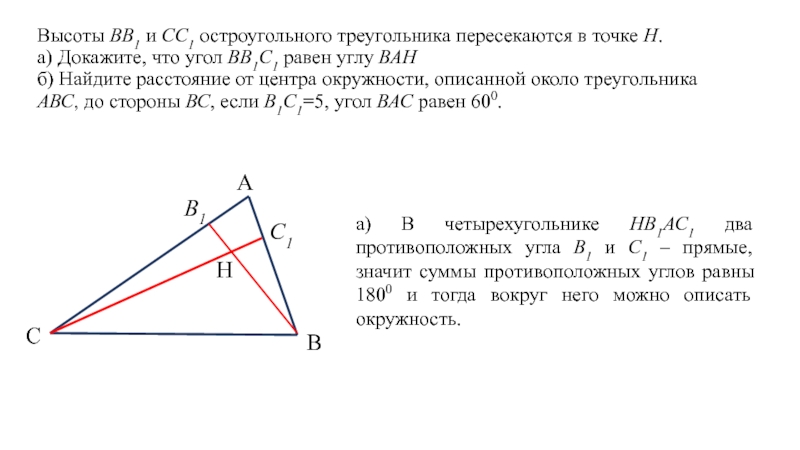
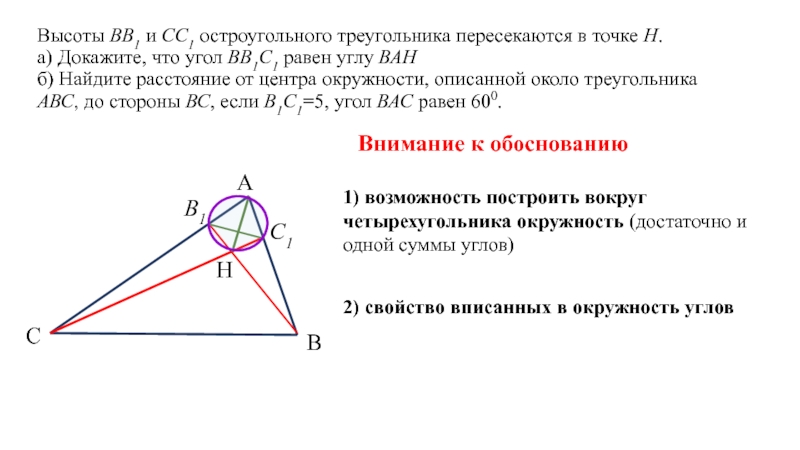
Слайд 14 Высоты ВВ1 и СС1 остроугольного треугольника пересекаются в точке Н. а) Докажите,
что угол ВВ1С1 равен углу ВАН
б) Найдите расстояние от центра окружности, описанной около треугольника АВС, до стороны ВС, если В1С1=5, угол ВАС равен 600.
Задача 3 (вариант ЕГЭ).
Слайд 15 Высоты ВВ1 и СС1 остроугольного треугольника пересекаются в точке Н. а) Докажите,
что угол ВВ1С1 равен углу ВАН
б) Найдите расстояние от центра окружности, описанной около треугольника АВС, до стороны ВС, если В1С1=5, угол ВАС равен 600.
А
В
С
С1
В1
Н
а) В четырехугольнике НВ1АС1 два противоположных угла В1 и С1 – прямые, значит суммы противоположных углов равны 1800 и тогда вокруг него можно описать окружность.
Слайд 16 Высоты ВВ1 и СС1 остроугольного треугольника пересекаются в точке Н. а) Докажите,
что угол ВВ1С1 равен углу ВАН
б) Найдите расстояние от центра окружности, описанной около треугольника АВС, до стороны ВС, если В1С1=5, угол ВАС равен 600.
А
В
С
С1
В1
Н
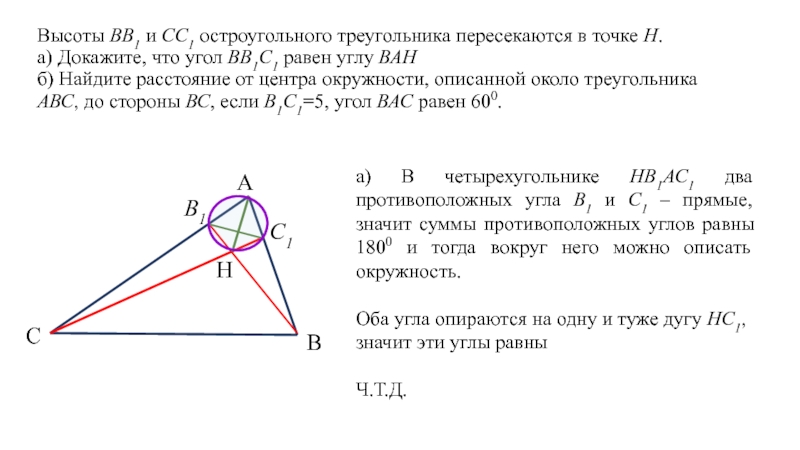
а) В четырехугольнике НВ1АС1 два противоположных угла В1 и С1 – прямые, значит суммы противоположных углов равны 1800 и тогда вокруг него можно описать окружность.
Оба угла опираются на одну и туже дугу НС1, значит эти углы равны
Ч.Т.Д.
Слайд 17 Высоты ВВ1 и СС1 остроугольного треугольника пересекаются в точке Н. а) Докажите,
что угол ВВ1С1 равен углу ВАН
б) Найдите расстояние от центра окружности, описанной около треугольника АВС, до стороны ВС, если В1С1=5, угол ВАС равен 600.
А
В
С
С1
В1
Н
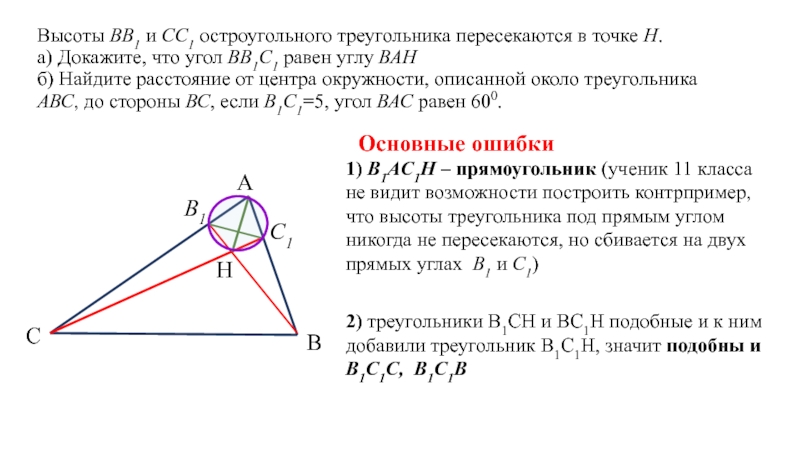
Основные ошибки
1) В1АС1Н – прямоугольник (ученик 11 класса не видит возможности построить контрпример, что высоты треугольника под прямым углом никогда не пересекаются, но сбивается на двух прямых углах В1 и С1)
2) треугольники В1СН и ВС1Н подобные и к ним добавили треугольник В1С1Н, значит подобны и В1С1С, В1С1В
Слайд 18 Высоты ВВ1 и СС1 остроугольного треугольника пересекаются в точке Н. а) Докажите,
что угол ВВ1С1 равен углу ВАН
б) Найдите расстояние от центра окружности, описанной около треугольника АВС, до стороны ВС, если В1С1=5, угол ВАС равен 600.
А
В
С
С1
В1
Н
Внимание к обоснованию
1) возможность построить вокруг четырехугольника окружность (достаточно и одной суммы углов)
2) свойство вписанных в окружность углов
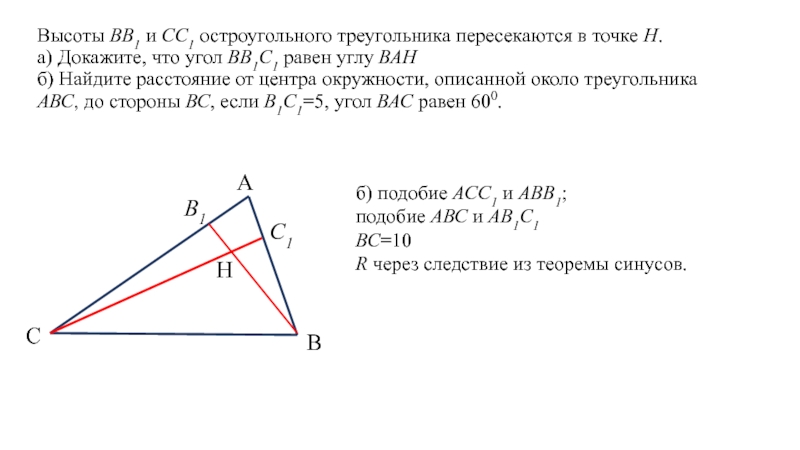
Слайд 19 Высоты ВВ1 и СС1 остроугольного треугольника пересекаются в точке Н. а) Докажите,
что угол ВВ1С1 равен углу ВАН
б) Найдите расстояние от центра окружности, описанной около треугольника АВС, до стороны ВС, если В1С1=5, угол ВАС равен 600.
А
В
С
С1
В1
Н
б) подобие АСС1 и АВВ1;
подобие АВС и АВ1С1
ВС=10
R через следствие из теоремы синусов.
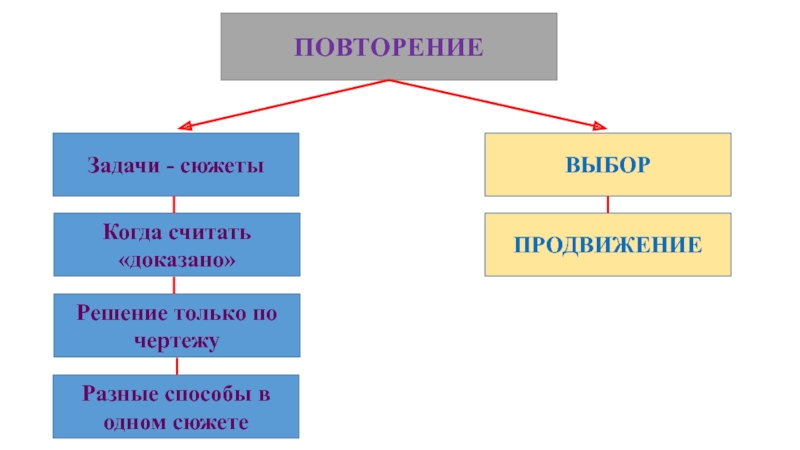
Слайд 20ПОВТОРЕНИЕ
Задачи - сюжеты
Когда считать «доказано»
Решение только по чертежу
ВЫБОР
ПРОДВИЖЕНИЕ
Разные способы в одном
сюжете
Слайд 21Задачи – сюжеты В параллелограмме стороны 6 см и 8 см
образуют угол в 600. Что можно найти?
диагонали
площадь
высоту
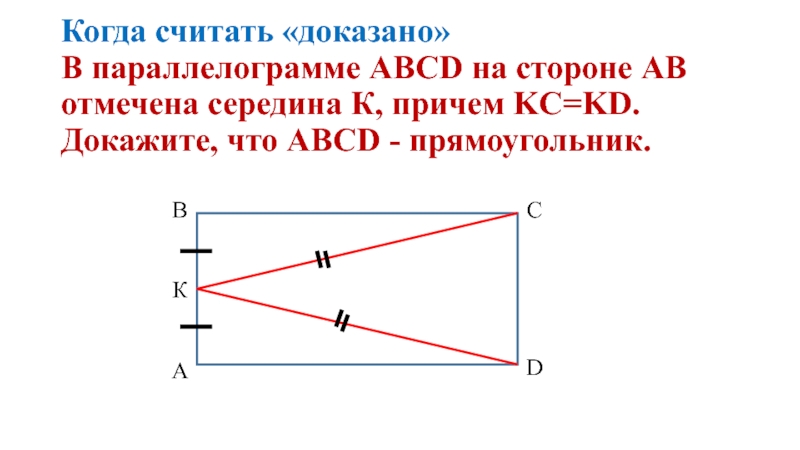
Слайд 22 Когда считать «доказано» В параллелограмме ABCD на стороне АВ отмечена середина К,
причем KC=KD. Докажите, что ABCD - прямоугольник.
С
А
К
В
D
Слайд 24Разные способы в одном сюжете Найдите площадь равностороннего треугольника со стороной
8 см.
Только «наметки»
Аукцион
Полные решения в вариантах (3-4)
