- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Производная. Правила вычисления производных презентация
Содержание
x0 Δx f(x0) x f(x) Δf y=f(x) Δx = x - x0 x = x0 + Δx приращение аргумента Δf = f(x) – f(x0) f(x) = f(x0) + Δf
Слайд 2
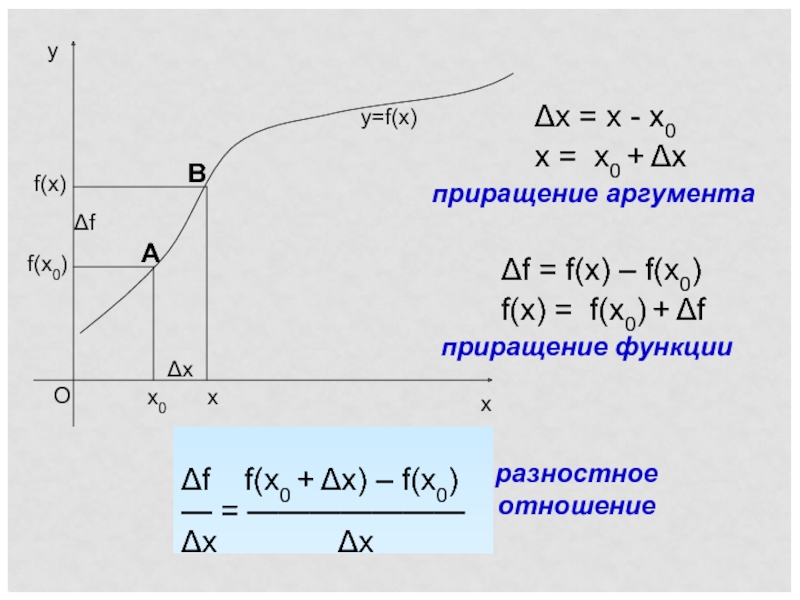
x0
Δx
f(x0)
x
f(x)
Δf
y=f(x)
Δx = x - x0
x = x0 + Δx
приращение аргумента
Δf
= f(x) – f(x0)
f(x) = f(x0) + Δf
приращение функции
Δf f(x0 + Δx) – f(x0)
— = ———————
Δx Δx
разностное отношение
А
В
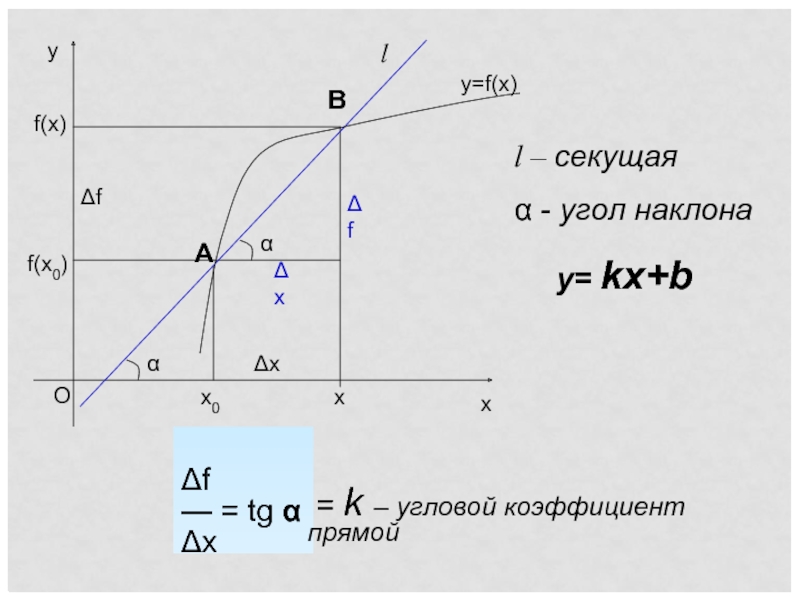
Слайд 3f(x0)
f(x)
Δx
Δf
l
l – секущая
α - угол наклона
Δf
— = tg α
Δx
= k
– угловой коэффициент прямой
y= kx+b
Слайд 4x
Если тело движется по прямой и за время Δt его координата
изменяется на Δx, то
Δt t(x0 + Δx) – t(x0)
Vср(Δt) = — = ———————
Δx Δx
- средняя скорость движения тела за Δt
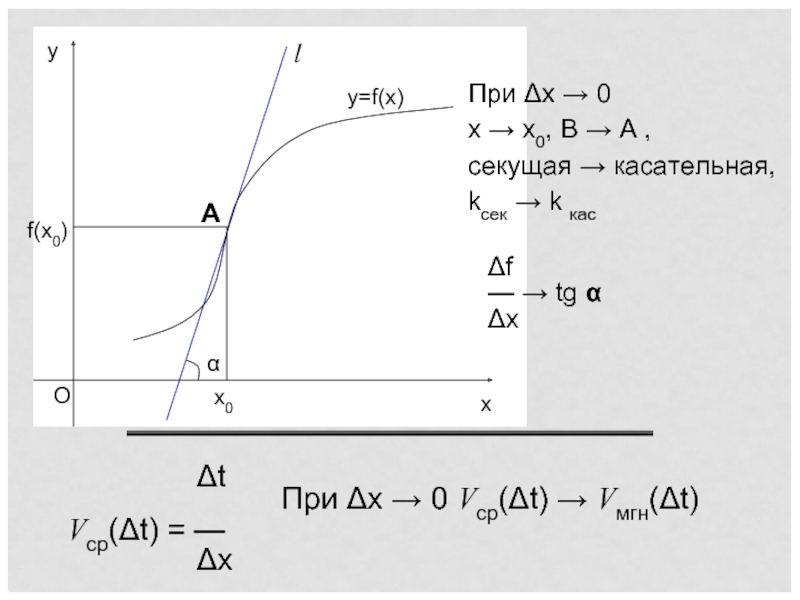
Слайд 5При Δx → 0
x → x0, B →
A ,
секущая → касательная,
kсек → k кас
секущая → касательная,
kсек → k кас
Δf
— → tg α
Δx
Δt
Vср(Δt) = —
Δx
При Δx → 0 Vср(Δt) → Vмгн(Δt)
Слайд 6Производная
Производной функции f в точке x0 называется число, к которому стремится
разностное отношение при Δx → 0.
Δf f(x0 + Δx) – f(x0)
f´(x0)= — = ———————
Δx Δx
при Δx → 0.
Слайд 7Правила вычисления производных
Если функции U и V дифференцируемы в точке x0,
то
Если функция U дифференцируема в точке x0, а С-постоянная, то (СU)´=CU´
