В. Ю.
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Метод главных элементов для решения системы линейных уравнений презентация
Содержание
- 1. Метод главных элементов для решения системы линейных уравнений
- 2. Формулы:
- 3. продолжение
- 4. продолжение
- 5. Схему вычислений по методу Гаусса с выбором главного элемента поясняет следующий пример:
- 6. Решение ведется в таблице 1.
- 7. продолжение
- 8. продолжение
- 9. продолжение
- 10. продолжение
- 11. продолжение
- 12. продолжение Практически, вследствие вычислительных погрешностей, полученное методом
- 13. продолжение где
- 14. продолжение
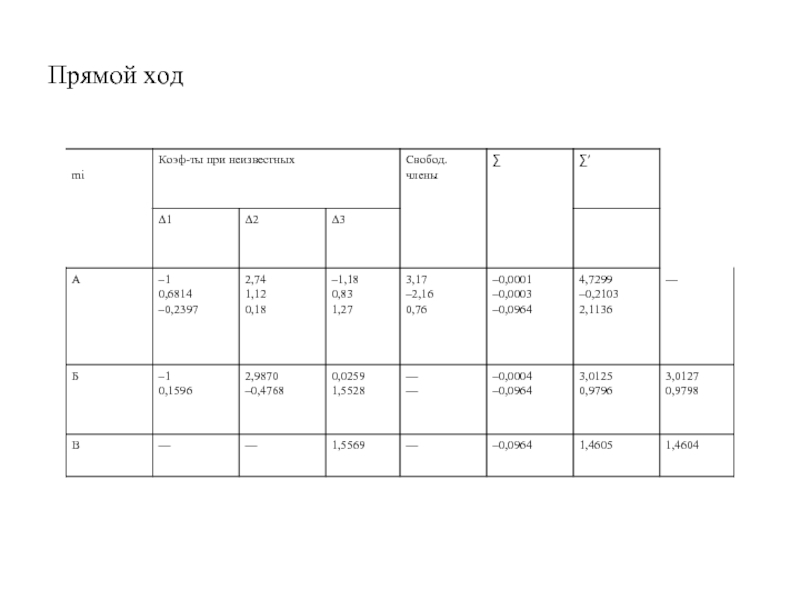
- 15. Прямой ход
- 16. Обратный ход.
- 17. Спасибо за внимание!
Слайд 1Метод главных элементов для решения системы линейных уравнений
Студент группы: ФМ-12-15
Мижеев
Слайд 12продолжение
Практически, вследствие вычислительных погрешностей, полученное методом Гаусса решение системы является приближенным.
Покажем, как уточнить это решение.
Пусть для системы получено приближенное решение Положим .
Тогда для вектора поправки будем иметь
уравнение или
Пусть для системы получено приближенное решение Положим .
Тогда для вектора поправки будем иметь
уравнение или
Слайд 13продолжение
где
– вектор невязок для приближенного решения . Таким образом, чтобы найти , нужно решить систему с прежней матрицей A и новым вектором свободных членов . Заметим, что преобразованные коэффициенты матрицы A можно не уточнять, так как при малых невязках соответствующие ошибки будут иметь более высокий порядок малости.