- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Векторы в пространстве презентация
Содержание
- 1. Векторы в пространстве
- 2. Понятие вектора Отрезок, для которого указано, какой
- 3. Нулевой вектор Любая точка пространства также может
- 4. Длина вектора Длиной ненулевого вектора
- 5. Коллинеарные векторы Два ненулевых вектора называются
- 6. Сонаправленные векторы Если два ненулевых вектора АВ
- 7. Противоположно направленные векторы Если два ненулевых вектора
- 8. Сонаправленность нулевого вектора Нулевой вектор условимся считать
- 9. Векторы в параллелепипеде Векторы AD и AM
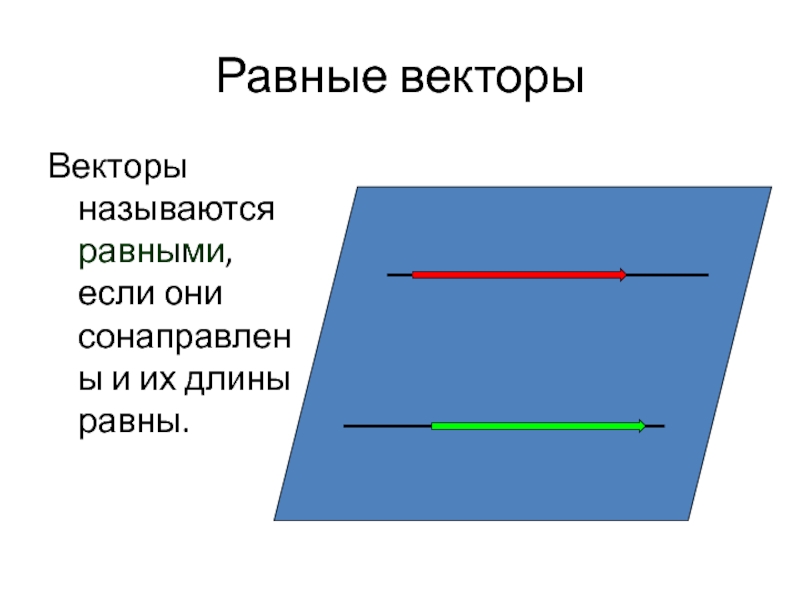
- 10. Равные векторы Векторы называются равными, если они сонаправлены и их длины равны.
- 11. Равенство векторов Если точка А - начало
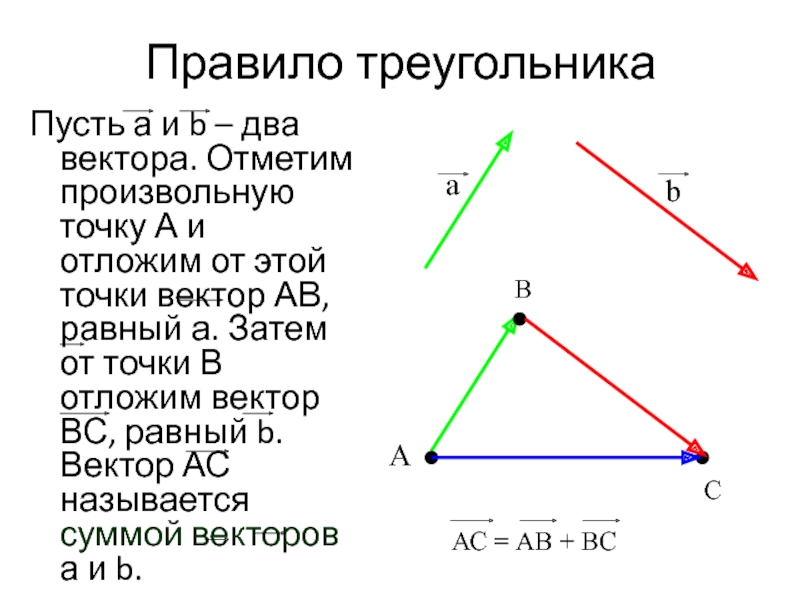
- 12. Правило треугольника Пусть а и b –
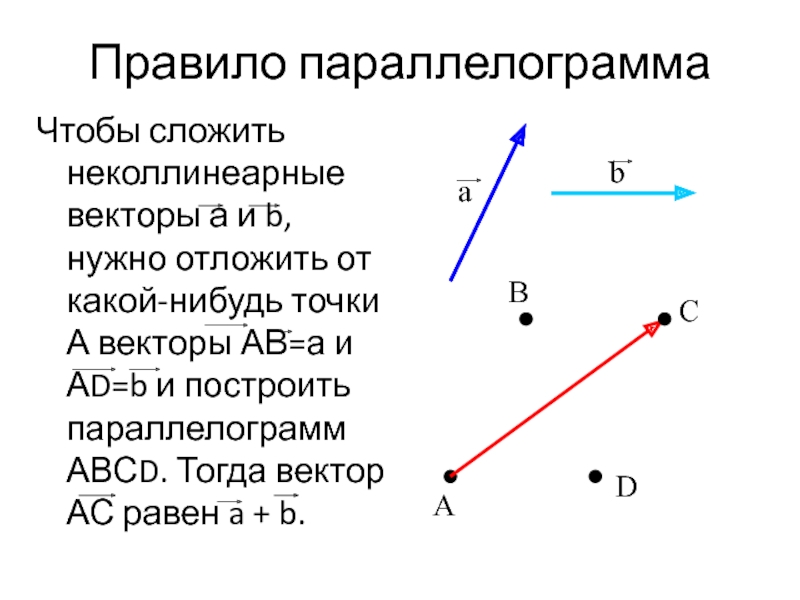
- 13. Правило параллелограмма Чтобы сложить неколлинеарные векторы а
- 14. Вычитание векторов Разностью векторов а
- 15. Вычитание векторов Теорема: Для любых векторов
- 16. Умножение вектора на число Произведением ненулевого вектора
- 17. Компланарные векторы Векторы называются компланарными, если при
- 18. Компланарные векторы Любые два вектора компланарны. Три
- 19. Признак компланарности трёх векторов Если вектор с
- 20. Обратное утверждение Если векторы а, b и
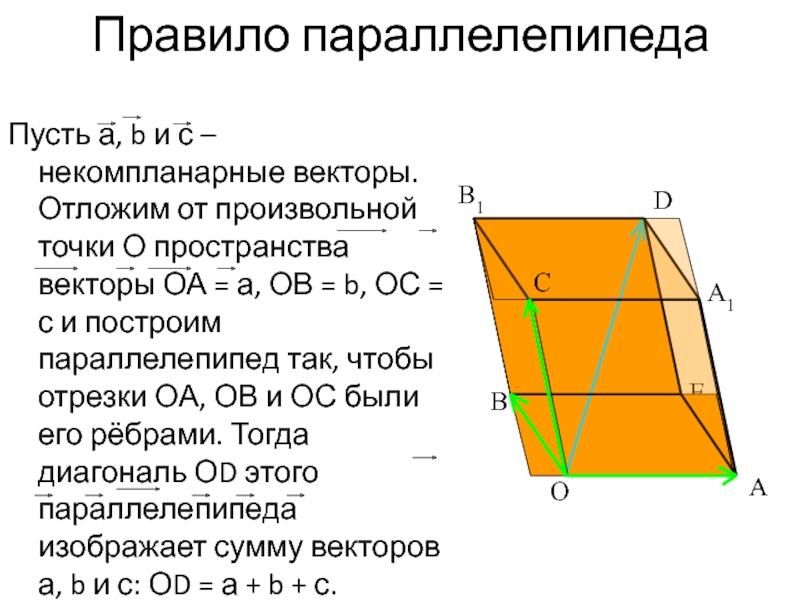
- 21. Правило параллелепипеда Пусть а, b и с
- 22. Разложение вектора по двум некомпланарным векторам Если
- 23. Теорема Любой вектор можно разложить по трём
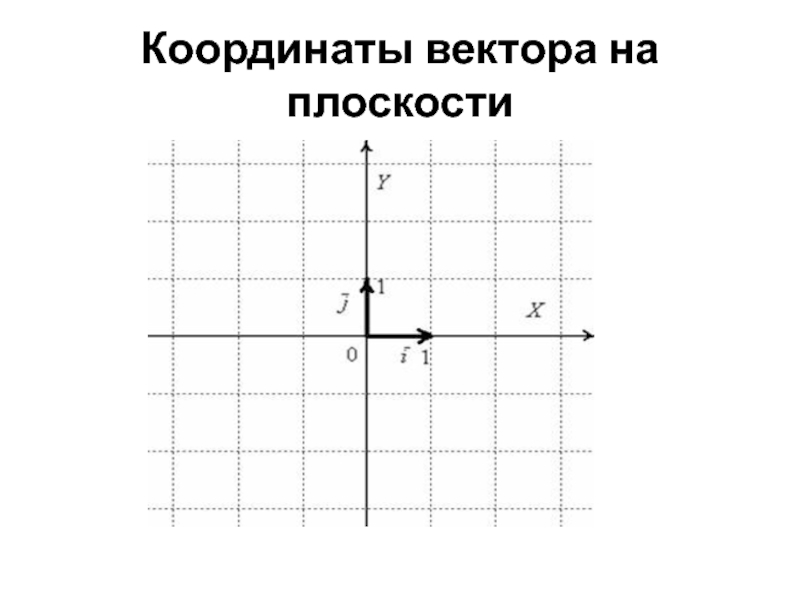
- 24. Координаты вектора на плоскости
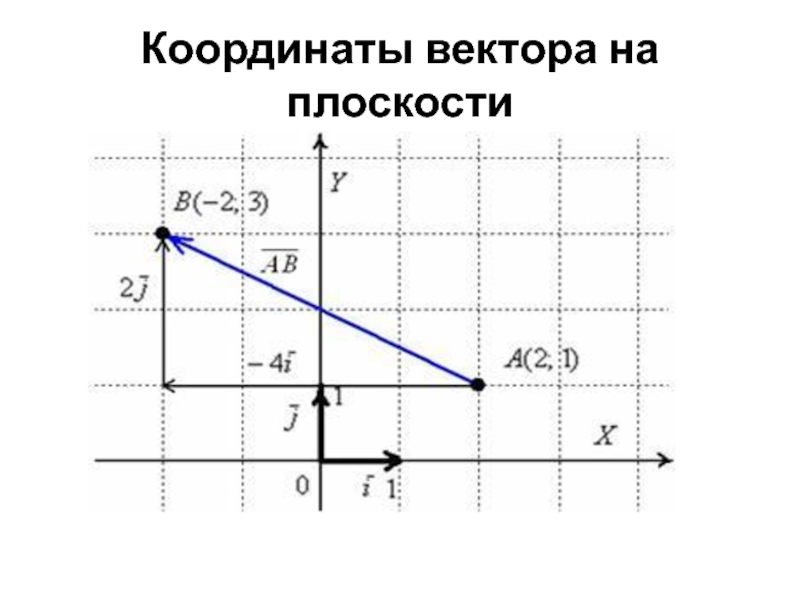
- 25. Координаты вектора на плоскости
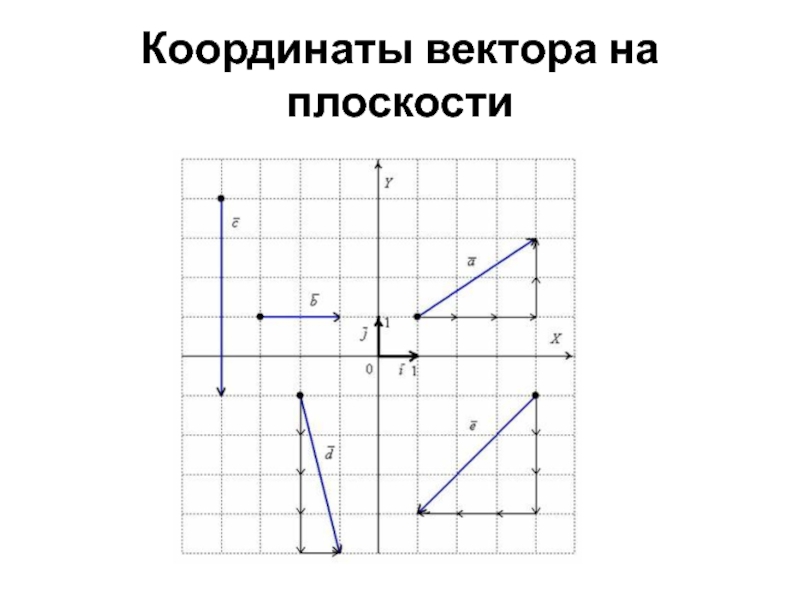
- 26. Координаты вектора на плоскости
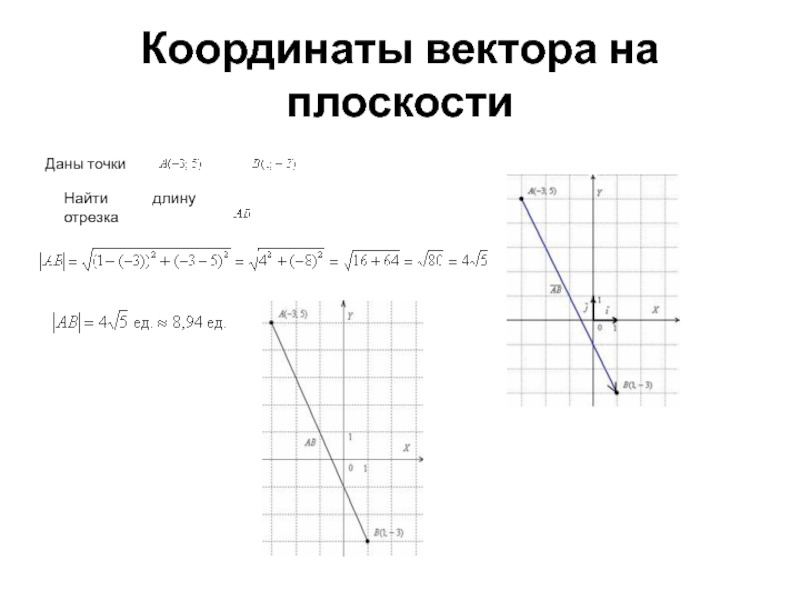
- 27. Координаты вектора на плоскости Даны точки Найти длину отрезка
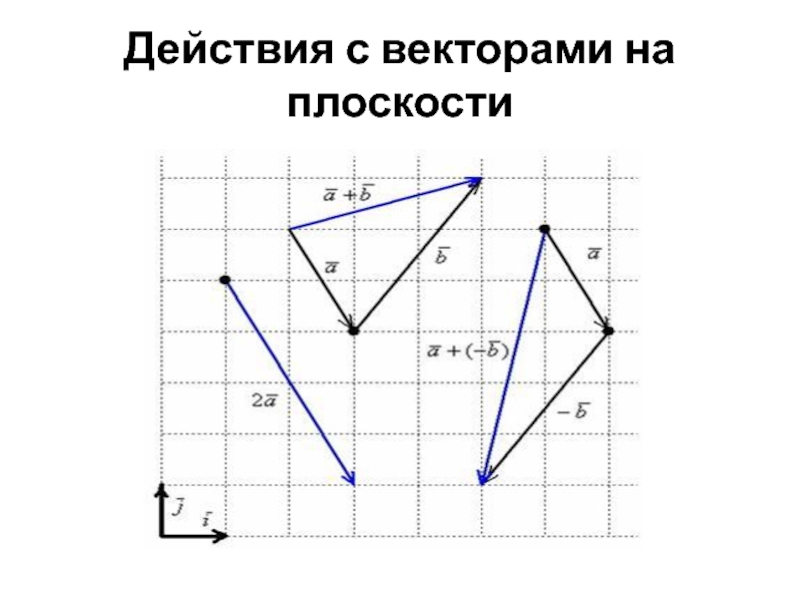
- 28. Действия с векторами на плоскости
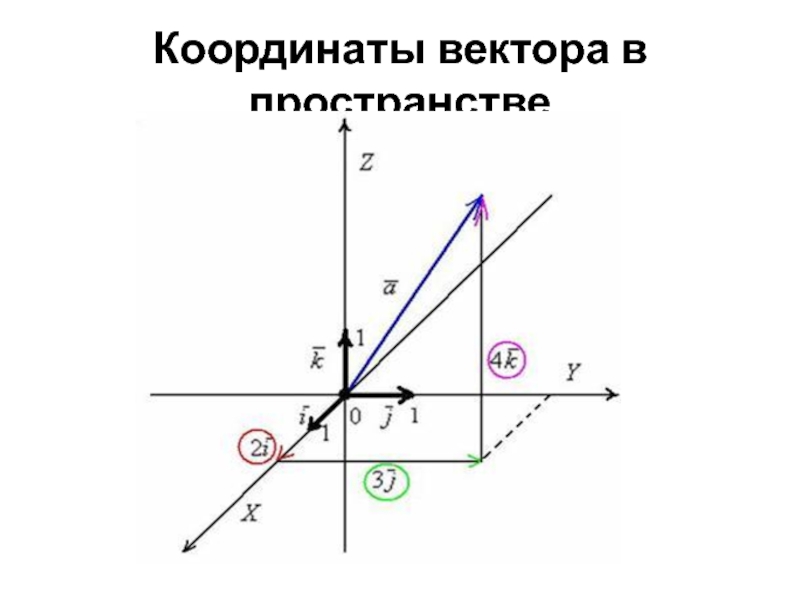
- 29. Координаты вектора в пространстве
- 30. Скалярное произведение векторов
- 31. Векторное произведение коллинеарных векторов
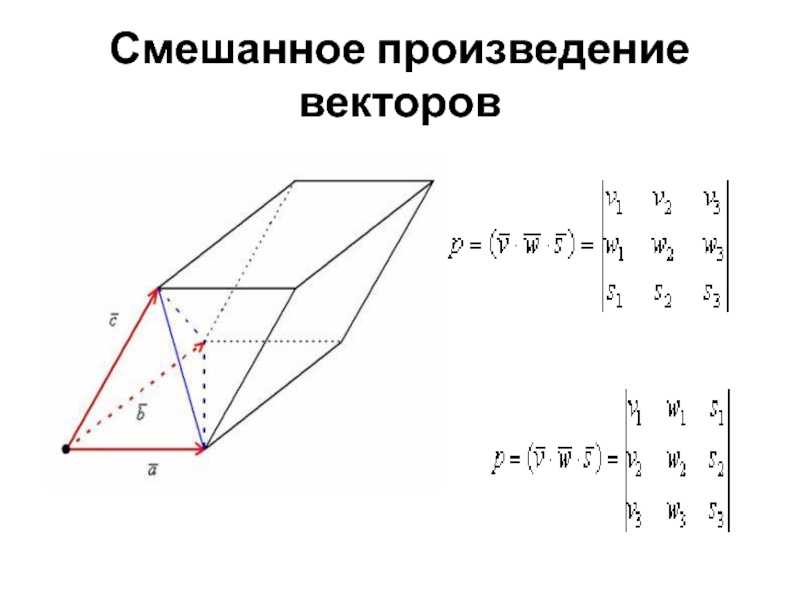
- 32. Смешанное произведение векторов
Понятие вектора Отрезок, для которого указано, какой из его концов считается началом, а какой – концом, называется вектором. Направление вектора на рисунках отмечается стрелкой. А
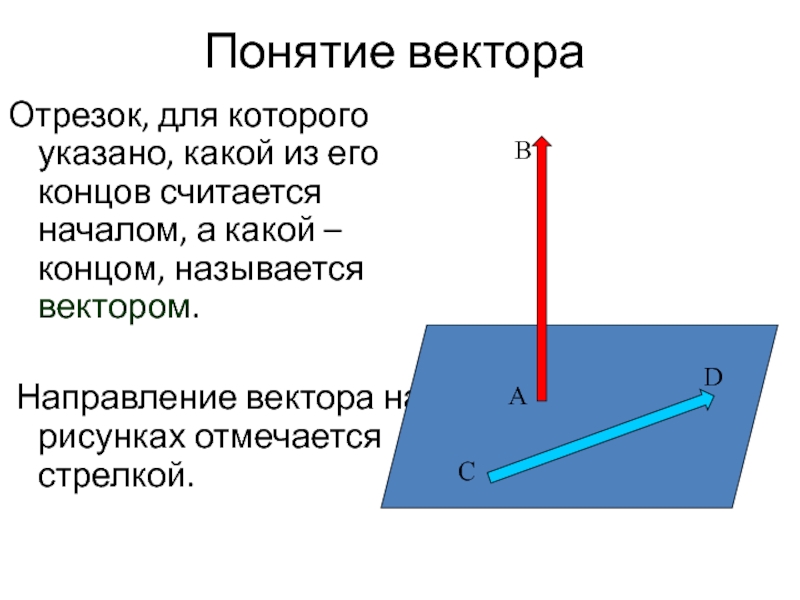
Слайд 2Понятие вектора
Отрезок, для которого указано, какой из его концов считается началом,
а какой – концом, называется вектором.
Направление вектора на рисунках отмечается стрелкой.
Направление вектора на рисунках отмечается стрелкой.
А
В
С
D
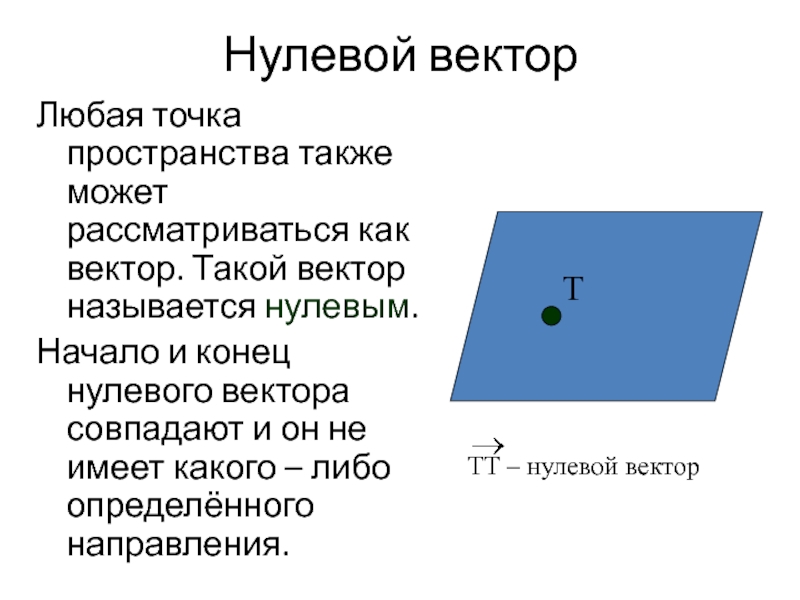
Слайд 3Нулевой вектор
Любая точка пространства также может рассматриваться как вектор. Такой вектор
называется нулевым.
Начало и конец нулевого вектора совпадают и он не имеет какого – либо определённого направления.
Начало и конец нулевого вектора совпадают и он не имеет какого – либо определённого направления.
Т
ТТ – нулевой вектор
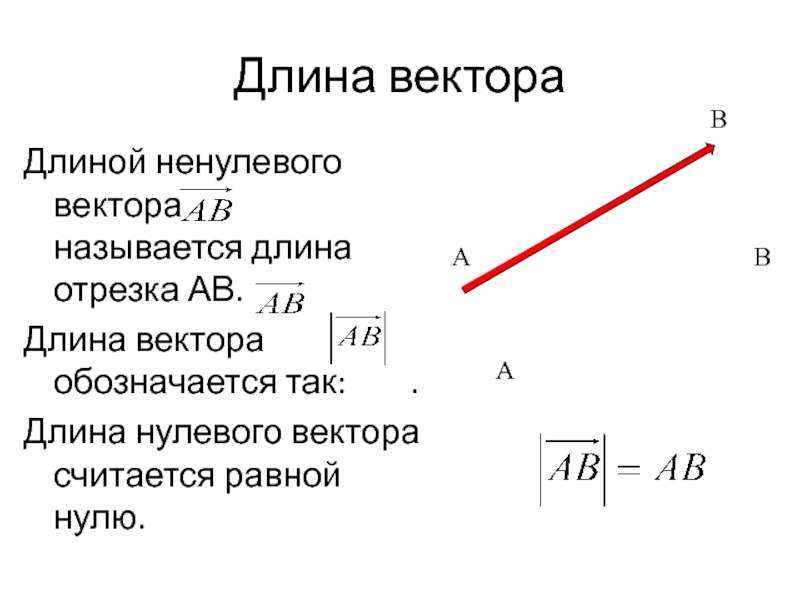
Слайд 4Длина вектора
Длиной ненулевого вектора называется длина отрезка АВ.
Длина вектора обозначается так: .
Длина нулевого вектора считается равной нулю.
А
В
А
В
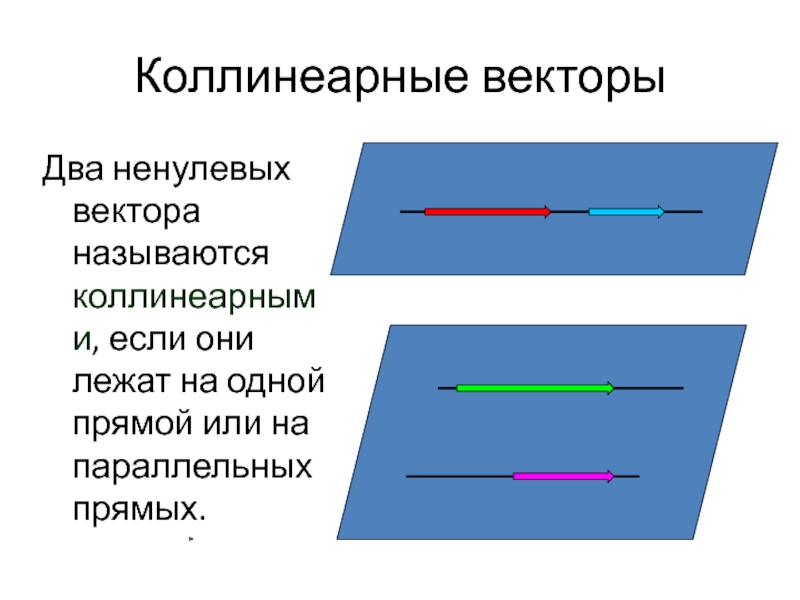
Слайд 5Коллинеарные векторы
Два ненулевых вектора называются коллинеарными, если они лежат на
одной прямой или на параллельных прямых.
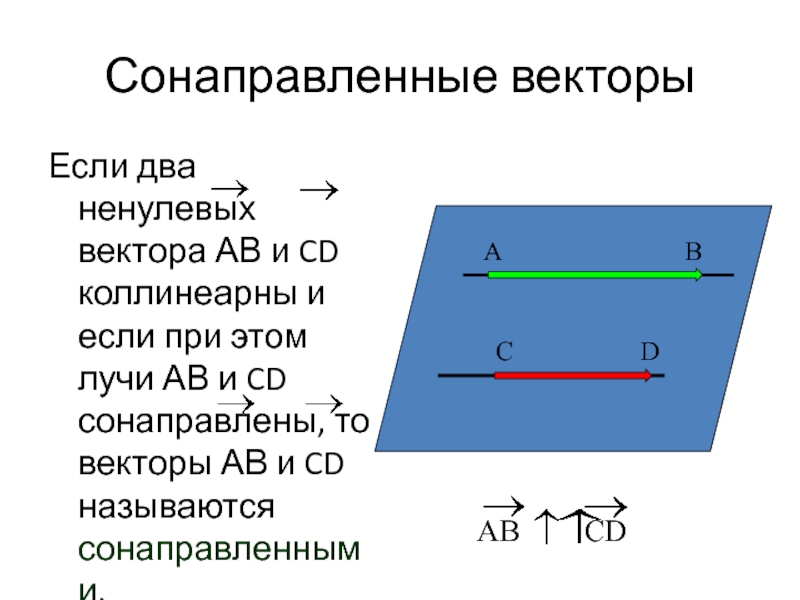
Слайд 6Сонаправленные векторы
Если два ненулевых вектора АВ и CD коллинеарны
и если при этом лучи АВ и CD сонаправлены, то векторы АВ и CD называются сонаправленными.
А
В
С
D
АВ
CD
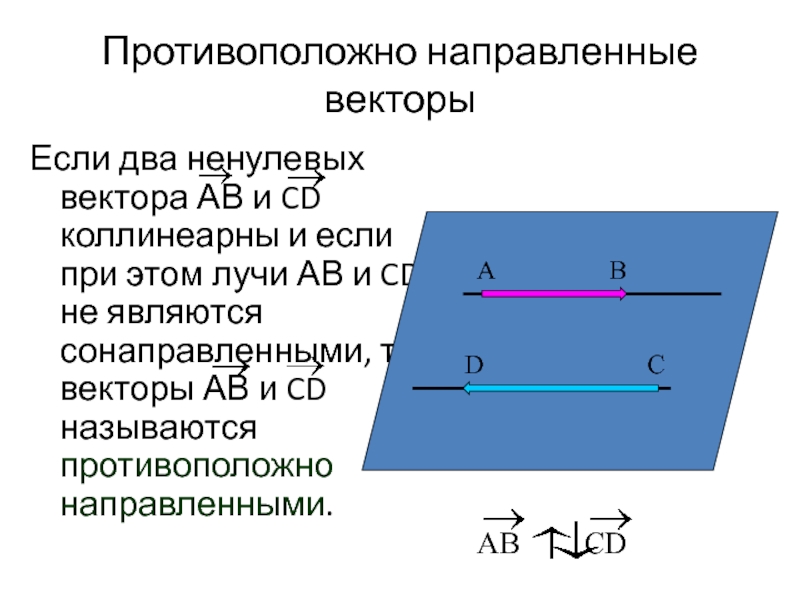
Слайд 7Противоположно направленные векторы
Если два ненулевых вектора АВ и CD коллинеарны и
если при этом лучи АВ и CD не являются сонаправленными, то векторы АВ и CD называются противоположно направленными.
А
В
С
D
АВ
СD
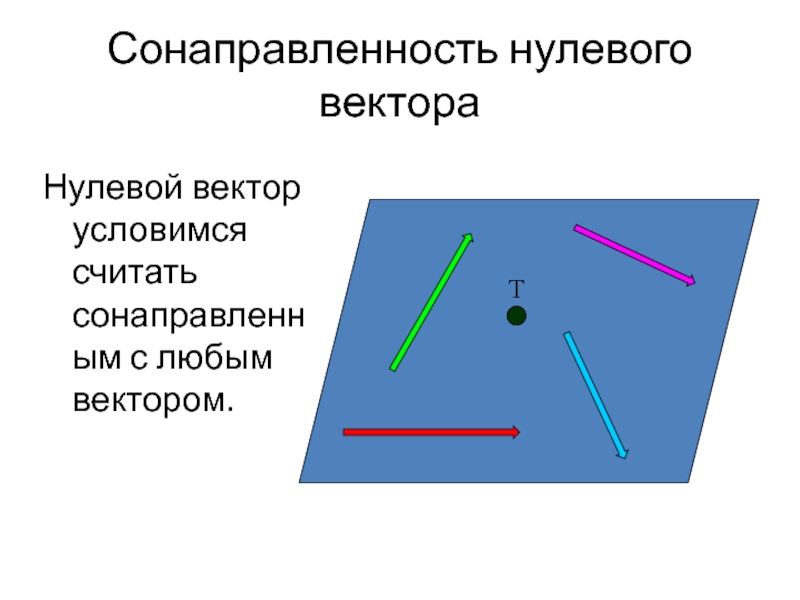
Слайд 8Сонаправленность нулевого вектора
Нулевой вектор условимся считать сонаправленным с любым вектором.
Т
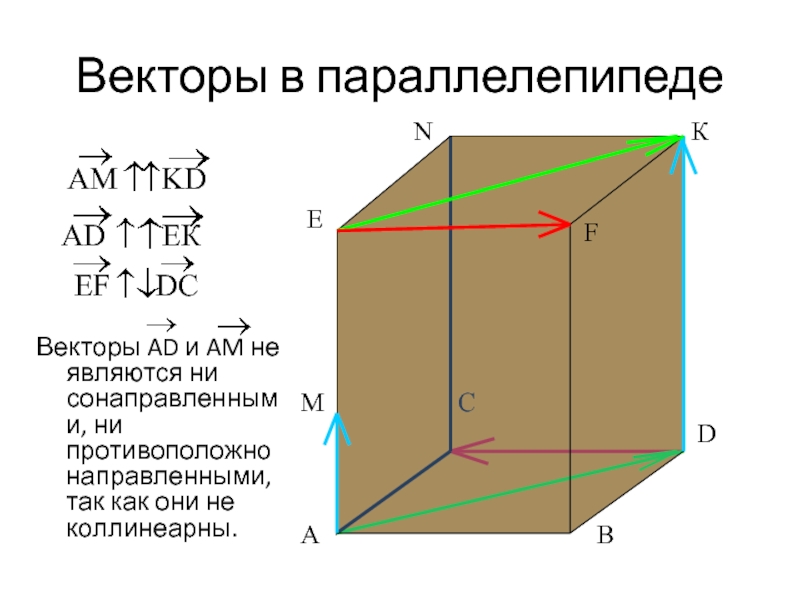
Слайд 9Векторы в параллелепипеде
Векторы AD и AM не являются ни сонаправленными, ни
противоположно направленными, так как они не коллинеарны.
С
А
В
D
М
Е
N
К
АМ
KD
AD
ЕК
F
EF
DC
Слайд 11Равенство векторов
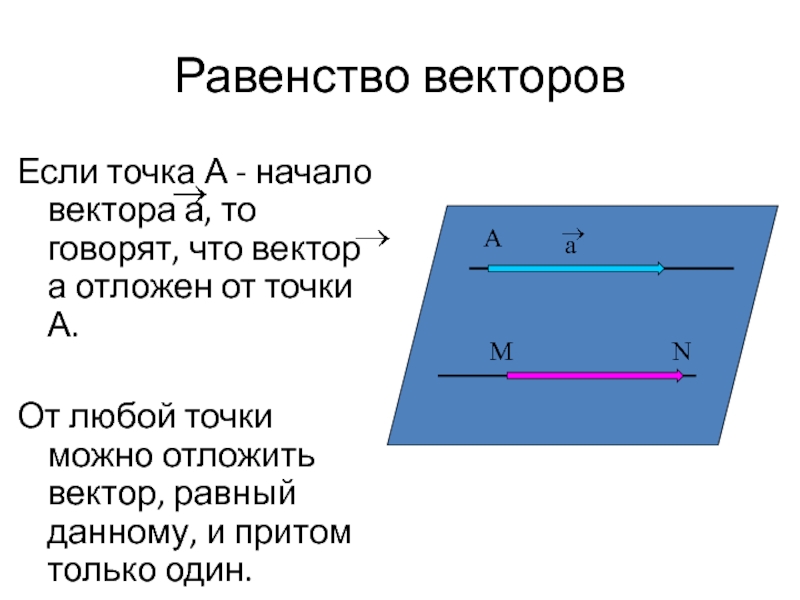
Если точка А - начало вектора а, то говорят, что
вектор а отложен от точки А.
От любой точки можно отложить вектор, равный данному, и притом только один.
От любой точки можно отложить вектор, равный данному, и притом только один.
А
а
М
N
Слайд 12Правило треугольника
Пусть а и b – два вектора. Отметим произвольную точку
А и отложим от этой точки вектор АВ, равный а. Затем от точки В отложим вектор ВС, равный b. Вектор АС называется суммой векторов а и b.
а
b
А
В
С
Слайд 13Правило параллелограмма
Чтобы сложить неколлинеарные векторы а и b, нужно отложить от
какой-нибудь точки А векторы АВ=а и АD=b и построить параллелограмм АВСD. Тогда вектор АС равен a + b.
а
b
А
В
D
С
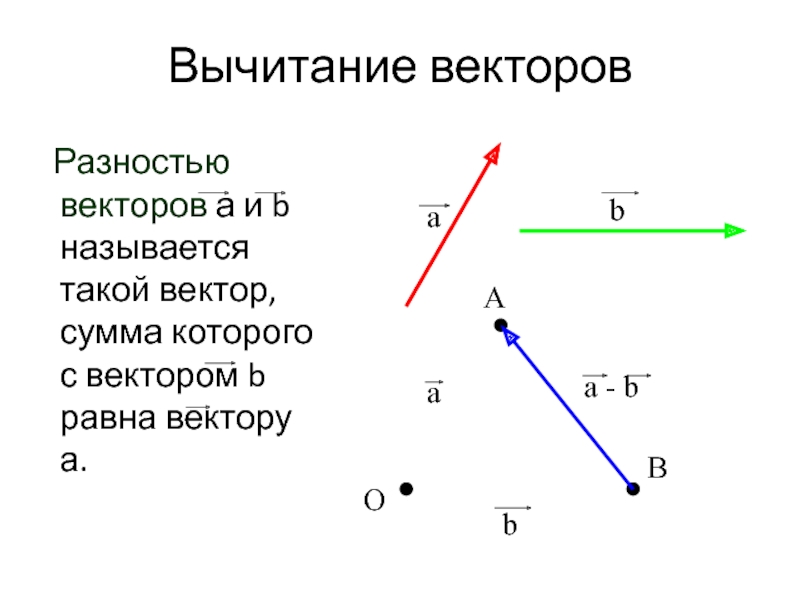
Слайд 14Вычитание векторов
Разностью векторов а и b называется такой вектор,
сумма которого с вектором b равна вектору а.
b
а
О
А
В
а
b
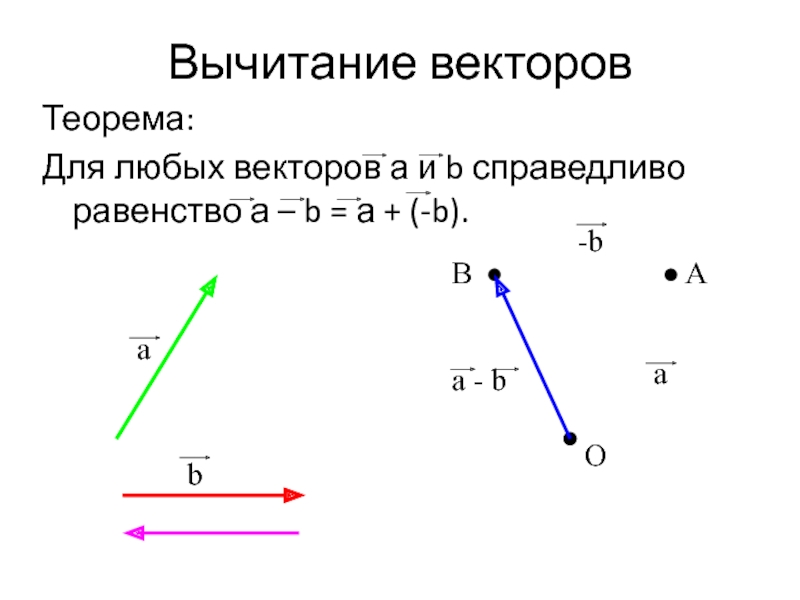
Слайд 15Вычитание векторов
Теорема:
Для любых векторов а и b справедливо равенство а
– b = а + (-b).
а
b
О
А
В
а
-b
Слайд 16Умножение вектора на число
Произведением ненулевого вектора а на число k называется
такой вектор b, длина которого равна |k|*|a|, причём векторы а и b сонаправлены при k 0 и противоположно направлены при k<0.
Произведением нулевого вектора на любое число считается нулевой вектор.
Произведением нулевого вектора на любое число считается нулевой вектор.
а
k=3
b
k = -2
-2b
Слайд 17Компланарные векторы
Векторы называются компланарными, если при откладывании их от одной и
той же точки они будут лежать в одной плоскости.
Векторы называются компланарными, если имеются равные им векторы, лежащие в одной плоскости
Векторы называются компланарными, если имеются равные им векторы, лежащие в одной плоскости
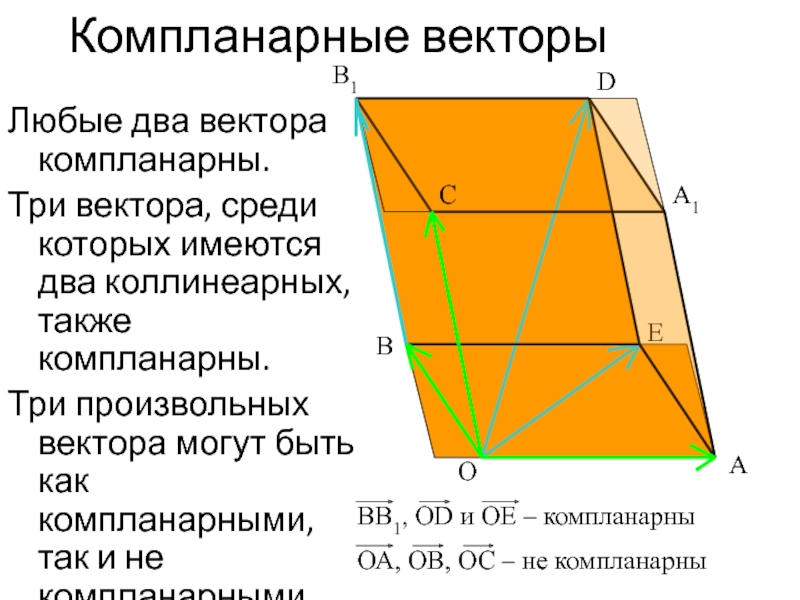
Слайд 18Компланарные векторы
Любые два вектора компланарны.
Три вектора, среди которых имеются два коллинеарных,
также компланарны.
Три произвольных вектора могут быть как компланарными, так и не компланарными.
Три произвольных вектора могут быть как компланарными, так и не компланарными.
ВВ1, ОD и ОЕ – компланарны
ОА, ОВ, ОС – не компланарны
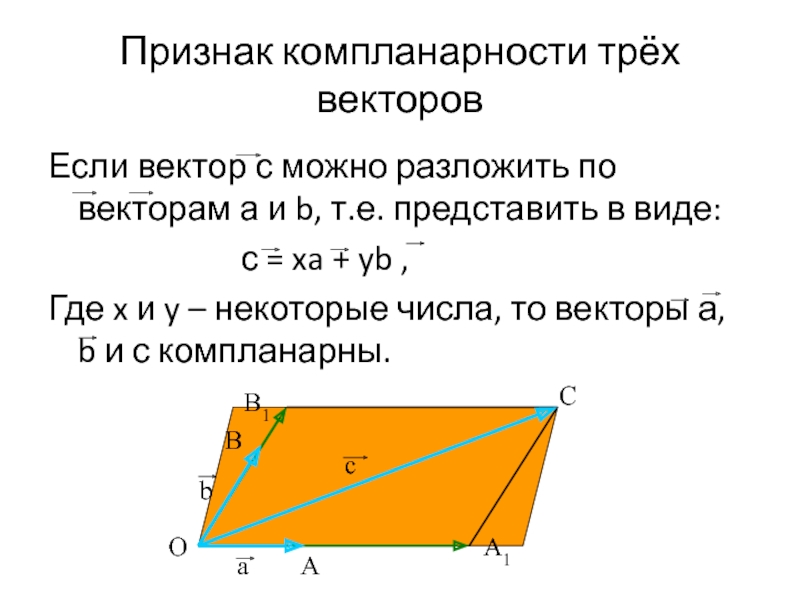
Слайд 19Признак компланарности трёх векторов
Если вектор с можно разложить по векторам а
и b, т.е. представить в виде:
с = xa + yb ,
Где x и y – некоторые числа, то векторы а, b и с компланарны.
с = xa + yb ,
Где x и y – некоторые числа, то векторы а, b и с компланарны.
О
С
А1
В1
А
В
а
b
с
Слайд 20Обратное утверждение
Если векторы а, b и с компланарны, а векторы а
и b не коллинеарны, то вектор с можно разложить по векторам а и b, причём коэффициенты разложения определяются единственным образом.
Слайд 21Правило параллелепипеда
Пусть а, b и с – некомпланарные векторы. Отложим от
произвольной точки О пространства векторы ОА = а, ОВ = b, ОС = с и построим параллелепипед так, чтобы отрезки ОА, ОВ и ОС были его рёбрами. Тогда диагональ ОD этого параллелепипеда изображает сумму векторов а, b и с: ОD = а + b + с.
Е
О
В
А
В1
С
D
А1
Слайд 22Разложение вектора по двум некомпланарным векторам
Если вектор р представлен в виде:
р = xa + yb + zc ,
где x, y и z – некоторые числа, то говорят, что вектор р разложен по векторам а, b и с. Числа x, y и z называются коэффициентами разложения.
где x, y и z – некоторые числа, то говорят, что вектор р разложен по векторам а, b и с. Числа x, y и z называются коэффициентами разложения.
Слайд 23Теорема
Любой вектор можно разложить по трём данным некомпланарным векторам, причём коэффициенты
разложения определяются единственным образом.
