τ:X × X→X декартова квадрата X2=X × X в X.
Таким образом, любой упорядоченной паре (a,b) элементов
a,b ∈X ставится в соответствие определенный элемент τ(a,b) того же множества X.
Иногда вместо τ(a,b) пишут aτb, а еще чаще бинарную операцию на X обозначают каким-нибудь специальным символом: ∗, ·, ⋅ или +.






































![Алгоритм Евклида для вычисления наибольшего общего делителяbegin g[0]: = b; g[1]: = a; i : =1; while g[i]](/img/tmb/3/212094/90bde149125994e42fd2bc813493de6e-800x.jpg)




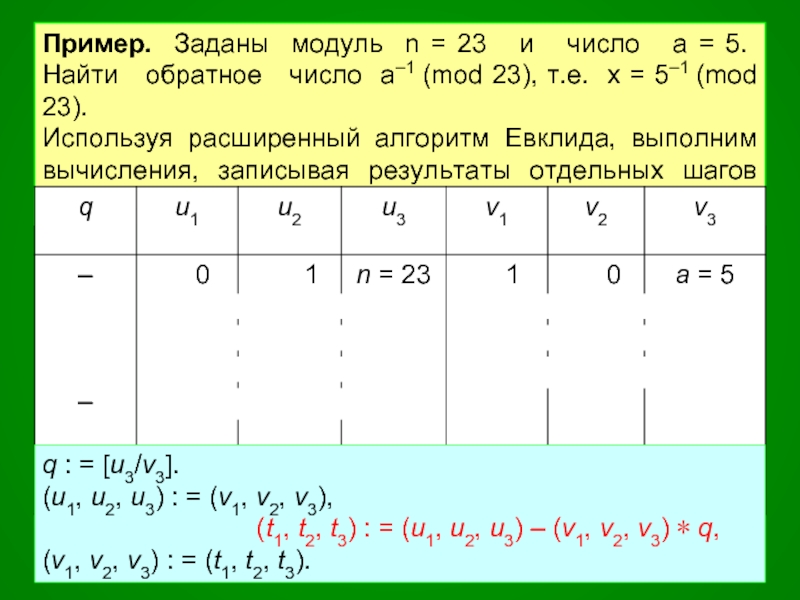







![Если функция Эйлера ϕ(n) не известна, можно использовать расширенный алгоритм Евклида.n=23 a=5 ExtendedGCD[n,a]](/img/tmb/3/212094/a1231dbe4c0a2ae96010c54001d64008-800x.jpg)
![Если функция Эйлера ϕ(n) не известна, можно использовать расширенный алгоритм Евклида.n=23 a=5 ExtendedGCD[n,a]](/img/tmb/3/212094/ef941b0653de082a653c5001c032146c-800x.jpg)







