- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Предмет математического анализа презентация
Содержание
- 1. Предмет математического анализа
- 2. Основные понятия Математический анализ – это раздел
- 3. Основные группы величин Переменные величины: скорость;
- 4. Переменные величины: Непрерывные величины – это
- 5. Обозначения: y = f (x) – функция
- 6. Функция двух переменных Пусть каждой упорядоченной паре
- 7. Основные элементарные функции: степенная функция; показательная функция; логарифмическая функция; тригонометрическая функция; обратная тригонометрическая функция.
- 9. Область определения функций
- 10. Область определения функций
- 11. Определение: Функция, составленная из основных элементарных функций
- 12. Примеры элементарных функций Примеры неэлементарных функций
- 13. СПОСОБЫ ЗАДАНИЯ ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ графический;
- 14. Спасибо за внимание!!! =)
Слайд 2Основные понятия
Математический анализ – это раздел высшей математики, в рамках которого
изучаются переменные величины и исследуются их зависимости.
Все, что может быть измерено, называют величиной.
Все, что может быть измерено, называют величиной.
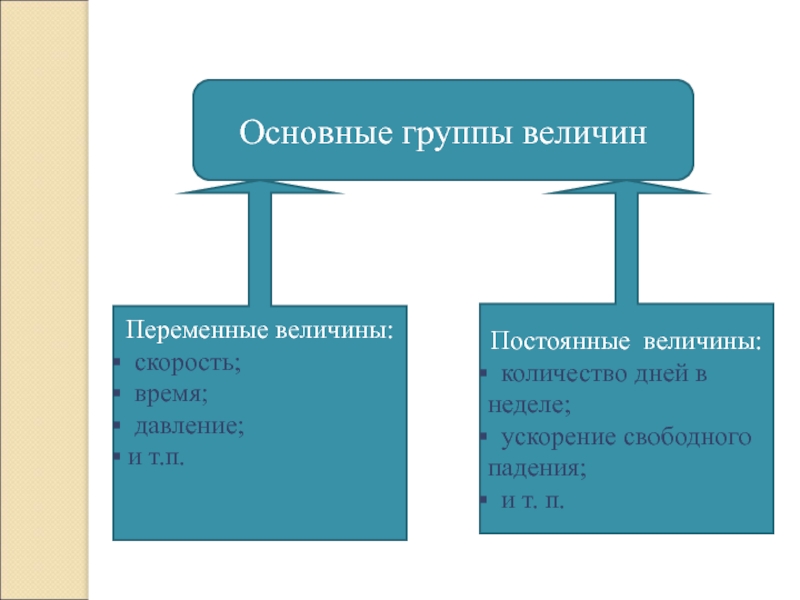
Слайд 3Основные группы величин
Переменные величины:
скорость;
время;
давление;
и т.п.
Постоянные величины:
количество дней в неделе;
ускорение свободного падения;
и т. п.
ускорение свободного падения;
и т. п.
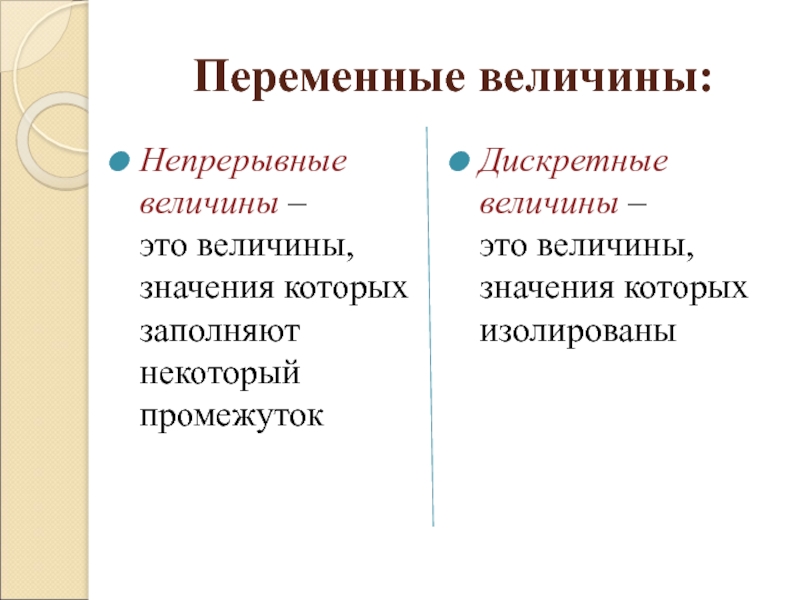
Слайд 4Переменные величины:
Непрерывные величины –
это величины, значения которых заполняют некоторый промежуток
Дискретные
величины –
это величины, значения которых изолированы
Слайд 5Обозначения:
y = f (x) – функция одной переменной;
D (y) – область
определения функции;
E (y) – множество значений функции.
E (y) – множество значений функции.
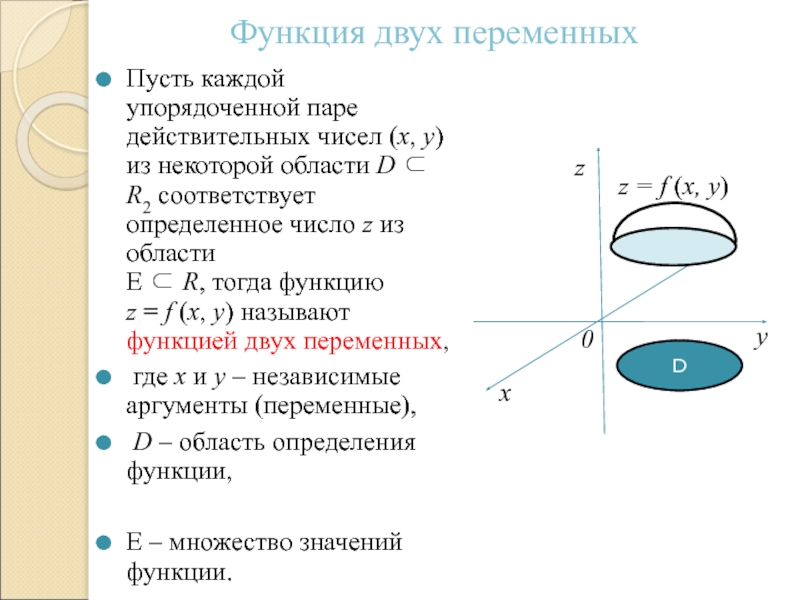
Слайд 6Функция двух переменных
Пусть каждой упорядоченной паре действительных чисел (x, y) из
некоторой области D ⊂ R2 соответствует определенное число z из области
E ⊂ R, тогда функцию
z = f (x, y) называют функцией двух переменных,
где x и y – независимые аргументы (переменные),
D – область определения функции,
E – множество значений функции.
где x и y – независимые аргументы (переменные),
D – область определения функции,
E – множество значений функции.
Слайд 7Основные элементарные функции:
степенная функция;
показательная функция;
логарифмическая функция;
тригонометрическая функция;
обратная тригонометрическая функция.
Слайд 11Определение:
Функция, составленная из основных элементарных функций называется элементарной, если:
в своей области
определения она задается одним аналитическим выражением;
она получена с помощью конечного числа арифметических операций.
она получена с помощью конечного числа арифметических операций.
Слайд 13СПОСОБЫ ЗАДАНИЯ ФУНКЦИИ
ОДНОЙ ПЕРЕМЕННОЙ
графический;
табличный;
аналитический:
а) явный вид:
у = f (x),
б) неявный вид: F (x, y) = 0,
в) параметрический вид:
б) неявный вид: F (x, y) = 0,
в) параметрический вид: