- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Тройные интегралы. Вычисление объема тела презентация
Содержание
- 1. Тройные интегралы. Вычисление объема тела
- 2. Понятие тройного интеграла вводиться аналогично понятию двойного интеграла.
- 3. Тройной интеграл в общем виде записывается следующим
- 4. Как решать тройной интеграл? Пример 1.
- 5. 3)Выбираем порядок обхода тела: Двигаемся по OZ
- 6. Пример 2. Вычислить с помощью тройного интеграла
- 7. Составим порядок обхода тела: Двигаемся по OZ
- 8. Пример 3. Вычислить с помощью тройного
- 9. Проекция тела на плоскость XOY представляет собой круг,
- 10. Пример 4. С помощью тройного интеграла вычислить
- 11. Решаем методом
Слайд 2Понятие тройного интеграла вводиться аналогично понятию двойного интеграла.
Пусть функция f(x,y,z) определена в
ограниченной замкнутой области T, которая принадлежит трехмерному пространству с определенной декартовой системой координат Oxyz. Разобьем заданную область на n частей, которые не имеют общих внутренних точек и объемы которых равны соответственно.
В каждой такой элементарной области возьмем произвольную точку Pi(xi,yi,zi)
n
составим интегральную сумму ∑f(xi,yi,zi)dVi
i=1
В каждой такой элементарной области возьмем произвольную точку Pi(xi,yi,zi)
n
составим интегральную сумму ∑f(xi,yi,zi)dVi
i=1
Слайд 3Тройной интеграл в общем виде записывается следующим образом:
f(x,y,z) – подынтегральная функция трех
переменных.
dxdydz – произведение дифференциалов.
T – область интегрирования – пространственное тело ограниченное множеством поверхностей.
Вычислить тройной интеграл – это значит найти ЧИСЛО:
В соответствии с общим смыслом интегрирования, произведение dxdydz равно бесконечно малому объему dV элементарного тела.
Тройной интеграл объединяет все эти бесконечно малые частички по области , в результате чего получается интегральное (суммарное) значение объёма тела:
dxdydz – произведение дифференциалов.
T – область интегрирования – пространственное тело ограниченное множеством поверхностей.
Вычислить тройной интеграл – это значит найти ЧИСЛО:
В соответствии с общим смыслом интегрирования, произведение dxdydz равно бесконечно малому объему dV элементарного тела.
Тройной интеграл объединяет все эти бесконечно малые частички по области , в результате чего получается интегральное (суммарное) значение объёма тела:
Слайд 4Как решать тройной интеграл?
Пример 1.
С помощью тройного интеграла вычислить объем
тела, ограниченного поверхностями Варианты ответа:
1) 2) 3) 4)
С помощью тройного интеграла вычислить объем тела, ограниченного поверхностями
1)используем формулу Сначала изобразим параллельную ортогональную проекцию тела на координатную плоскость XOY.
2) выясняем, чем тело ограничено с сверху, чем снизу и выполняем пространственный чертёж.
z=y² параболический цилиндр расположенный
над плоскостью XOY и проходящий через
ось OX:
1) 2) 3) 4)
С помощью тройного интеграла вычислить объем тела, ограниченного поверхностями
1)используем формулу Сначала изобразим параллельную ортогональную проекцию тела на координатную плоскость XOY.
2) выясняем, чем тело ограничено с сверху, чем снизу и выполняем пространственный чертёж.
z=y² параболический цилиндр расположенный
над плоскостью XOY и проходящий через
ось OX:
Слайд 53)Выбираем порядок обхода тела: Двигаемся по OZ
Двигаемся по OY =>
Двигаемся по OX
Решение свелось к двойному интегралу, используем формулу:
Ответ: 1)
Двигаемся по OX
Решение свелось к двойному интегралу, используем формулу:
Ответ: 1)
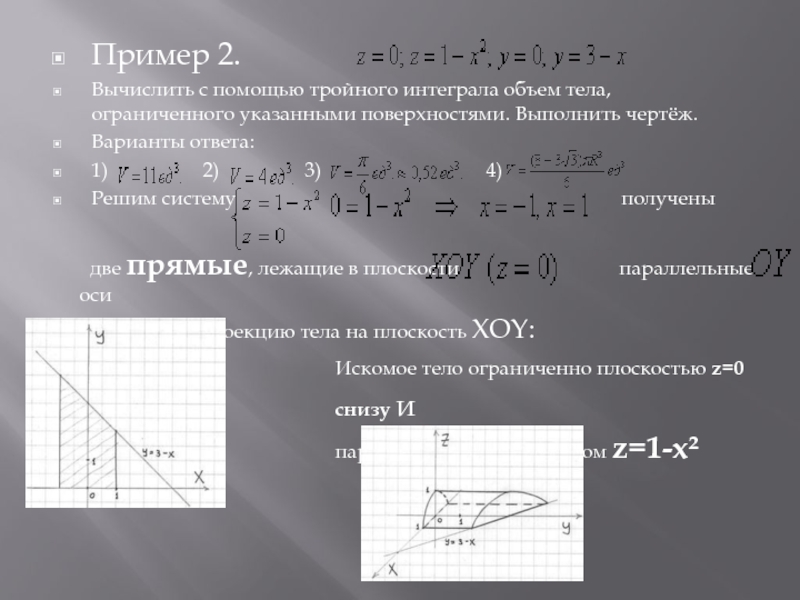
Слайд 6Пример 2.
Вычислить с помощью тройного интеграла объем тела, ограниченного указанными поверхностями.
Выполнить чертёж.
Варианты ответа:
1) 2) 3) 4)
Решим систему получены
две прямые, лежащие в плоскости параллельные оси
Изобразим проекцию тела на плоскость XOY:
Искомое тело ограниченно плоскостью z=0
снизу и
параболическим цилиндром z=1-x² сверху:
Варианты ответа:
1) 2) 3) 4)
Решим систему получены
две прямые, лежащие в плоскости параллельные оси
Изобразим проекцию тела на плоскость XOY:
Искомое тело ограниченно плоскостью z=0
снизу и
параболическим цилиндром z=1-x² сверху:
Слайд 7Составим порядок обхода тела: Двигаемся по OZ
Двигаемся по OY
Двигаемся по OX
При интегрировании по «игрек» – «икс» считается константой, поэтому константу целесообразно сразу вынести за знак интеграла.
Ответ: 2)
Двигаемся по OX
При интегрировании по «игрек» – «икс» считается константой, поэтому константу целесообразно сразу вынести за знак интеграла.
Ответ: 2)
Слайд 8Пример 3.
Вычислить с помощью тройного интеграла объём тела, ограниченного поверхностями
Выполнить чертёжи данного тела и его проекции на плоскость XOY.
Варианты отета:
1) 2) 3) 4)
Решение: придерживаемся того же порядка действий: в первую очередь рассматриваем уравнения, в которых отсутствует переменная «зет». Оно здесь одно. Проекция цилиндрической поверхности на плоскость
представляет собой «одноимённую» окружность.
Плоскости ограничивают искомое тело снизу и сверху («высекают» его из цилиндра) и проецируются в круг
Плоскость пересекает цилиндр под косым углом, в результате чего получается эллипс.
Из уравнения вычислим значения функции («высоту») в напрашивающихся точках
Варианты отета:
1) 2) 3) 4)
Решение: придерживаемся того же порядка действий: в первую очередь рассматриваем уравнения, в которых отсутствует переменная «зет». Оно здесь одно. Проекция цилиндрической поверхности на плоскость
представляет собой «одноимённую» окружность.
Плоскости ограничивают искомое тело снизу и сверху («высекают» его из цилиндра) и проецируются в круг
Плоскость пересекает цилиндр под косым углом, в результате чего получается эллипс.
Из уравнения вычислим значения функции («высоту») в напрашивающихся точках
Слайд 9Проекция тела на плоскость XOY представляет собой круг, и это весомый аргумент
в пользу перехода к цилиндрической системе координат:
Найдём уравнения поверхностей в цилиндрических координатах:
порядок обхода тела:
Ответ: 3)
Найдём уравнения поверхностей в цилиндрических координатах:
порядок обхода тела:
Ответ: 3)
Слайд 10Пример 4.
С помощью тройного интеграла вычислить объём заданного тела:
, где – произвольное положительное число.
неравенство задаёт шар с центром в начале координат радиуса , а неравенство – «внутренность» кругового цилиндра с осью симметрии радиуса . Таким образом, искомое тело ограничено круговым цилиндром сбоку и симметричными относительно плоскости сферическими сегментами сверху и снизу.
Варианты ответа:
1) 2) 3) 4)
Порядок обхода:
неравенство задаёт шар с центром в начале координат радиуса , а неравенство – «внутренность» кругового цилиндра с осью симметрии радиуса . Таким образом, искомое тело ограничено круговым цилиндром сбоку и симметричными относительно плоскости сферическими сегментами сверху и снизу.
Варианты ответа:
1) 2) 3) 4)
Порядок обхода: