- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Задания №13 базового уровня на вычисление элементов составных многогранников и площади их поверхности презентация
Содержание
- 1. Задания №13 базового уровня на вычисление элементов составных многогранников и площади их поверхности
- 2. Задания №13 базового уровня на
- 3. Содержание Задача №1 Задача №2 Задача
- 4. Задача №1 Найдите расстояние между
- 5. Задача №2 Найдите квадрат расстояния между вершинами D
- 6. Задача №3 Найдите расстояние между вершинами В1 и
- 7. Задача №4 Найдите угол CAD2 многогранника, изображенного на
- 8. Задача №5 Найдите угол АВD многогранника, изображенного
- 9. Найдите угол D2EF многогранника, изображенного на
- 10. Найдите угол EAD2 многогранника, изображенного на
- 11. Задача №8 Найдите
- 12. Найдите тангенс угла С2С3В2 многогранника, изображенного
- 13. Найдите тангенс угла АВВ3 многогранника, изображенного
- 14. Задача №11 Найдите квадрат расстояния между вершинами В2
- 15. Задача №12 Найдите квадрат расстояния между вершинами В
- 16. Задача №13 Найдите квадрат расстояния между вершинами А
- 17. Задача №14 Найдите квадрат расстояния между вершинами D
- 18. Задача №15 Найдите площадь поверхности многогранника, изображенного
- 19. Задача №16 Найдите площадь поверхности многогранника, изображенного
- 20. Задача №17 Найдите площадь поверхности многогранника, изображенного
- 21. Задача №18 Найдите площадь поверхности многогранника, изображенного
- 22. Задача №19 Найдите площадь поверхности многогранника, изображенного
- 23. Задача №20 Найдите площадь поверхности многогранника, изображенного
- 24. Задача №21 Найдите площадь поверхности многогранника, изображенного
- 25. Задача №22 Найдите площадь поверхности многогранника, изображенного
- 26. Задача №23 Найдите площадь поверхности пространственного креста,
- 27. Задачи для самостоятельного решения
- 28. Задача №1 Решите самостоятельно 1) Найдите
- 29. Задача №1 Решите самостоятельно 2) Найдите
- 30. Задача №1 Решите самостоятельно 3) Найдите
- 31. Задача №2 Решите самостоятельно Найдите квадрат
- 32. Задача №5 Решите самостоятельно Найдите угол
- 33. Задача №8 Решите самостоятельно Найдите тангенс
- 34. Задача №15 Решите самостоятельно Найдите площадь поверхности
- 35. Задача №20 Решите самостоятельно Найдите площадь поверхности
- 36. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые). Ответ: 162
- 37. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые). Ответ:
- 38. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые). Ответ:124
- 39. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые). Ответ: 84
- 40. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые). Ответ:48
- 41. Используемые ресурсы Шаблон подготовила учитель русского языка
Слайд 2Задания №13
базового уровня
на вычисление элементов
составных многогранников
и площади
Слайд 3 Содержание
Задача №1
Задача №2
Задача №3
Задача №4
Задача №5
Задача №6
Задача №7
Задача №8
Задача №9
Задача
Задача №11
Задача №12
Задача №13
Задача №14
Задача №15
Задача №16
Задача №17
Задача №18
Задача №19
Задача №20
Задача №21
Задача №22
Задача №23
Для сам. реш.
Слайд 4Задача №1
Найдите расстояние между вершинами А и С2 многогранника, изображенного на
Решение.
По теореме Пифагора имеем:
Слайд 5Задача №2
Найдите квадрат расстояния между вершинами D и С2 многогранника, изображенного на
Решение.
Рассмотрим прямоугольный треугольник DD2C2. По теореме Пифагора
Слайд 6Задача №3
Найдите расстояние между вершинами В1 и D2 многогранника, изображенного на рисунке.
Решение.
Треугольник KD2B1 = прямоуг. По теореме Пифагора:
Слайд 7Задача №4
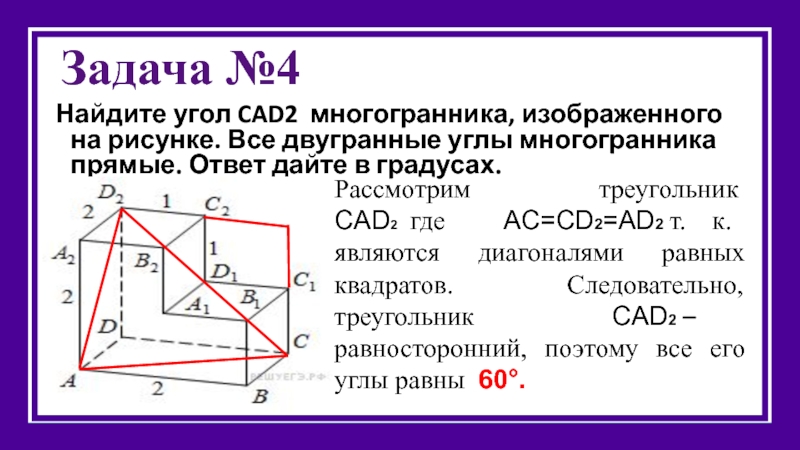
Найдите угол CAD2 многогранника, изображенного на рисунке. Все двугранные углы многогранника
Решение.
Рассмотрим треугольник CAD2 где AC=CD2=AD2 т. к. являются диагоналями равных квадратов. Следовательно, треугольник CAD2 – равносторонний, поэтому все его углы равны 60°.
Слайд 8Задача №5
Найдите угол АВD многогранника, изображенного на рисунке. Все двугранные углы
Решение.
ABCD квадрат со стороной 2, а BD — его диагональ. Значит, треугольник ABD — прямоугольный и равнобедренный, AB=AD . Угол ABD равен 45°
Слайд 9
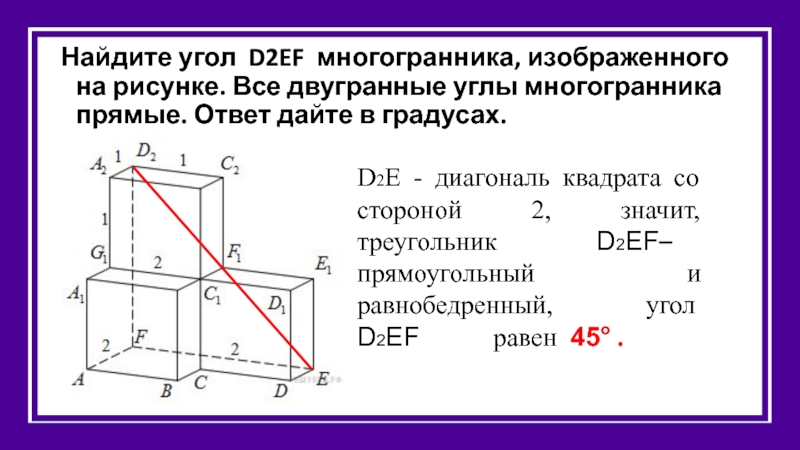
Найдите угол D2EF многогранника, изображенного на рисунке. Все двугранные углы многогранника
D2E - диагональ квадрата со стороной 2, значит, треугольник D2EF– прямоугольный и равнобедренный, угол D2EF равен 45° .
Слайд 10
Найдите угол EAD2 многогранника, изображенного на рисунке. Все двугранные углы многогранника
Рассмотрим треугольник EAD2. В нем AE=ED2=D2A, т.к. это диагонали равных квадратов.
Таким образом, треугольник EAD2 — равносторонний, все его углы равны 60°.
Слайд 11Задача №8
Найдите тангенс угла В2А2С2 многогранника, изображенного
Решение.
Треугольник В2А2С2 прямоугольный.
Значит
Слайд 12
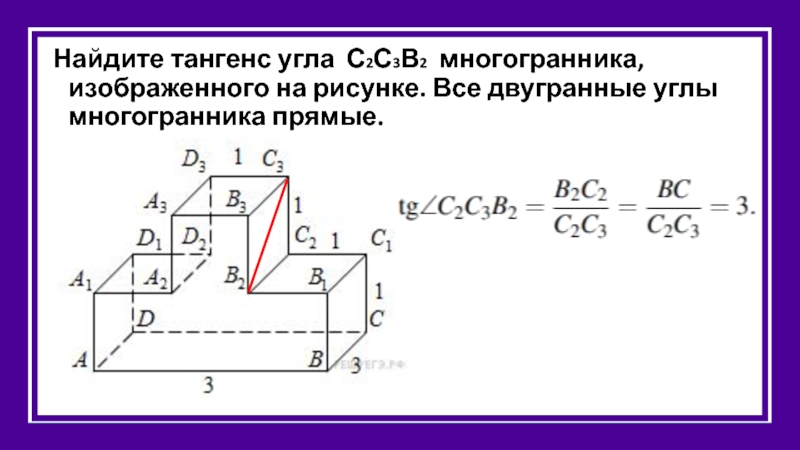
Найдите тангенс угла С2С3В2 многогранника, изображенного на рисунке. Все двугранные углы
Слайд 13
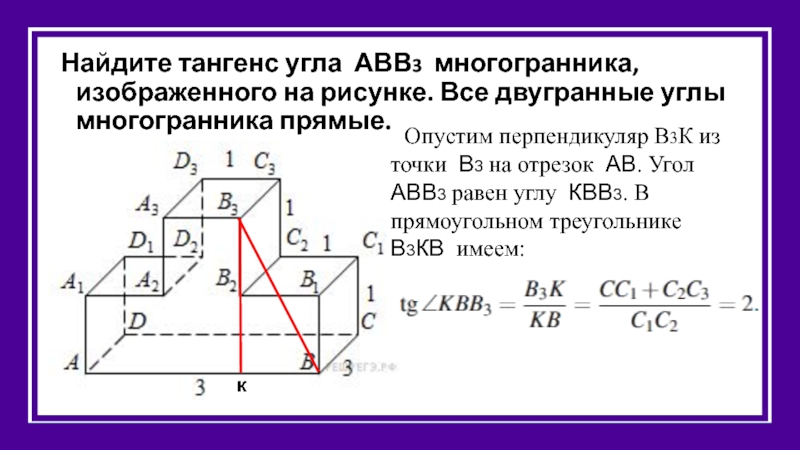
Найдите тангенс угла АВВ3 многогранника, изображенного на рисунке. Все двугранные углы
к
Опустим перпендикуляр В3К из точки В3 на отрезок АВ. Угол АВВ3 равен углу КВВ3. В прямоугольном треугольнике В3КВ имеем:
Слайд 14Задача №11
Найдите квадрат расстояния между вершинами В2 и D3 многогранника, изображенного на рисунке.
Решение.
Ответ: 11
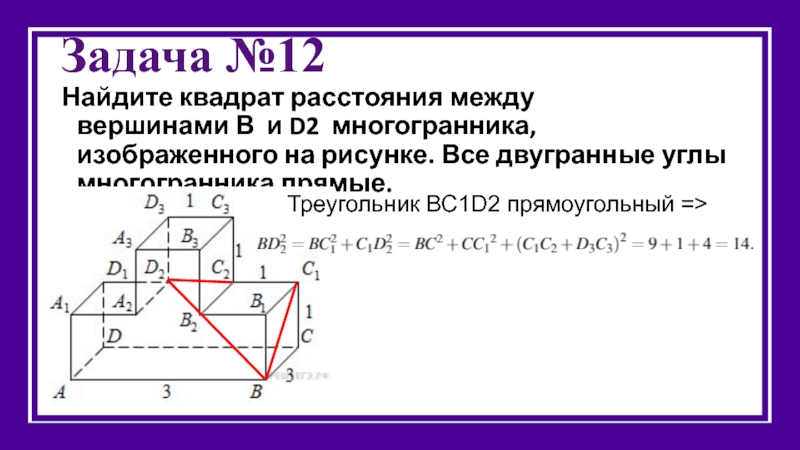
Слайд 15Задача №12
Найдите квадрат расстояния между вершинами В и D2 многогранника, изображенного на рисунке.
Решение.
Треугольник ВС1D2 прямоугольный =>
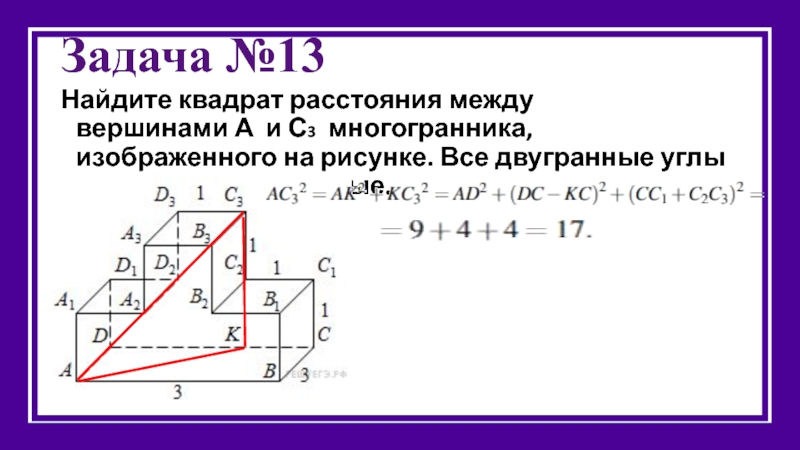
Слайд 16Задача №13
Найдите квадрат расстояния между вершинами А и С3 многогранника, изображенного на рисунке.
Решение.
Слайд 17Задача №14
Найдите квадрат расстояния между вершинами D и С2 многогранника, изображенного на рисунке.
Слайд 18Задача №15
Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы
Площадь поверхности заданного многогранника равна разности площади поверхности прямоугольного параллелепипеда с ребрами
2, 3, 1 и двух площадей прямоугольников со сторонами 2, 1:
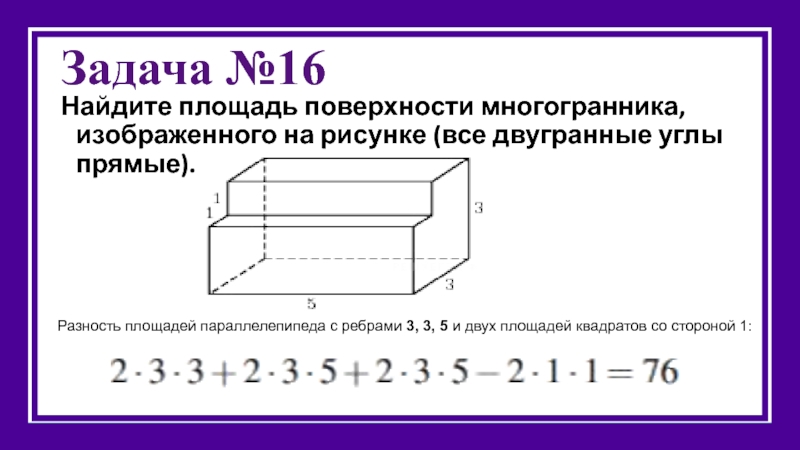
Слайд 19Задача №16
Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы
Разность площадей параллелепипеда с ребрами 3, 3, 5 и двух площадей квадратов со стороной 1:
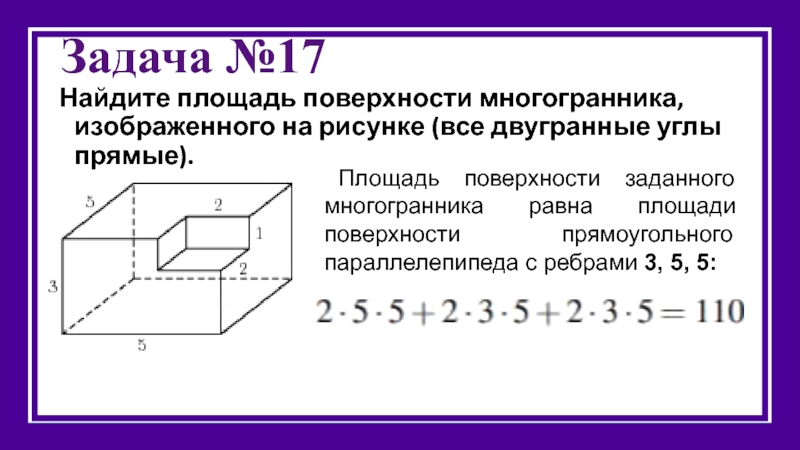
Слайд 20Задача №17
Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы
Площадь поверхности заданного многогранника равна площади поверхности прямоугольного параллелепипеда с ребрами 3, 5, 5:
Слайд 21Задача №18
Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы
Площадь поверхности заданного многогранника равна площади поверхности прямоугольного параллелепипеда с ребрами 3, 5, 4:
Слайд 22Задача №19
Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы
Площадь поверхности заданного многогранника равна сумме площадей большого и маленького параллелепипедов с ребрами 1, 5, 7 и 1, 1, 2, уменьшенной на 4 площади прямоугольника со сторонами 1, 2 — передней грани маленького параллелепипеда, излишне учтенной при расчете площадей поверхности параллелепипедов:
Слайд 23Задача №20
Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы
Площадь поверхности тела равна сумме поверхностей трех составляющих ее параллелепипедов с ребрами 2,5,6; 2,5,3 и 2,2,3, уменьшенная на удвоенные площади прямоугольников со сторонами 5 ,3 и 2, 3:
Слайд 24Задача №21
Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы
Площадь поверхности данной детали - есть сумма площади поверхности двух многогранников: со сторонами 1,2,5 и 2,2,2 за вычетом 2 площадей прямоугольников со сторонами 2,2 (т. к. данная площадь учитывается два раза при сложении площадей многогранников, а как видно из рисунка, данных площадей в итоговой детали нет). Значит:
Слайд 25Задача №22
Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы
Площадь поверхности данной детали - есть площадь поверхности многогранника со сторонами 6,5,5 за вычетом площади двух "боковых прямоугольников" со сторонами 3,2 и прибавления 2 площадей "верхнего" и "нижнего прямоугольников" со сторонами 2,5. Получаем:
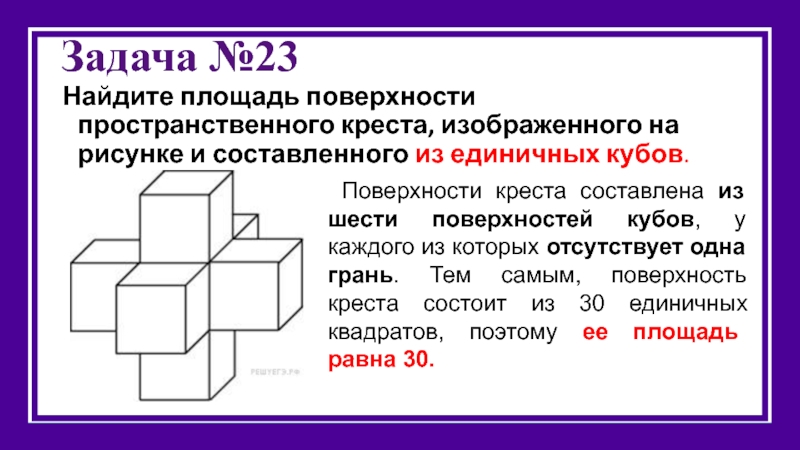
Слайд 26Задача №23
Найдите площадь поверхности пространственного креста, изображенного на рисунке и составленного
Поверхности креста составлена из шести поверхностей кубов, у каждого из которых отсутствует одна грань. Тем самым, поверхность креста состоит из 30 единичных квадратов, поэтому ее площадь равна 30.
Слайд 28Задача №1 Решите самостоятельно
1) Найдите расстояние между вершинами D и B2
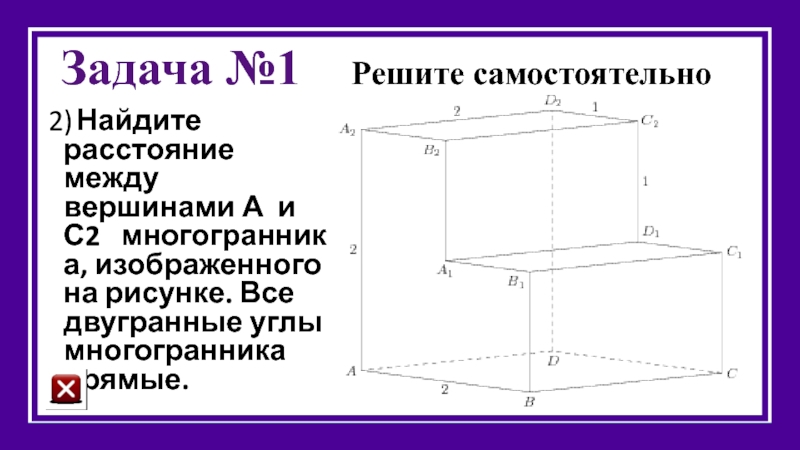
Слайд 29Задача №1 Решите самостоятельно
2) Найдите расстояние между вершинами А и С2
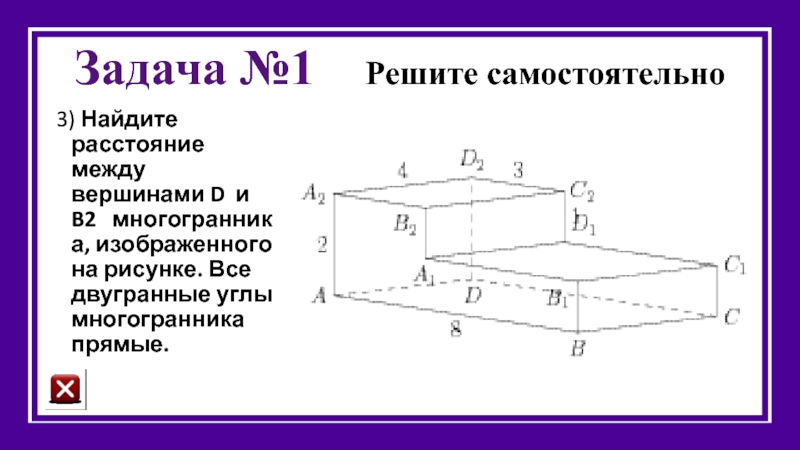
Слайд 30Задача №1 Решите самостоятельно
3) Найдите расстояние между вершинами D и B2
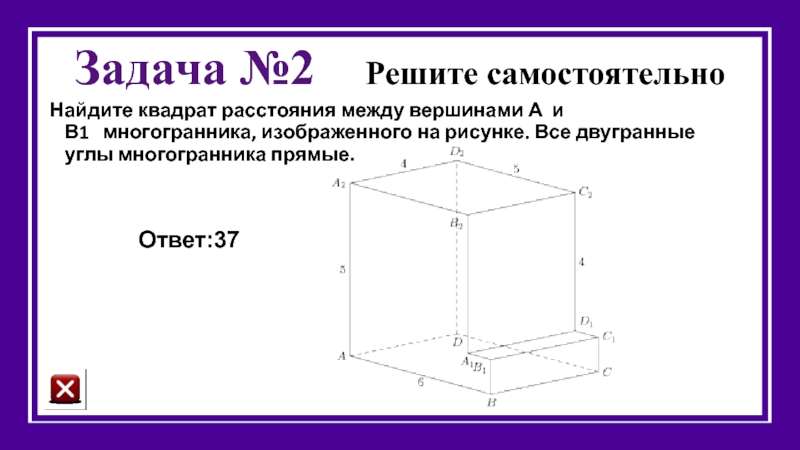
Слайд 31Задача №2 Решите самостоятельно
Найдите квадрат расстояния между вершинами А и В1
Ответ:37
Слайд 32Задача №5 Решите самостоятельно
Найдите угол АВD многогранника, изображенного на рисунке.
Ответ: 45
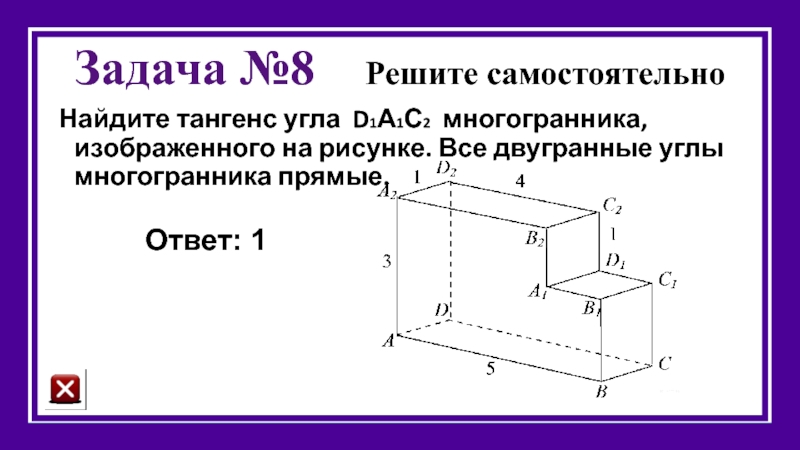
Слайд 33Задача №8 Решите самостоятельно
Найдите тангенс угла D1А1С2 многогранника, изображенного на
Ответ: 1
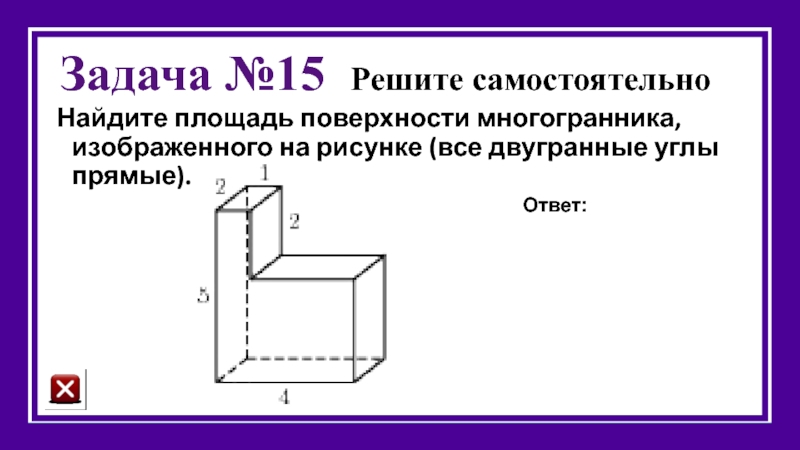
Слайд 34Задача №15 Решите самостоятельно
Найдите площадь поверхности многогранника, изображенного на рисунке (все
Ответ:
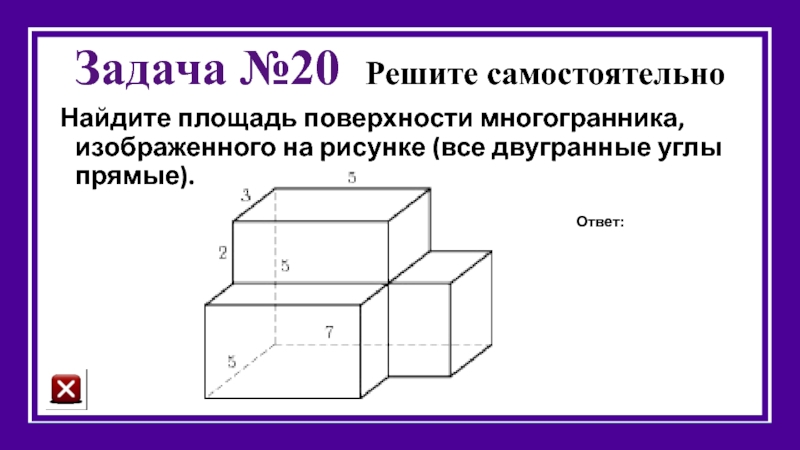
Слайд 35Задача №20 Решите самостоятельно
Найдите площадь поверхности многогранника, изображенного на рисунке (все
Ответ:
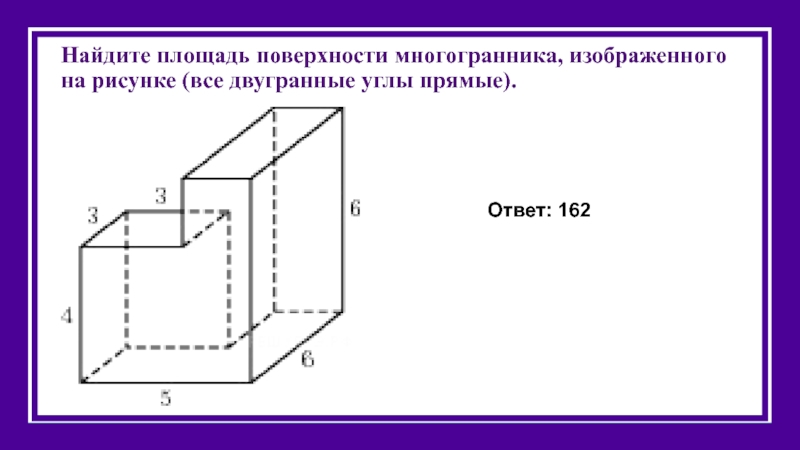
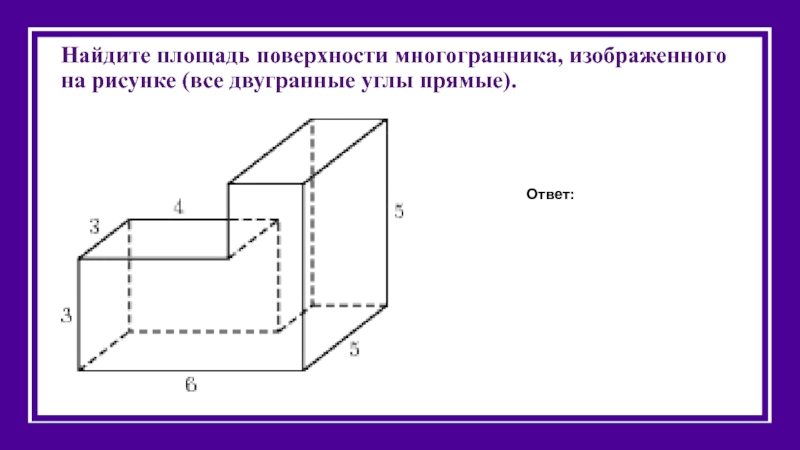
Слайд 36Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ:
Слайд 37Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ:
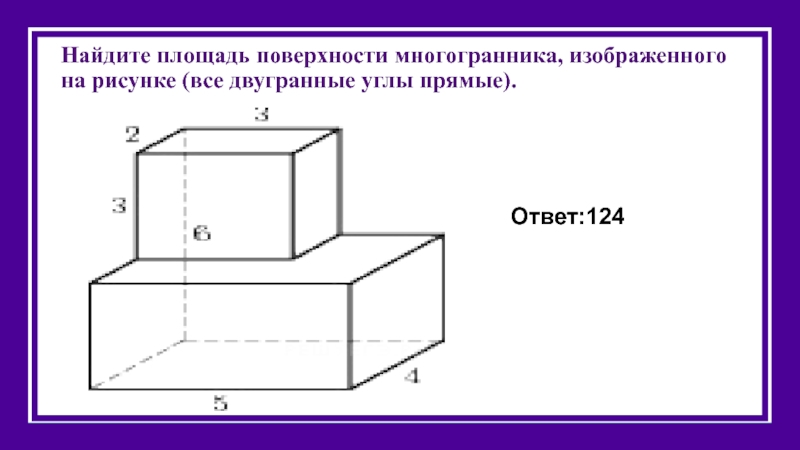
Слайд 38Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ:124
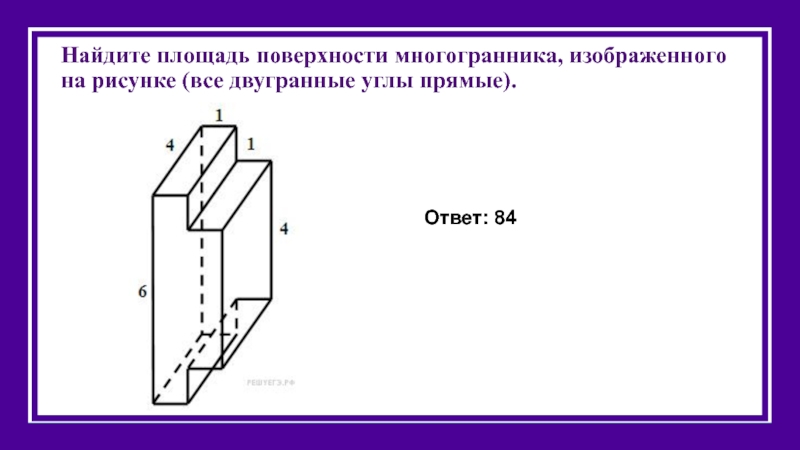
Слайд 39Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ:
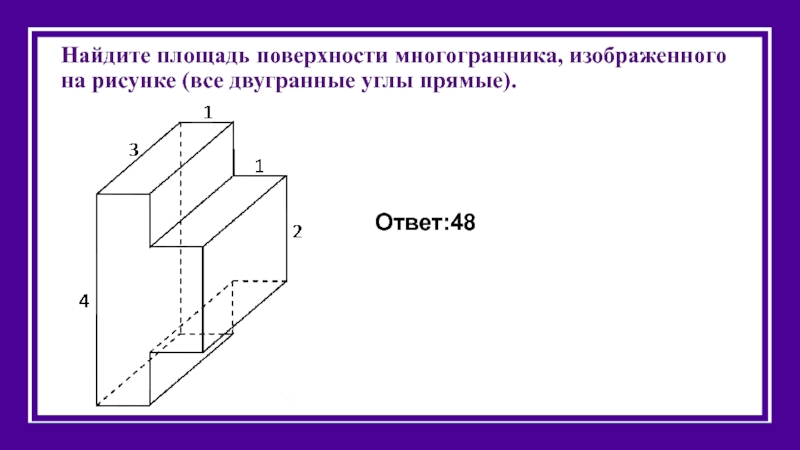
Слайд 40Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Ответ:48
Слайд 41Используемые ресурсы
Шаблон подготовила учитель русского языка и литературы Тихонова Надежда Андреевна
http://sch-53.ru/files/director/GIA/2016/%D0%95%D0%93%D0%AD%202016.jpg
«Решу
http://lib2.znate.ru/pars_docs/refs/324/323424/323424_html_m22f8f945.gif
Автор и источник заимствования неизвестен