- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
ЛА-УП-Л1 презентация
Содержание
- 1. ЛА-УП-Л1
- 2. Введение Контакты Лектор: Фаизова Анна Андреевна, ассистент каф. Управления рисками и страхования a.faizova@spbu.ru faizova.anna@gmail.com
- 3. Введение Матрицы. Определители. Обратные матрицы Системы
- 4. Введение Основная З.И.Боревич. Определители и матрицы.М.2004.
- 5. Введение Письменные контрольные работы (1 и 2).
- 6. Введение Теоретическая часть: знание всех определений
- 7. Введение Экзамен письменный. 10 заданий: 5 теоретических
- 8. ШКАЛА ОЦЕНОК «отлично» (A) – 90-100 баллов,
- 9. Линейная алгебра Лекция 1 Матрицы. Действия над матрицами
- 10. 30.09.2015 Матрицы ПЛАН ЛЕКЦИИ Матрицы. Матрицы специального
- 11. МАТРИЦЫ. Пример. Матрицы Матрицей размера m
- 12. Матрицы специального вида КВАДРАТНАЯ МАТРИЦА Если число
- 13. Матрицы специального вида Пусть А – квадратная
- 14. Матрицы специального вида ДИАГОНАЛЬНАЯ МАТРИЦА Квадратная матрица
- 15. Матрицы специального вида ЕДИНИЧНАЯ МАТРИЦА Для квадратных
- 16. Пусть A – квадратная матрица. Если
- 17. Операции над матрицами СЛОЖЕНИЕ МАТРИЦ Суммой A+B
- 18. 30.09.2015 Операции над матрицами УМНОЖЕНИЕ ЧИСЛА НА
- 19. Произведением АВ матрицы
- 20. 30.09.2015 Свойства операций над матрицами Для матриц,
- 21. 30.09.2015 Свойства операций над матрицами СВОЙСТВА
- 22. 30.09.2015 Матрицы СВОЙСТВО ЕДИНИЧНОЙ МАТРИЦЫ Пример:
- 23. Операции над матрицами ТРАНСПОНИРОВАНИЕ МАТРИЦ A
- 24. Свойства операций над матрицами НЕКОТОРЫЕ СВОЙСТВА ОПЕРАЦИИ ТРАНСПОНИРОВАНИЯ МАТРИЦ
Слайд 2Введение
Контакты
Лектор:
Фаизова Анна Андреевна,
ассистент каф. Управления рисками и страхования
a.faizova@spbu.ru
faizova.anna@gmail.com
Слайд 3Введение
Матрицы. Определители. Обратные матрицы
Системы линейных уравнений
Векторы
Базисы и размерность
Примеры экономических
ОСНОВНЫЕ РАЗДЕЛЫ КУРСА
Слайд 4Введение
Основная
З.И.Боревич. Определители и матрицы.М.2004.
Н.Ш.Кремер. Высшая математика для экономистов.
Д.К.Фаддеев. Лекции по алгебре.Наука.М.1984.
Учебные и контрольные задания по математике (высшая алгебра). Изд. ЭСФ СПбГУ. 2005.
Дополнительная
Н.А.Вавилов, В.Г.Халин. «MATHEMATICA 5.* для нематематика.» Выпуски 1 и 2. СПб.: ОЦЭиМ, 2005.экономике. М. 2002.
РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
Слайд 5Введение
Письменные контрольные работы (1 и 2).
Индивидуальные контрольные задания.
КОНТРОЛЬ ЗНАНИЙ
Слайд 6Введение
Теоретическая часть: знание всех определений и формулировок;
Практическая часть: навыки решения задач,
Использование пособий, учебников, конспектов и технических устройств не допускается.
ЭКЗАМЕН
Слайд 7Введение
Экзамен письменный. 10 заданий: 5 теоретических вопросов и 5 задач. Каждый
Правильное выполнение индивидуальных контрольных заданий –10 баллов (5 работ по 2 балла каждая)
Письменные контрольные работы – 20 баллов (по 10 баллов каждая)
Дополнительно:
Активность на практических занятиях, решение задач повышенной сложности, выполнение домашних заданий
3
КРИТЕРИИ ОЦЕНКИ
Слайд 8ШКАЛА ОЦЕНОК
«отлично» (A) – 90-100 баллов,
«очень хорошо» (B) – 80-89 баллов,
«хорошо»
«удовлетворительно» (D) –60-69 баллов,
«посредственно» (E) – 50-59 баллов,
«неудовлетворительно» (F) – менее 50 баллов
Слайд 1030.09.2015
Матрицы
ПЛАН ЛЕКЦИИ
Матрицы.
Матрицы специального вида.
Операции над матрицами:
сложение матриц;
умножение матрицы на число;
умножение матриц;
транспонирование
Свойства операций над матрицами.
Слайд 11 МАТРИЦЫ. Пример.
Матрицы
Матрицей размера m х n называется прямоугольная таблица из
Примеры
Определение
Обозначения:
Слайд 12Матрицы специального вида
КВАДРАТНАЯ МАТРИЦА
Если число столбцов матрицы равно числу строк (m=n),
то матрица называется квадратной.
Примеры.
Определение
Слайд 13Матрицы специального вида
Пусть А – квадратная матрица.
Если
В частности, матрица называется
верхнетреугольной, если для всех i>j,
и нижнетреугольной, если для всех i
ТРЕУГОЛЬНАЯ МАТРИЦА
Определение
Слайд 14Матрицы специального вида
ДИАГОНАЛЬНАЯ МАТРИЦА
Квадратная матрица вида
называется диагональной.
Определение
Слайд 15Матрицы специального вида
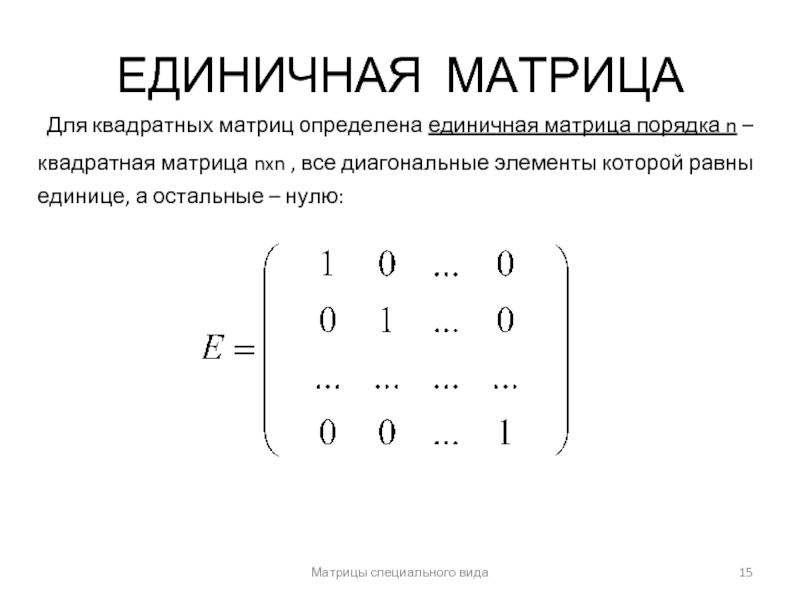
ЕДИНИЧНАЯ МАТРИЦА
Для квадратных матриц определена единичная матрица порядка n
Слайд 16Пусть A – квадратная матрица.
Если
Матрицы специального вида
СИММЕТРИЧЕСКАЯ МАТРИЦА
Определение.
Примеры
Слайд 17Операции над матрицами
СЛОЖЕНИЕ МАТРИЦ
Суммой A+B матриц размера mхn
называется матрица того же размера, каждый элемент которой равен сумме соответственных элементов матриц A и B :
Пример
Слайд 1830.09.2015
Операции над матрицами
УМНОЖЕНИЕ ЧИСЛА НА МАТРИЦУ
Произведением числа
называется матрица , получающаяся из матрицы A умножением всех ее элементов на :
Пример
Слайд 19Произведением АВ матрицы размера mхn
Операции над матрицами
УМНОЖЕНИЕ МАТРИЦ
Пример
Слайд 2030.09.2015
Свойства операций над матрицами
Для матриц, вообще говоря, АВ ≠ ВА
Пример:
НЕКОММУТАТИВНОСТЬ
Если АВ = ВА, матрицы А и В называются коммутирующими.
Слайд 2130.09.2015
Свойства операций над матрицами
СВОЙСТВА ОПЕРАЦИЙ НАД МАТРИЦАМИ
А+В = В+А
(A+B)+C = A+(B+C)
λ(A+B) = λA+λB
A(B+C) = AB + AC
(A+B)C = AC + BC
λ(AB)=(λA)B=A(λB)
А(ВС)=(АВ)С
Слайд 2230.09.2015
Матрицы
СВОЙСТВО ЕДИНИЧНОЙ МАТРИЦЫ
Пример:
Для любой квадратной матрицы А выполнено:
АЕ = ЕА
Слайд 23Операции над матрицами
ТРАНСПОНИРОВАНИЕ МАТРИЦ
A - матрица размера m x n
для A
Обозначения: .