- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Тригонометрические неравенства презентация
Содержание
Слайд 2
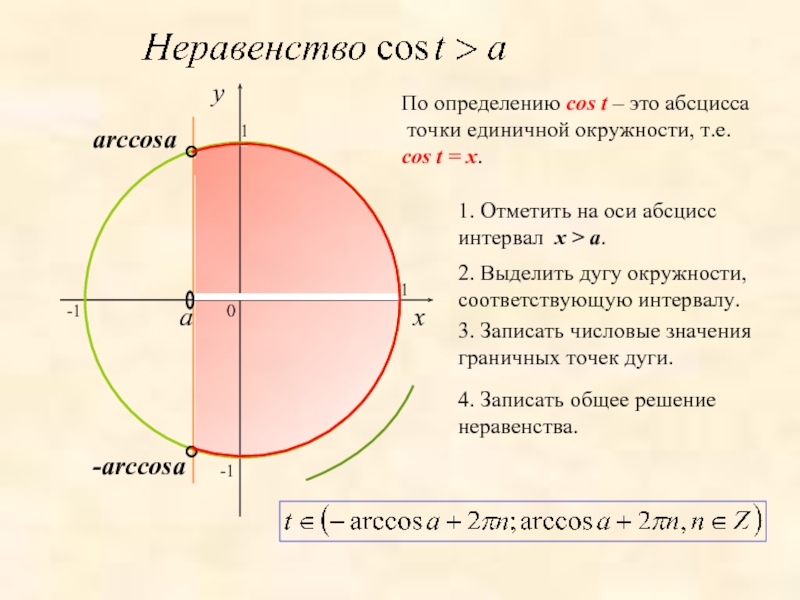
0
y
x
1. Отметить на оси абсцисс интервал x > a.
a
1
1
-1
-1
arccosa
-arccosa
2. Выделить дугу
3. Записать числовые значения граничных точек дуги.
4. Записать общее решение неравенства.
По определению cos t – это абсцисса
точки единичной окружности, т.е.
сos t = x.
Слайд 3
Решить неравенство:
1. Отметим на оси абсцисс интервал
2. Выделим дугу окружности,
3. Запишем числовые значения граничных точек дуги.
4. Запишем общее решение неравенства.
Слайд 4
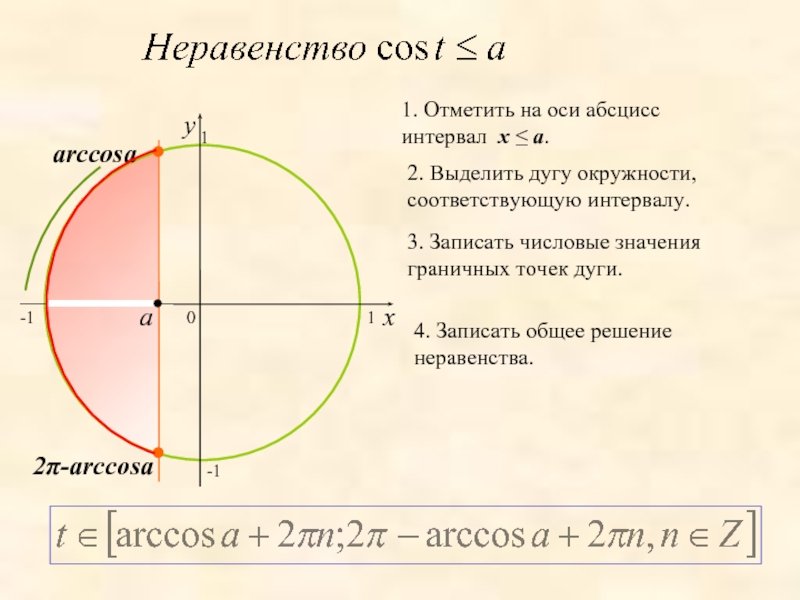
0
x
y
1. Отметить на оси абсцисс интервал x ≤ a.
2. Выделить дугу
3. Записать числовые значения граничных точек дуги.
4. Записать общее решение неравенства.
a
arccosa
2π-arccosa
-1
1
1
-1
Слайд 5
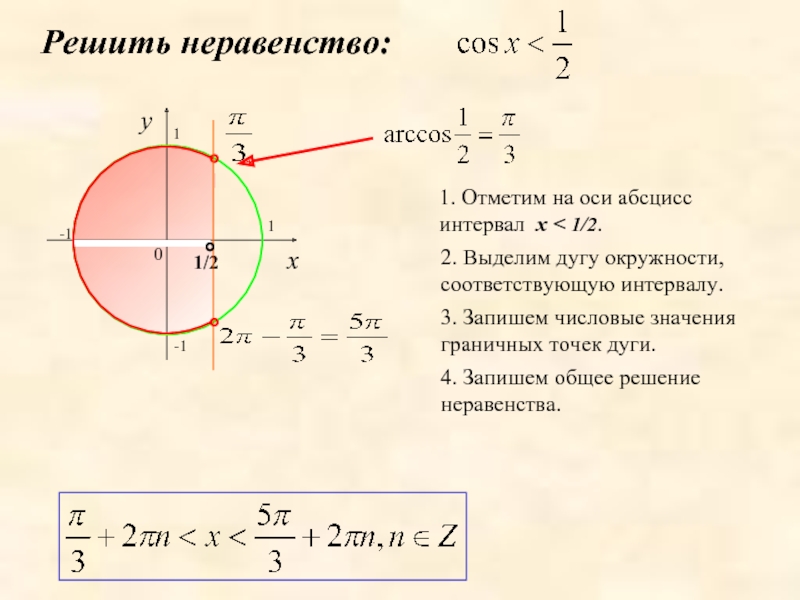
Решить неравенство:
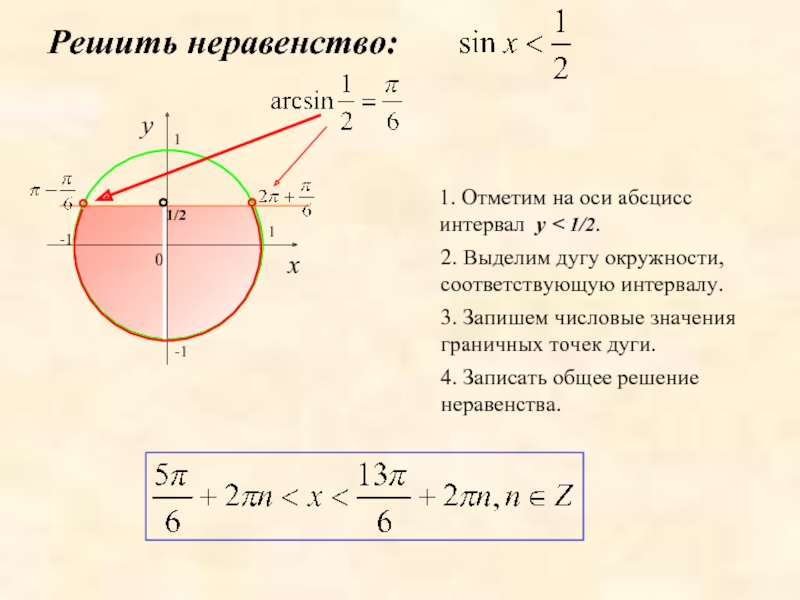
1. Отметим на оси абсцисс интервал x < 1/2.
2. Выделим
3. Запишем числовые значения граничных точек дуги.
4. Запишем общее решение неравенства.
Слайд 6
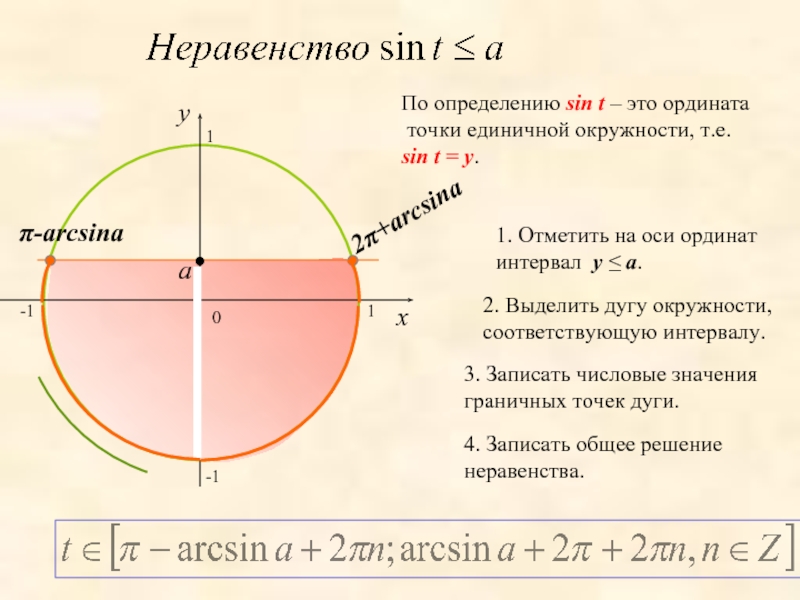
0
x
y
1. Отметить на оси ординат интервал y ≤ a.
2. Выделить дугу
3. Записать числовые значения граничных точек дуги.
4. Записать общее решение неравенства.
a
2π+arcsina
-1
1
1
-1
π-arcsina
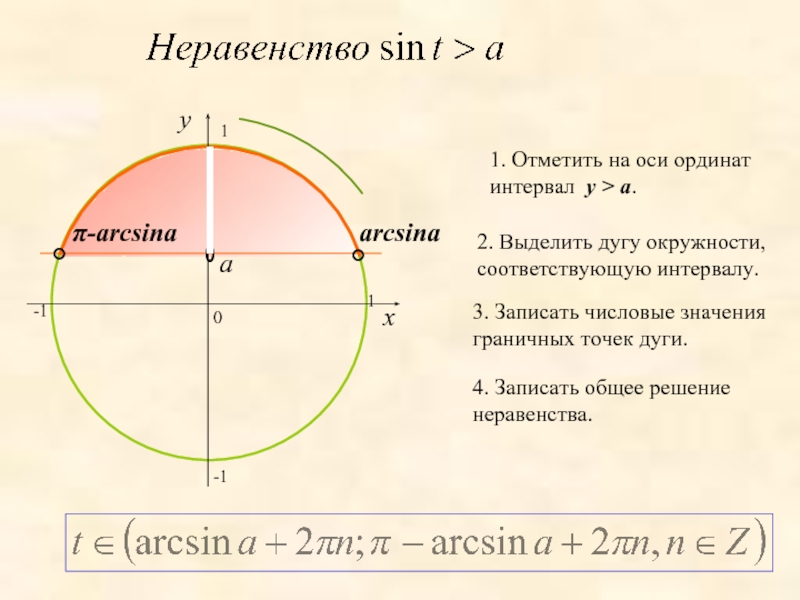
По определению sin t – это ордината
точки единичной окружности, т.е.
sin t = y.
Слайд 7
1. Отметим на оси абсцисс интервал y < 1/2.
2. Выделим дугу
3. Запишем числовые значения граничных точек дуги.
4. Записать общее решение неравенства.
Решить неравенство:
Слайд 8
0
x
y
1. Отметить на оси ординат интервал y > a.
2. Выделить дугу
3. Записать числовые значения граничных точек дуги.
4. Записать общее решение неравенства.
a
arcsina
-1
1
1
-1
π-arcsina
Слайд 9
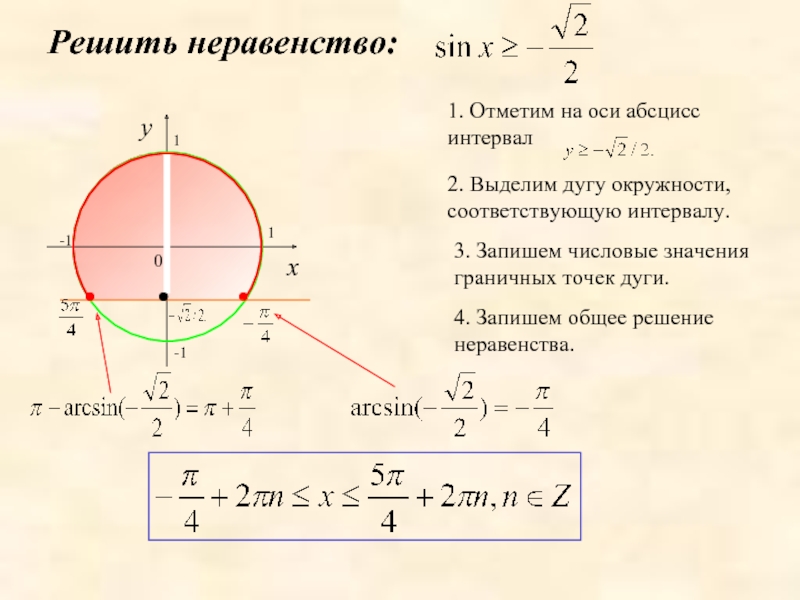
1. Отметим на оси абсцисс интервал
Решить неравенство:
2. Выделим дугу окружности,
3. Запишем числовые значения граничных точек дуги.
4. Запишем общее решение неравенства.
Слайд 10x
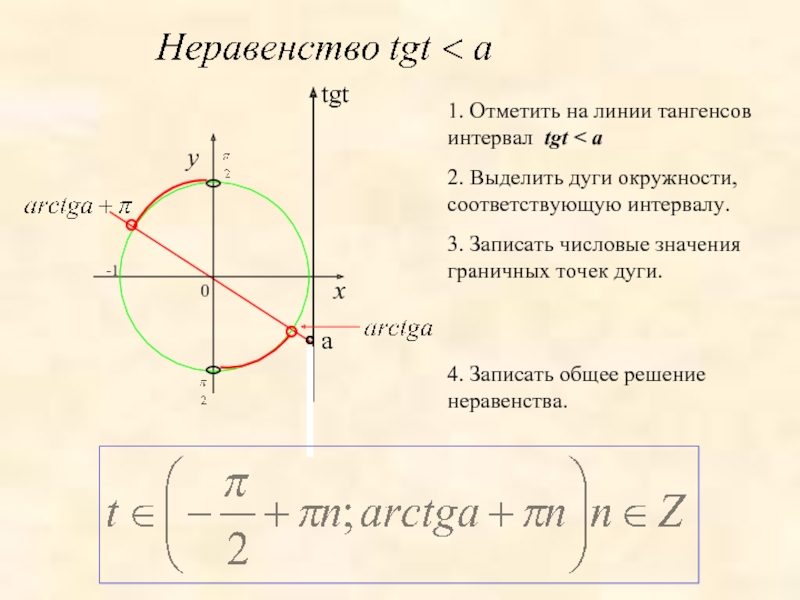
tgt
a
2. Выделить дуги окружности, соответствующую интервалу.
3. Записать числовые значения граничных точек
4. Записать общее решение неравенства.
1. Отметить на линии тангенсов интервал tgt < a
Слайд 11x
tgt
a
2. Выделить дуги окружности, соответствующую интервалу.
3. Записать числовые значения граничных точек
4. Записать общее решение неравенства.
1. Отметить на линии тангенсов интервал tgt > a
Слайд 12x
2. Выделим дуги окружности, соответствующую интервалу.
3. Запишем числовые значения граничных точек
1. Отметим на линии тангенсов интервал
tgt
Решить неравенство:
4. Запишем общее решение неравенства.
Слайд 13ctgt
a
2. Выделить дуги окружности, соответствующую интервалу.
3. Записать числовые значения граничных точек
4. Записать общее решение неравенства.
1. Отметить на линии котангенсов интервал ctgt < a
Неравенство ctgt < a
Слайд 14ctgt
a
2. Выделить дуги окружности, соответствующую интервалу.
3. Записать числовые значения граничных точек
4. Записать общее решение неравенства.
1. Отметить на линии котангенсов интервал ctgt > a
Неравенство ctgt > a
Слайд 15
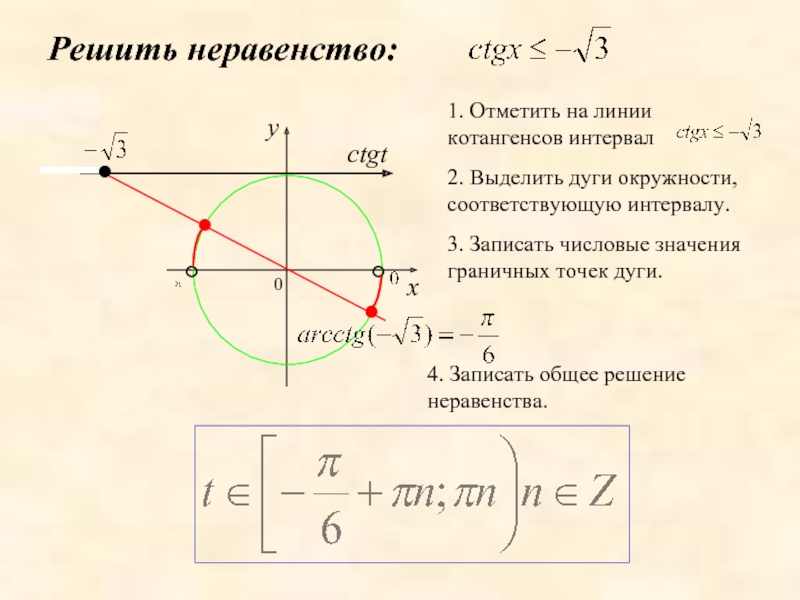
Решить неравенство:
ctgt
2. Выделить дуги окружности, соответствующую интервалу.
3. Записать числовые значения граничных
4. Записать общее решение неравенства.
1. Отметить на линии котангенсов интервал