- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Свойства медиан и биссектрисы треугольника презентация
Содержание
- 1. Свойства медиан и биссектрисы треугольника
- 2. Что такое медиана треугольника? Медиана треугольника- это
- 3. Утверждение 1. Медиана треугольника
- 4. Утверждение 2. Точка пересечения двух любых медиан
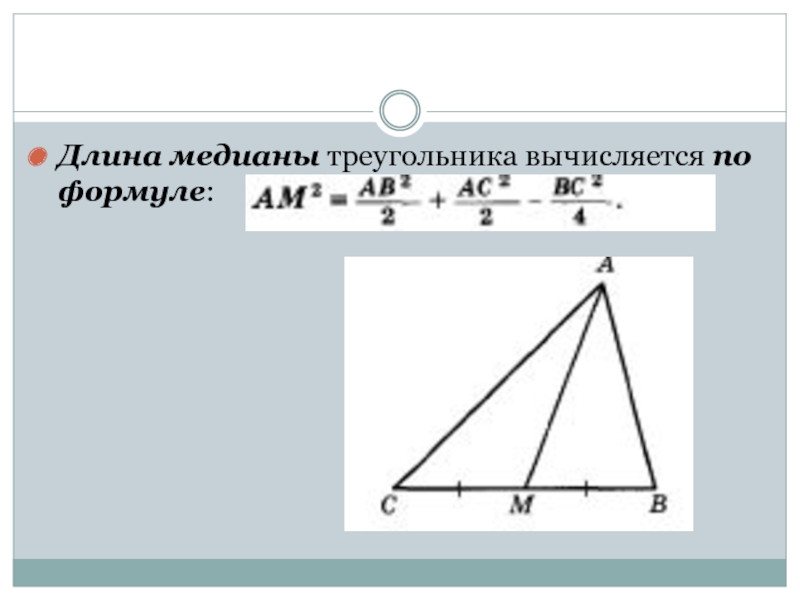
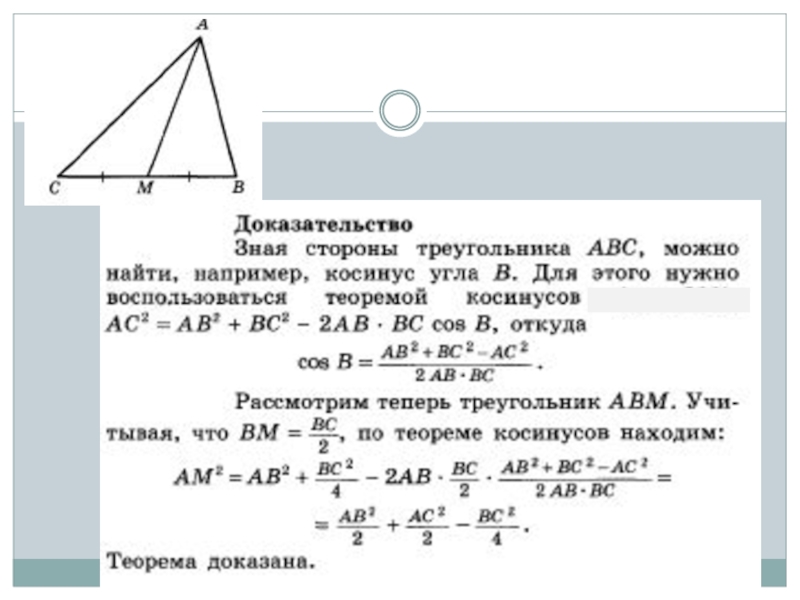
- 5. Длина медианы треугольника вычисляется по формуле:
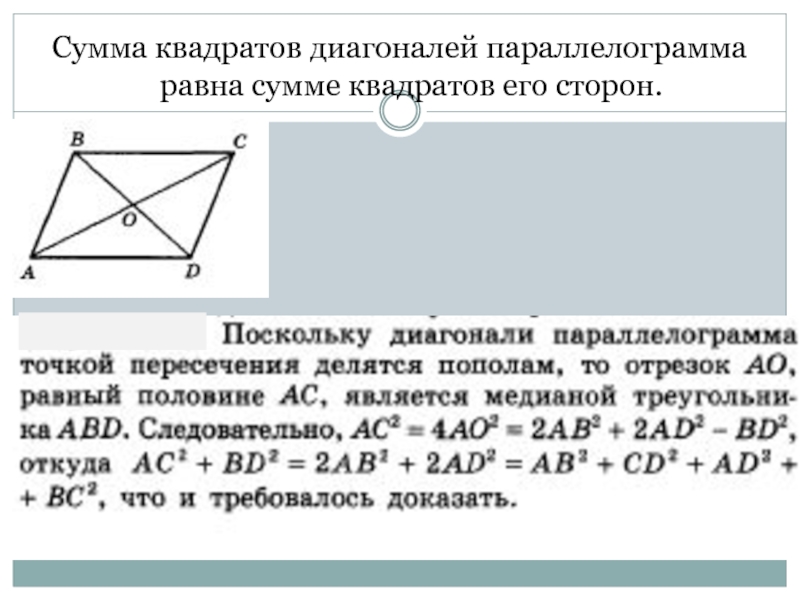
- 7. Сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон.
- 8. Следствие. Длины медиан и длины сторон треугольника связаны формулой
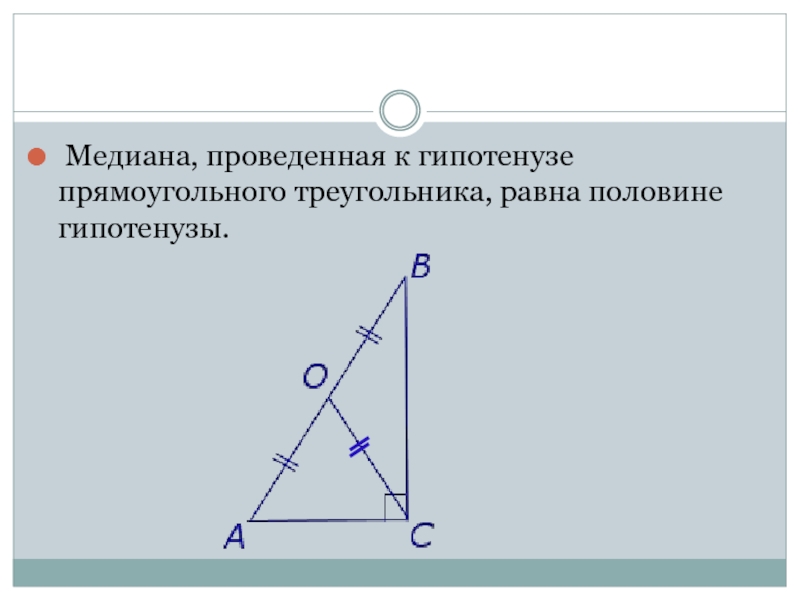
- 9. Медиана, проведенная к гипотенузе прямоугольного треугольника, равна половине гипотенузы.
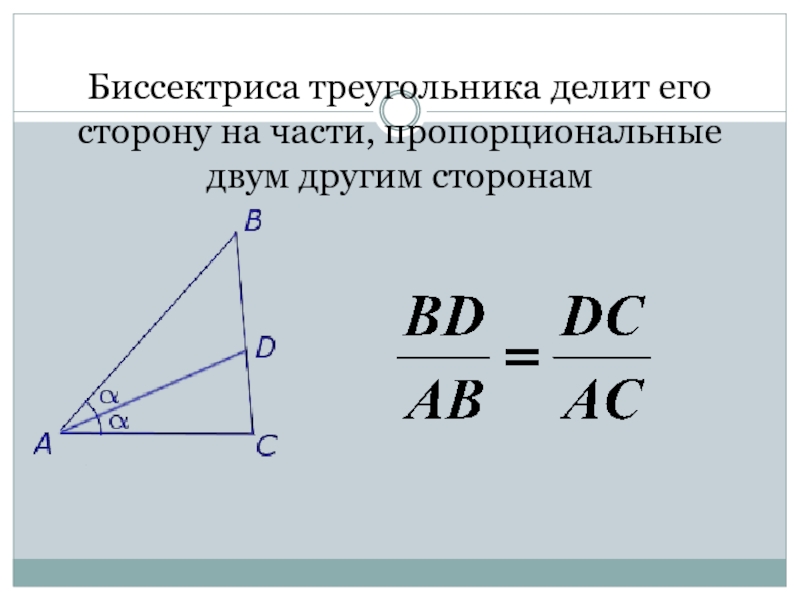
- 10. Биссектриса треугольника делит его сторону на части, пропорциональные двум другим сторонам
- 11. Для длины биссектрисы справедлива формула:
- 12. Точка пересечения биссектрис О делит биссектрису СD (теорема Ван-Обеля)
Что такое медиана треугольника? Медиана треугольника- это отрезок, соединяющий вершину треугольника с серединой противоположной стороны.
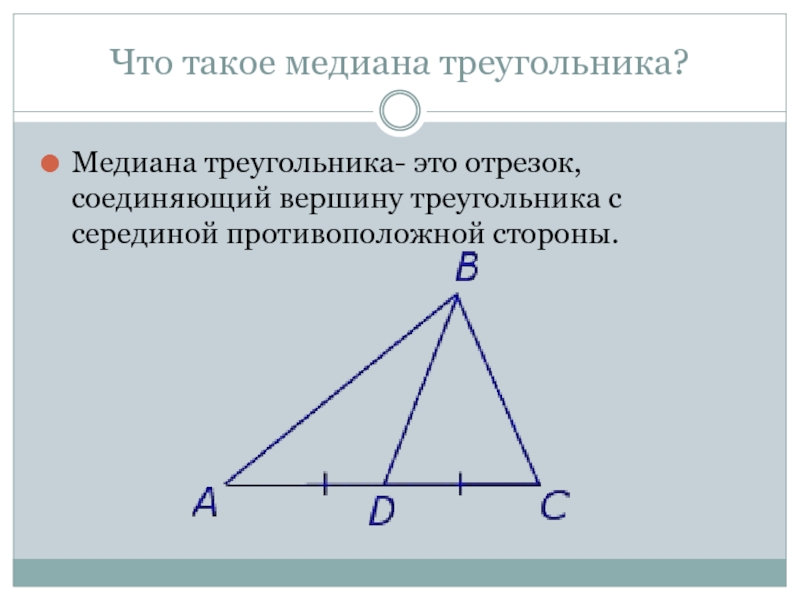
Слайд 2Что такое медиана треугольника?
Медиана треугольника- это отрезок, соединяющий вершину треугольника с
серединой противоположной стороны.
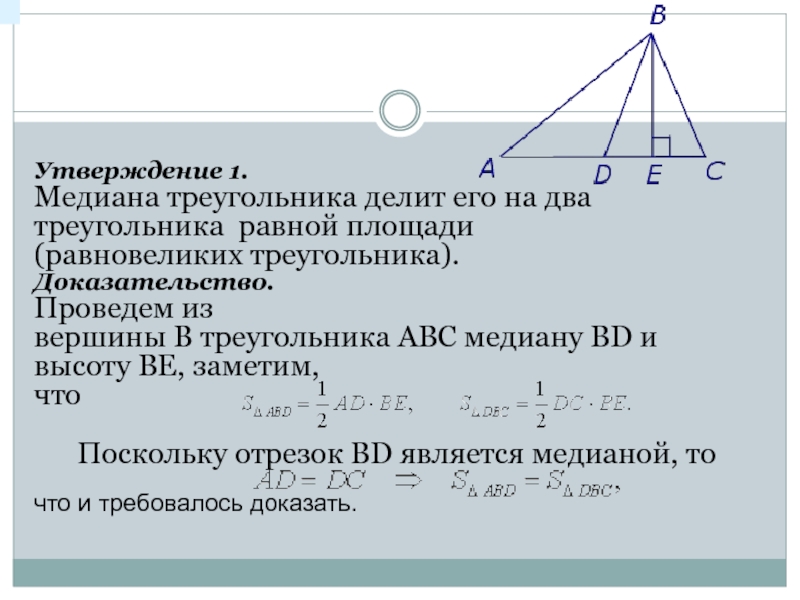
Слайд 3
Утверждение 1.
Медиана треугольника делит его на два треугольника равной площади
(равновеликих треугольника).
Доказательство.
Проведем из вершины B треугольника ABC медиану BD и высоту BE, заметим,
что
Поскольку отрезок BD является медианой, то
что и требовалось доказать.
Доказательство.
Проведем из вершины B треугольника ABC медиану BD и высоту BE, заметим,
что
Поскольку отрезок BD является медианой, то
что и требовалось доказать.
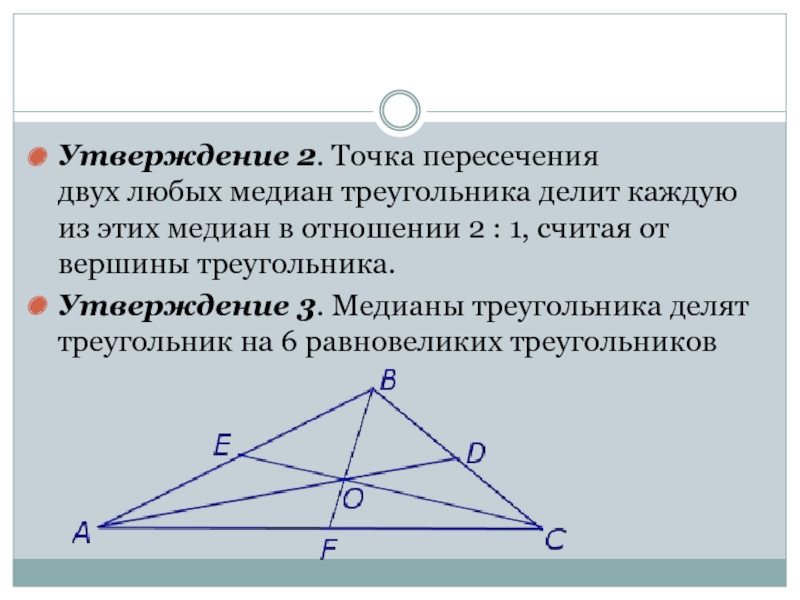
Слайд 4
Утверждение 2. Точка пересечения двух любых медиан треугольника делит каждую из этих
медиан в отношении 2 : 1, считая от вершины треугольника.
Утверждение 3. Медианы треугольника делят треугольник на 6 равновеликих треугольников
Утверждение 3. Медианы треугольника делят треугольник на 6 равновеликих треугольников
