- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
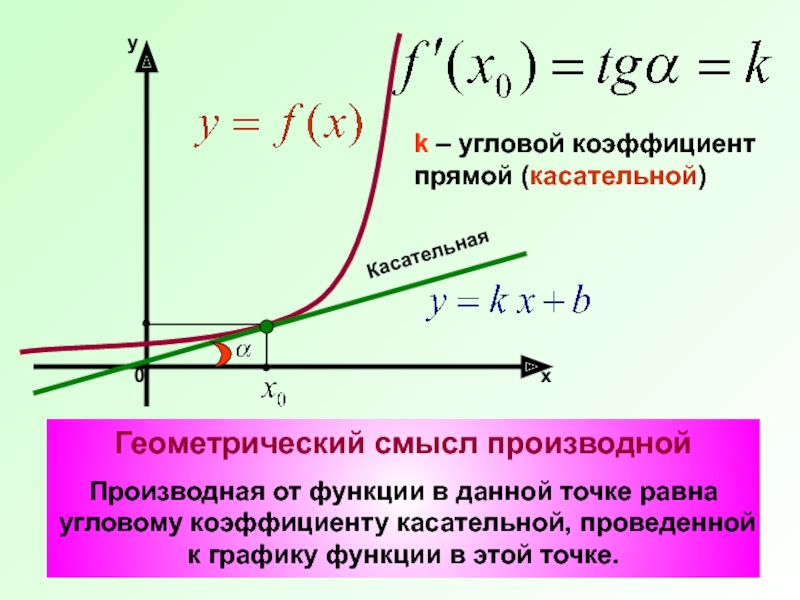
Геометрический смысл производной презентация
Содержание
- 1. Геометрический смысл производной
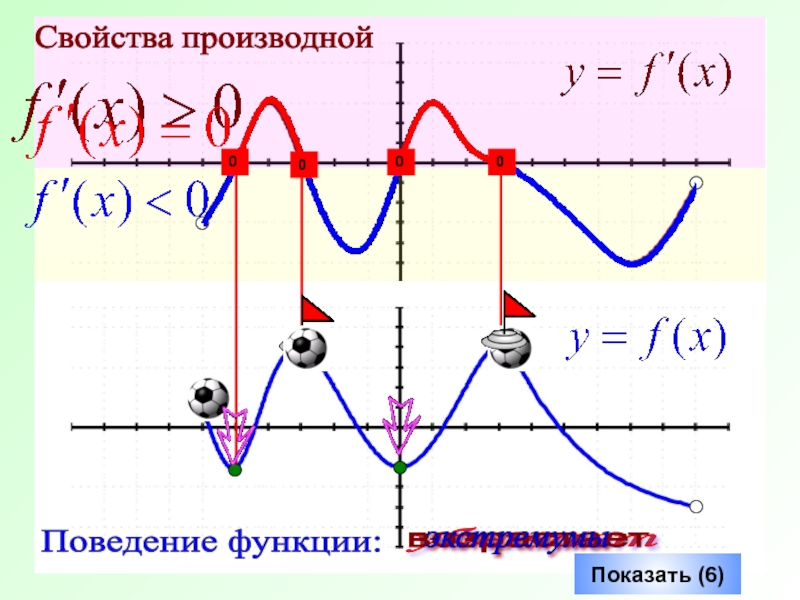
- 4. Показать (6) убывает возрастает экстремумы
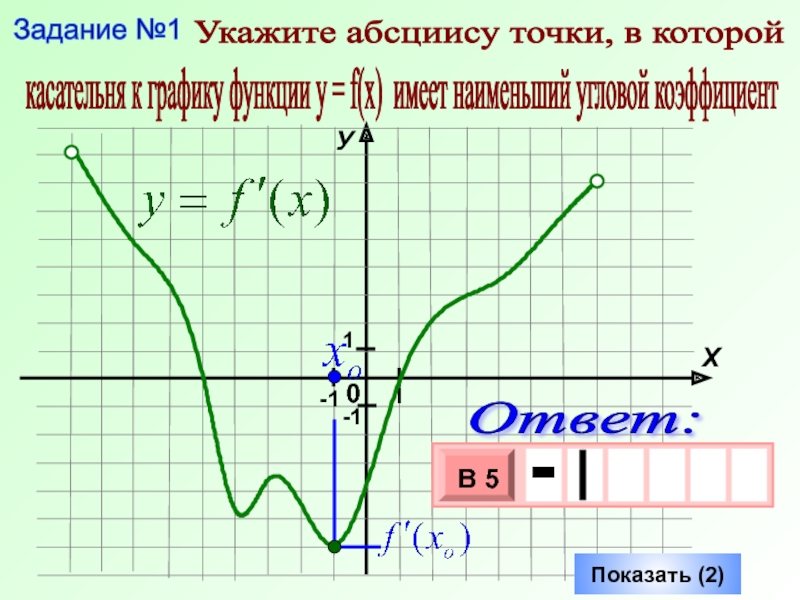
- 5. Показать (2) Задание №1 Укажите абсциису
- 6. Ищу наименьше значение производной Показать (2)
- 7. Показать (2) К графику функции у =
- 8. 2
- 9. Задание №3: Прямая, проходящая через начало
- 10. Задание №3: Прямая, проходящая через начало
- 11. Задание №4: К графику функции у
- 12. Задание №5: По графику производной функции
- 13. -4 -3
- 14. -4 -3 -2
- 15. Задание №8: По графику производной функции
- 16. Задание №9: Найдите значение производной функции в точке касания
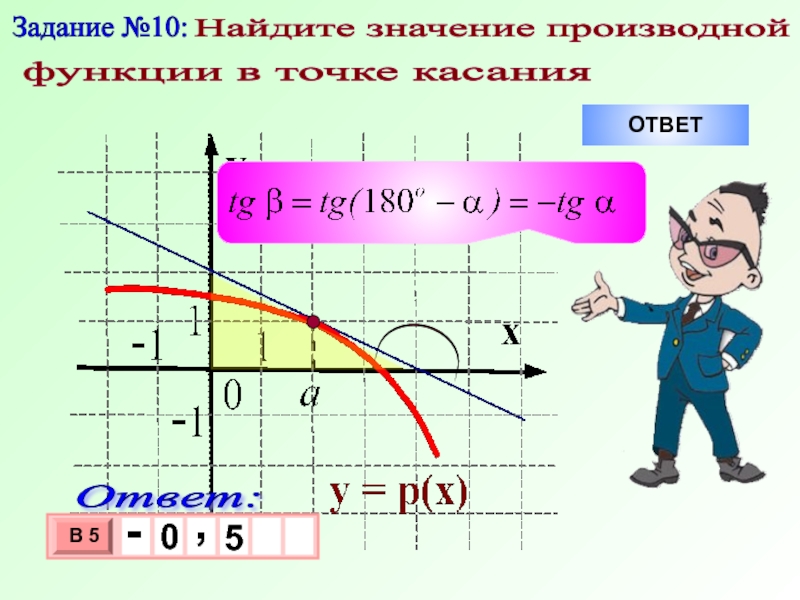
- 17. Задание №10: Найдите значение
- 18. Задание №11: Используя график производной
- 19. Задание №12: Используя график производной
- 20. Показать (2) Задание №13: По графику
- 21. Задание №14: По графику производной функции
- 22. Задание №15: По графику производной функции
- 23. Задание №16: Рассуждение (2) Ответ
- 24. Задание №17: По графику производной функции
- 25. Задание №18: По графику производной
- 26. Задание №19: По графику производной функции
- 27. 0 У Х 1 -1 1 -1
Слайд 5Показать (2)
Задание №1
Укажите абсциису точки, в которой
касательня к графику
Слайд 7Показать (2)
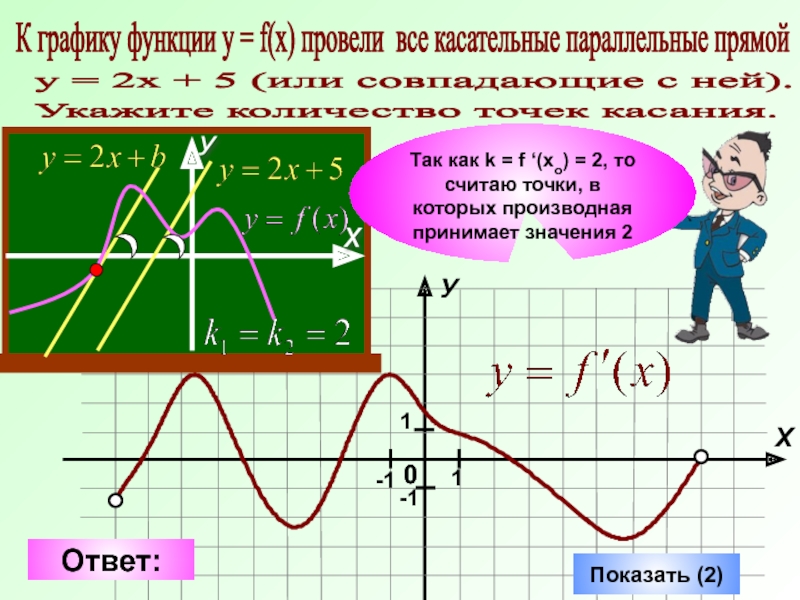
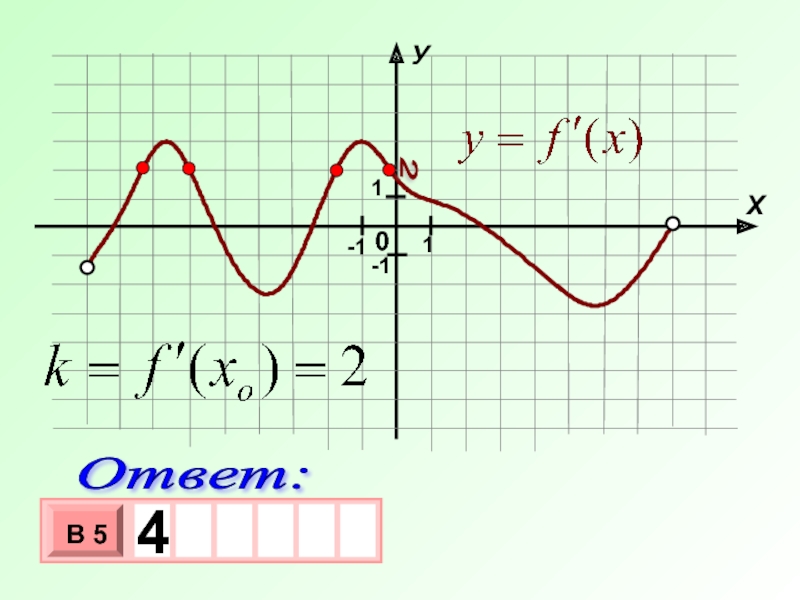
К графику функции у = f(x) провели все касательные параллельные
у = 2х + 5 (или совпадающие с ней).
Укажите количество точек касания.
Так как k = f ‘(xo) = 2, то считаю точки, в которых производная принимает значения 2
Ответ:
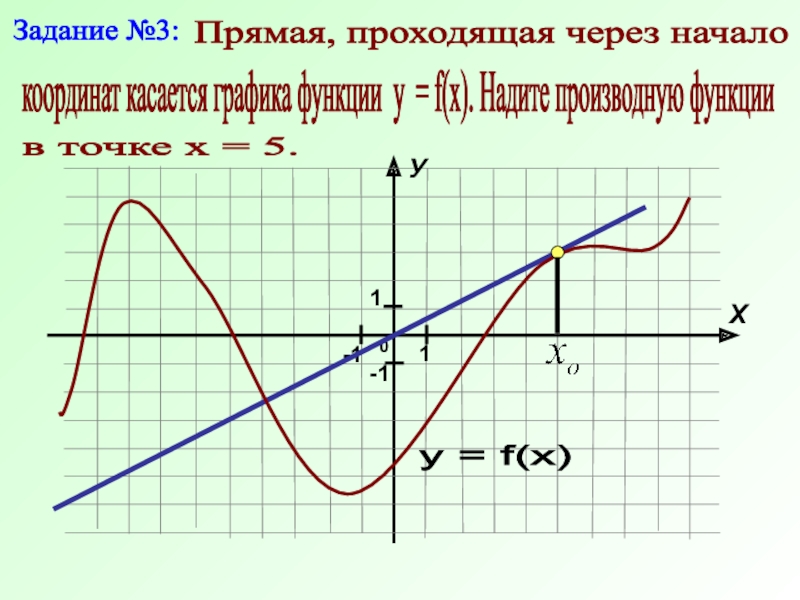
Слайд 9Задание №3:
Прямая, проходящая через начало
координат касается графика функции у
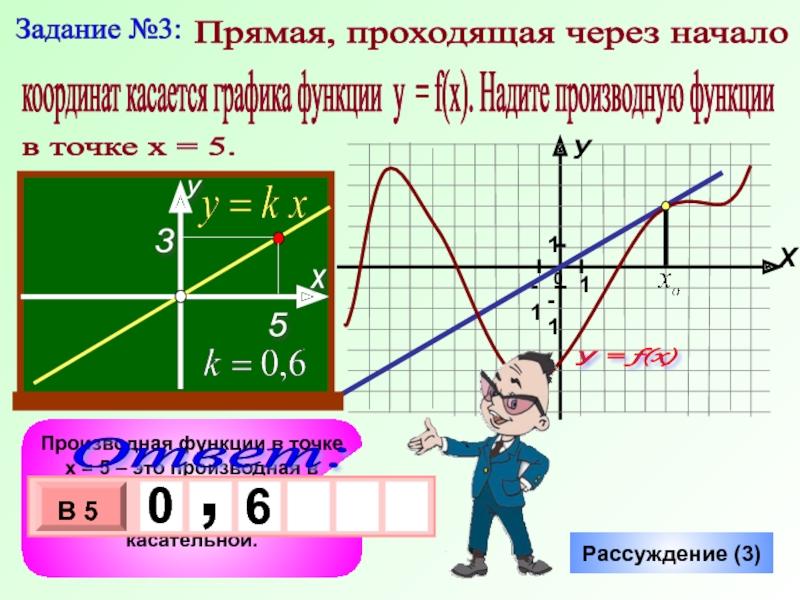
Слайд 10Задание №3:
Прямая, проходящая через начало
координат касается графика функции у
в точке х = 5.
Производная функции в точке х = 5 – это производная в точке касания хо, а она равна угловому коэффициенту касательной.
Рассуждение (3)
Слайд 11Задание №4:
К графику функции у = f(x) провели
касательные под
Рассуждение (2)
Ответ (2)
Слайд 12Задание №5:
По графику производной функции
указать наибольшую длину промежутка возрастания
Слайд 13
-4 -3 -2 -1
1 2
y = f /(x)
+ + +
- - -
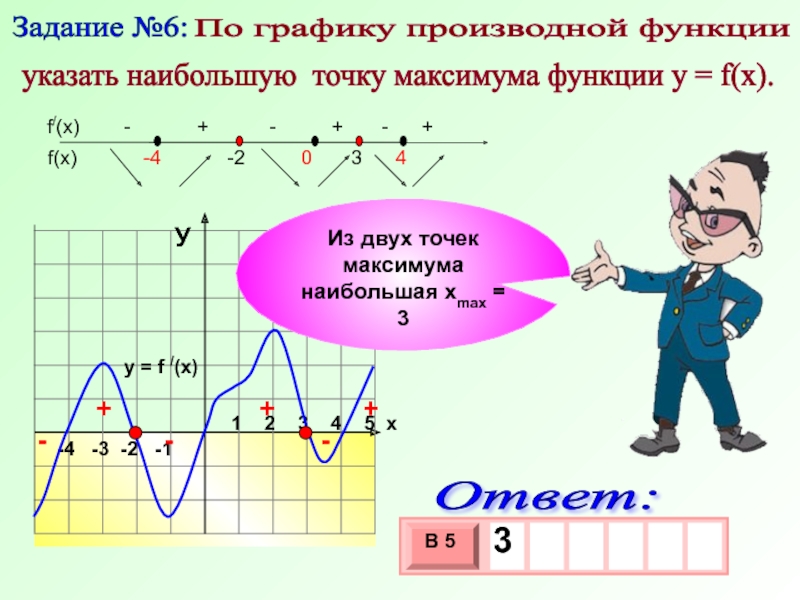
Из двух точек максимума наибольшая хmax = 3
Задание №6:
По графику производной функции
указать наибольшую точку максимума функции у = f(x).
У
Слайд 14 -4 -3 -2 -1
1 2
y = f /(x)
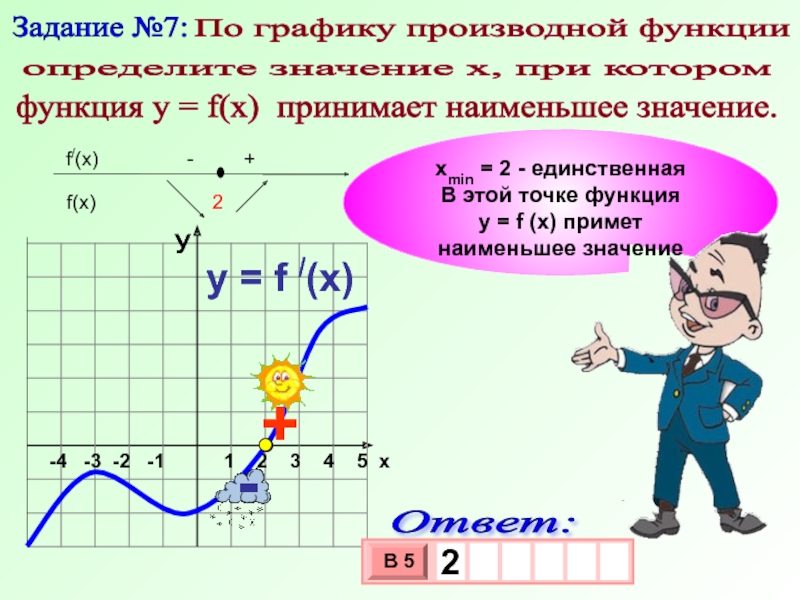
хmin = 2 - единственная
В этой точке функция у = f (x) примет наименьшее значение
У
Задание №7:
По графику производной функции
определите значение х, при котором
функция у = f(x) принимает наименьшее значение.
Слайд 15Задание №8:
По графику производной функции
указать количество точек максимума функции
Слайд 18Задание №11:
Используя график производной
функции, найдите значение функции у=f(x)
в
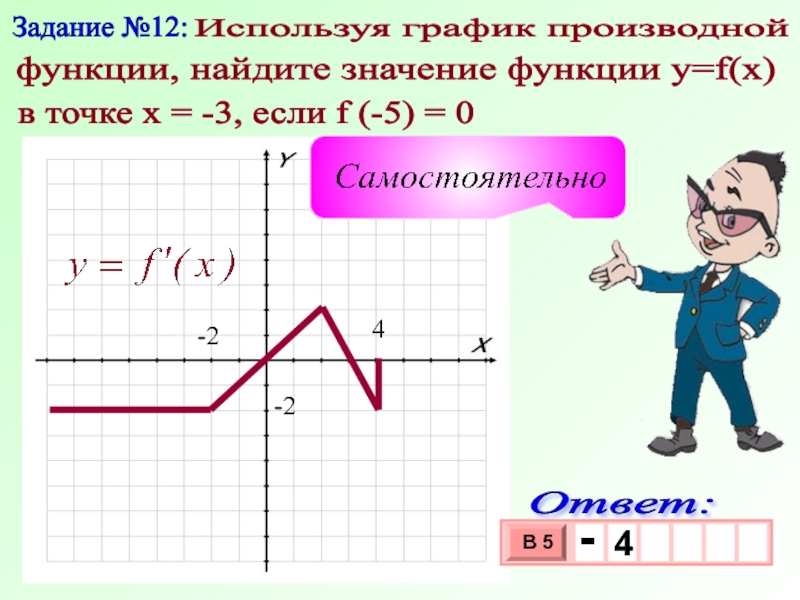
Слайд 19Задание №12:
Используя график производной
функции, найдите значение функции у=f(x)
в
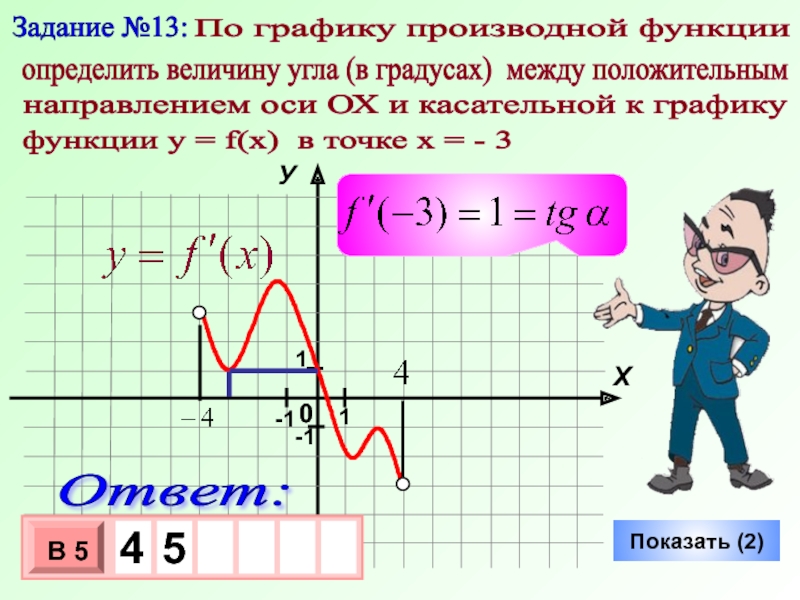
Слайд 20Показать (2)
Задание №13:
По графику производной функции
определить величину угла (в
функции у = f(x) в точке х = - 3
направлением оси ОХ и касательной к графику
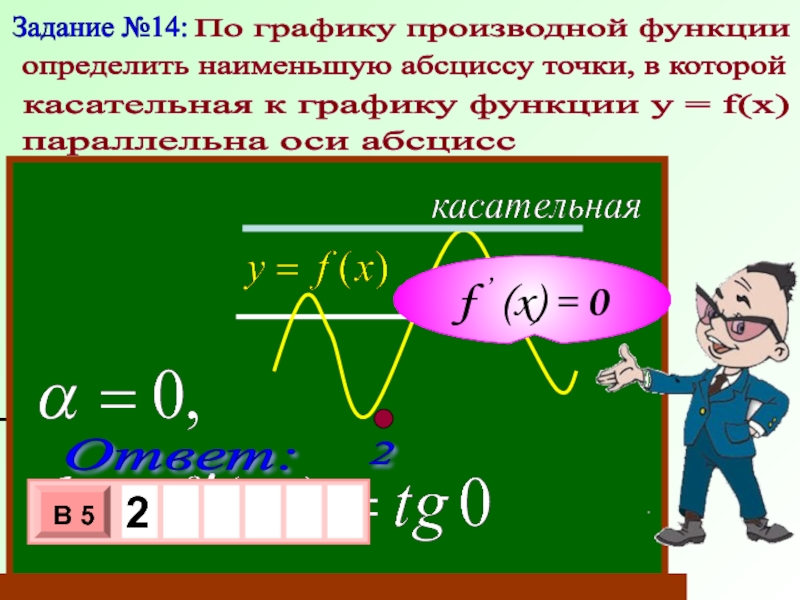
Слайд 21Задание №14:
По графику производной функции
определить наименьшую абсциссу точки, в
параллельна оси абсцисс
касательная к графику функции у = f(x)
f ’ (x) = 0
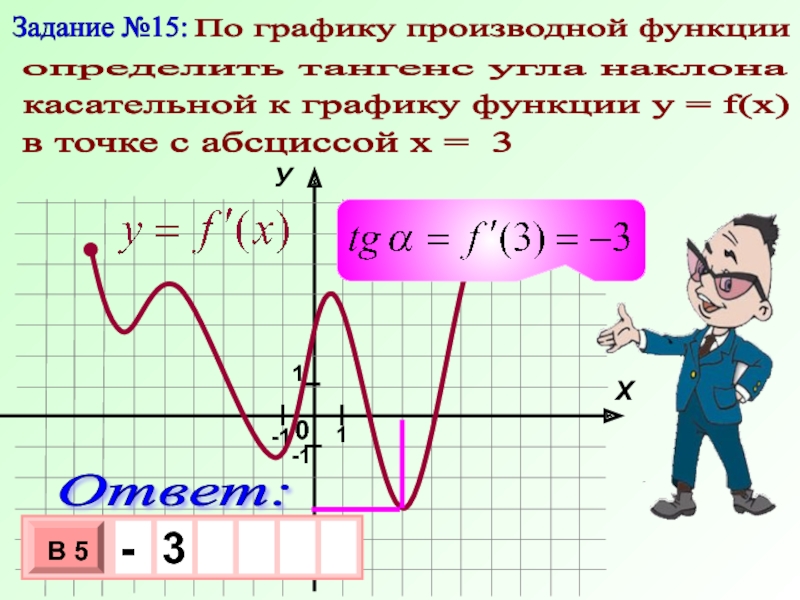
Слайд 22Задание №15:
По графику производной функции
определить тангенс угла наклона
в
касательной к графику функции у = f(x)
Слайд 23Задание №16:
Рассуждение (2)
Ответ
По графику производной функции
укажите количество касательных
у = f(x), расположенных под углом 60 градусов
к оси абсцисс
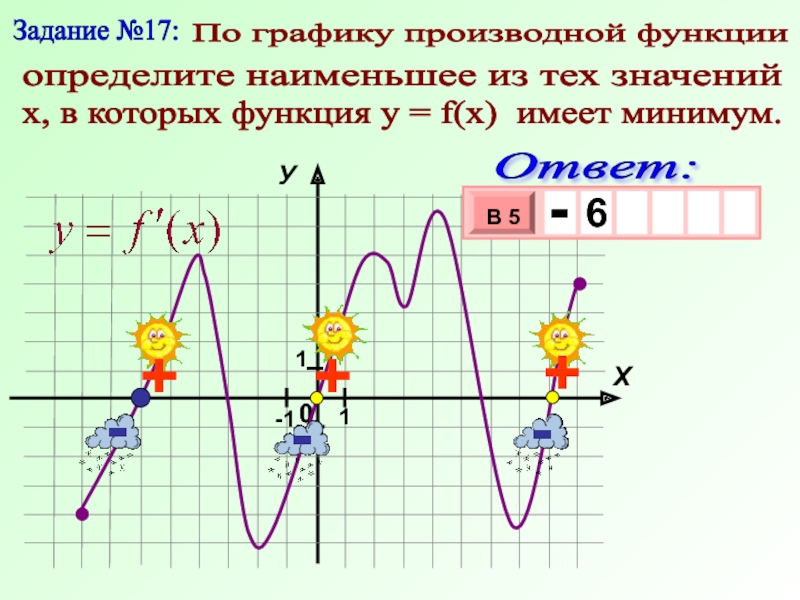
Слайд 24Задание №17:
По графику производной функции
определите наименьшее из тех значений
х, в которых функция у = f(x) имеет минимум.
Слайд 25
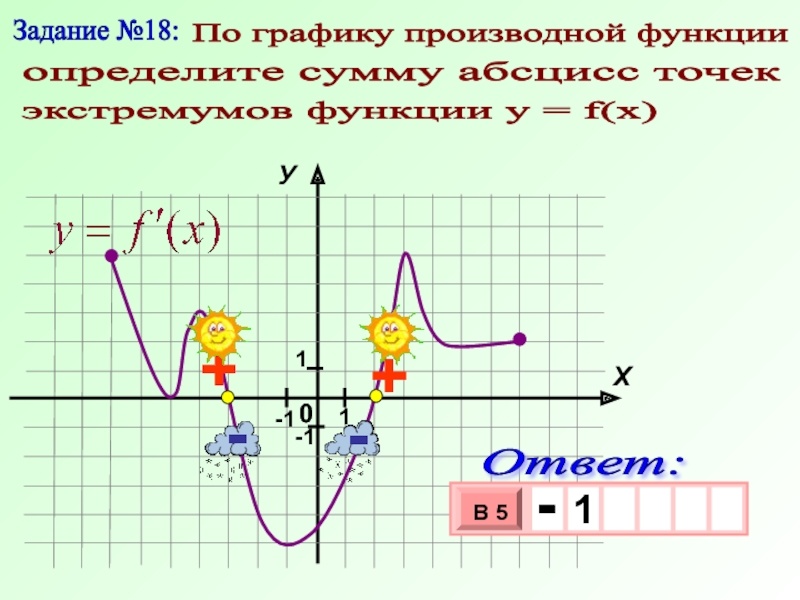
Задание №18:
По графику производной функции
определите сумму абсцисс точек
экстремумов
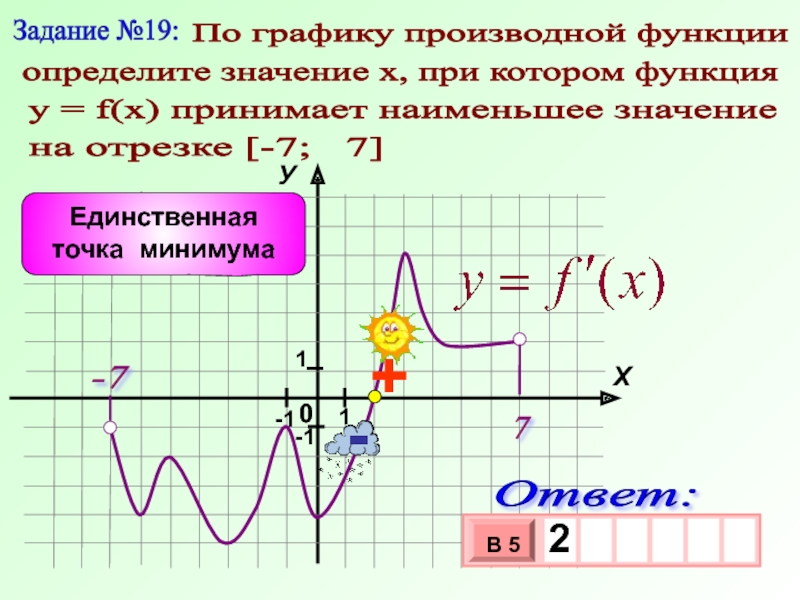
Слайд 26Задание №19:
По графику производной функции
определите значение х, при котором
у = f(x) принимает наименьшее значение
-7
7
на отрезке [-7; 7]
Единственная точка минимума
Слайд 270
У
Х
1
-1
1
-1
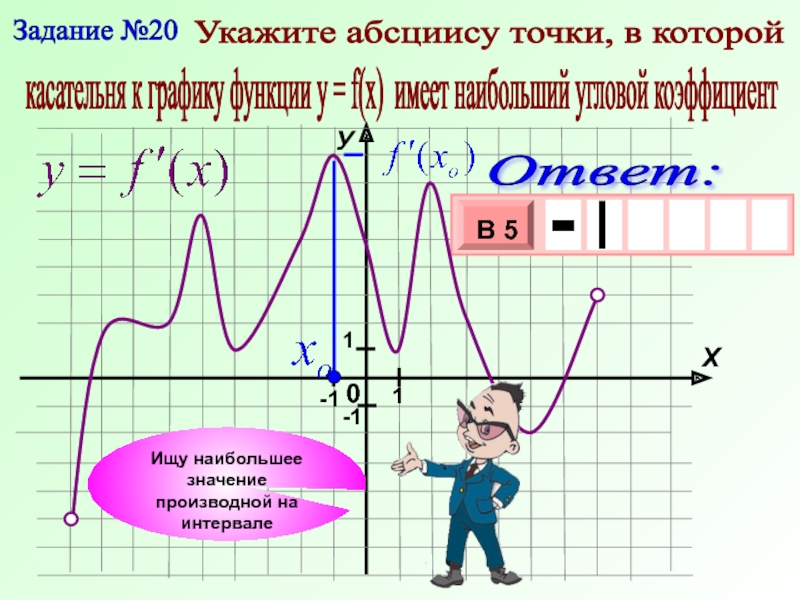
Задание №20
Укажите абсциису точки, в которой
касательня к графику функции