- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Прямоугольная система координат в пространстве презентация
Содержание
- 1. Прямоугольная система координат в пространстве
- 2. Вы уже знакомы с прямоугольной (Декартовой) системой
- 3. А, вот, прямоугольную систему координат в пространстве
- 4. Прямые с выбранными на них
- 5. Три плоскости, проходящие через
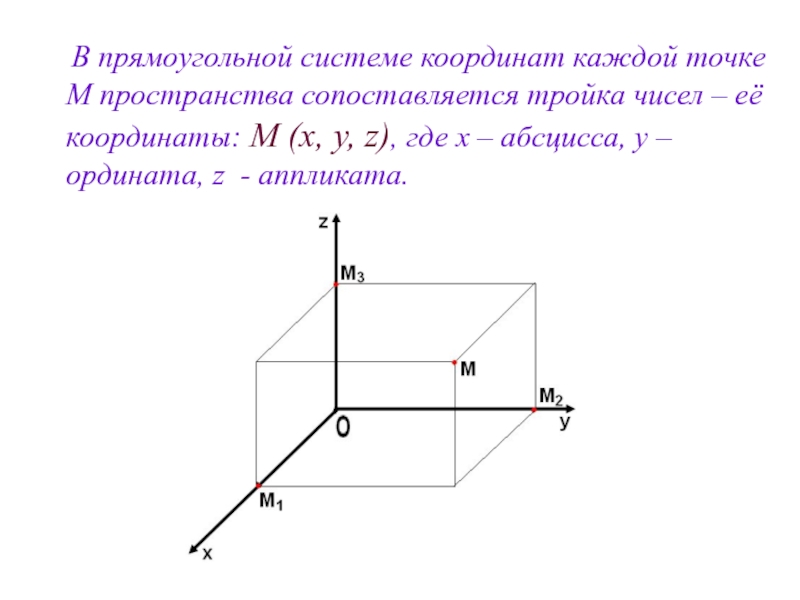
- 6. В прямоугольной системе координат каждой
- 7. Нахождение точки на координатной плоскости. Если, например,
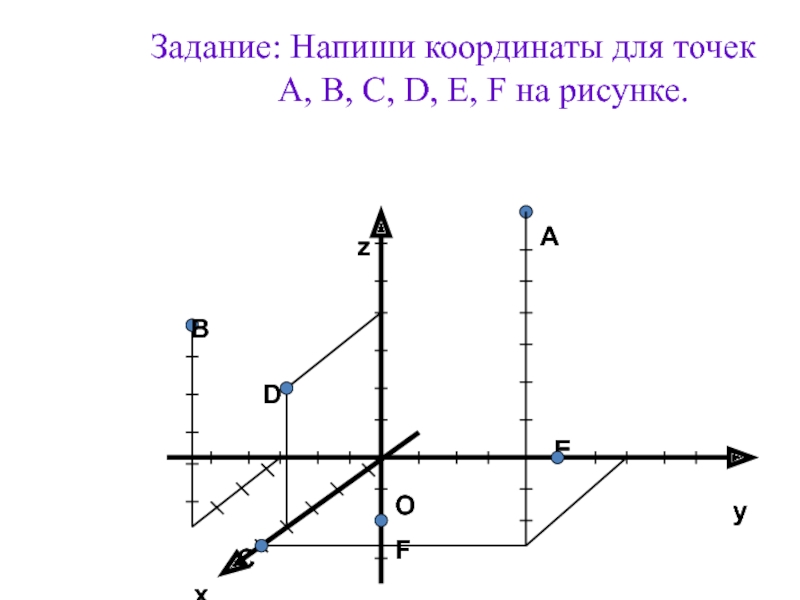
- 8. Задание: Напиши координаты для точек A,
- 9. Ответы A(5; 4; 10), B(4; -3; 6),
- 10. Оу (0,у,0)
- 11. Если М ОХУ, то
- 12. Координаты вектора в пространстве
- 13. Единичный вектор – вектор, длина которого равна
- 14. Любой вектор ā можно разложить по координатным
- 15. Запись координат вектора. Координаты вектора а будут
- 16. Формулы середины отрезка и расстояния между точками на плоскости.
- 17. Задача №1. Найдите координаты
- 18. I вариант Дано: А (3;-1), В (-2;4),
- 19. Расстояние между точками A(x1; y1;
- 20. Спасибо за урок!
Слайд 2Вы уже знакомы с прямоугольной (Декартовой) системой координат на плоскости, которую
в XIX в. ввёл
французский
математик
Рене Декарт
Слайд 3А, вот, прямоугольную систему координат в пространстве ввёл швейцарский,
немецкий,
российский
математик
Леонард Эйлер
в XVIIIв.
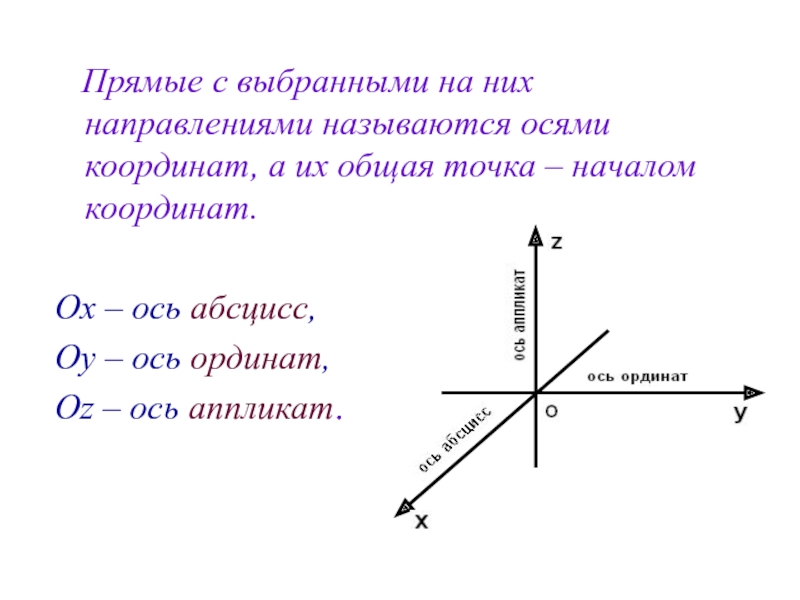
Слайд 4 Прямые с выбранными на них направлениями называются осями координат,
Ох – ось абсцисс,
Оу – ось ординат,
Оz – ось аппликат.
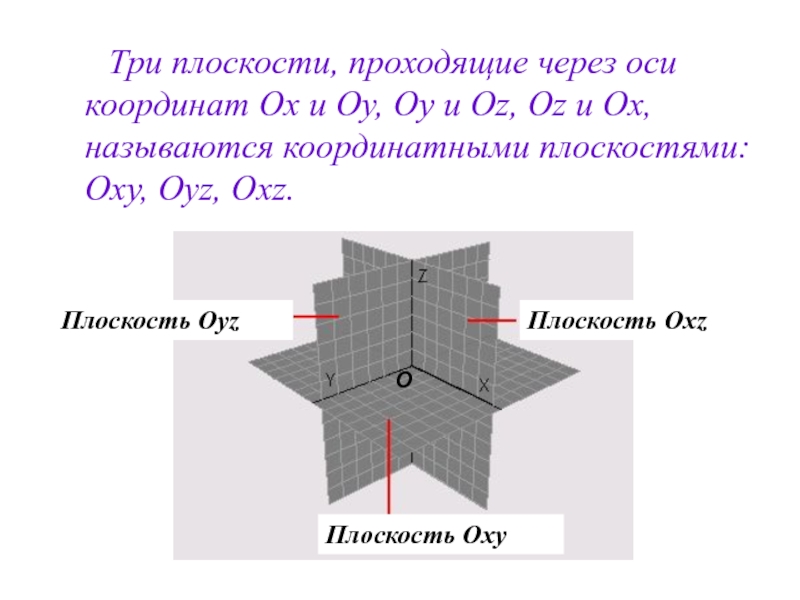
Слайд 5 Три плоскости, проходящие через оси координат Ох и
Плоскость Oxz
Плоскость Oxy
Плоскость Oyz
O
Слайд 6 В прямоугольной системе координат каждой точке М пространства сопоставляется
Слайд 7Нахождение точки на координатной плоскости.
Если, например, точка M лежит на координатной
Слайд 9Ответы
A(5; 4; 10),
B(4; -3; 6),
C(5; 0; 0),
D(4; 0; 4),
E(0; 5; 0),
F(0;
Сравни свои ответы.
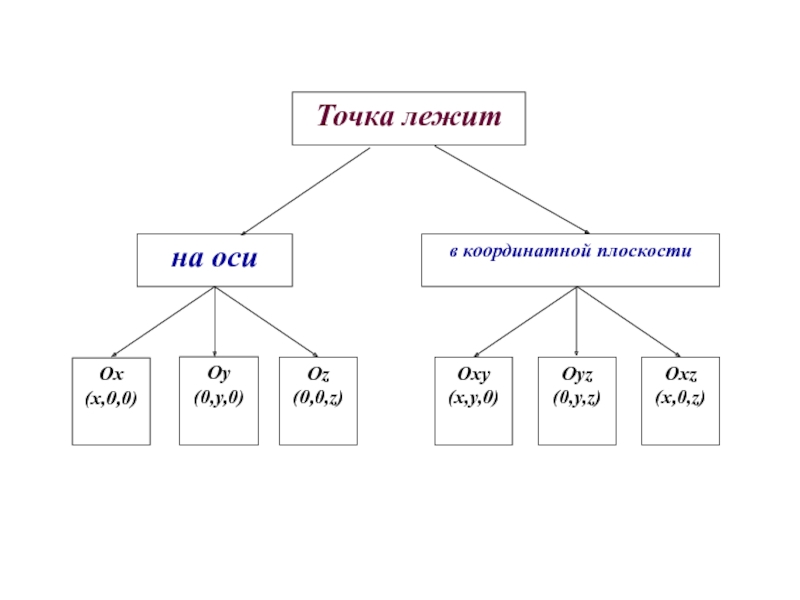
Слайд 11Если М ОХУ, то z=0
Если М
Если М OУZ, то X=0
Если М ОХ, то У=0 и Z=0
Если М OУ, то Х=0 и Z=0
Если М OZ, то Х=0 и У=0
Нахождение точки на координатной плоскости.
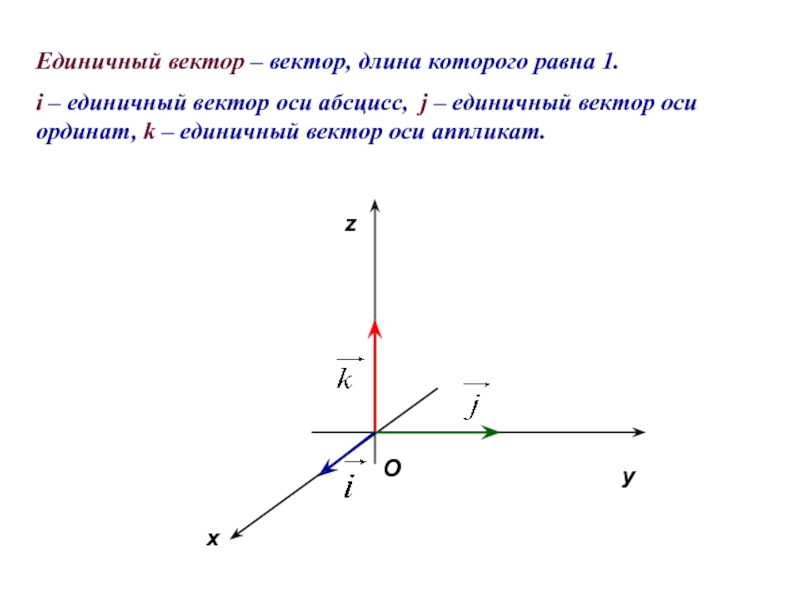
Слайд 13Единичный вектор – вектор, длина которого равна 1.
i – единичный вектор
x
z
y
O
Слайд 14Любой вектор ā можно разложить по координатным векторам, т.е. представить в
Нулевой вектор можно представить в виде:
Координаты равных векторов соответственно равны, т.е., если
ā { x1; y1; z1 } = b { x2; y2; z2 }, то
x1 = x2, y1 = y2, z1 = z2.
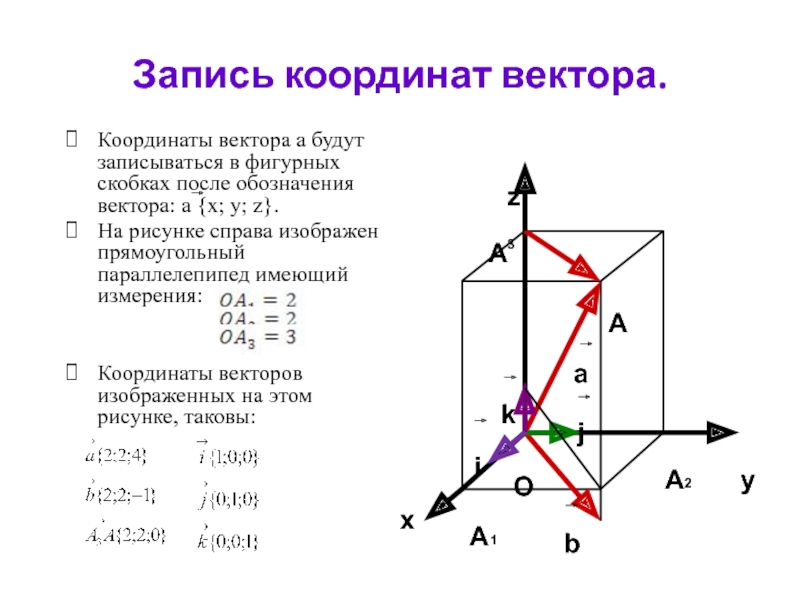
Слайд 15Запись координат вектора.
Координаты вектора а будут записываться в фигурных скобках после
На рисунке справа изображен прямоугольный параллелепипед имеющий измерения:
Координаты векторов изображенных на этом рисунке, таковы:
A
A
A
A
O
y
x
z
a
j
i
k
b
3
2
1
Слайд 17
Задача №1.
Найдите координаты середины отрезка АВ и длину отрезка АВ, если:
1
2 вариант А (3;4), В (2; -1)
Слайд 18I вариант
Дано: А (3;-1), В (-2;4),
точка М – середина АВ.
Найти: IАВI,
Решение:
Ответ:
II вариант
Дано: А (3;4), В (2;-1),
точка С – середина АВ.
Найти: IАВI, С(x;y).
Решение:
Ответ: