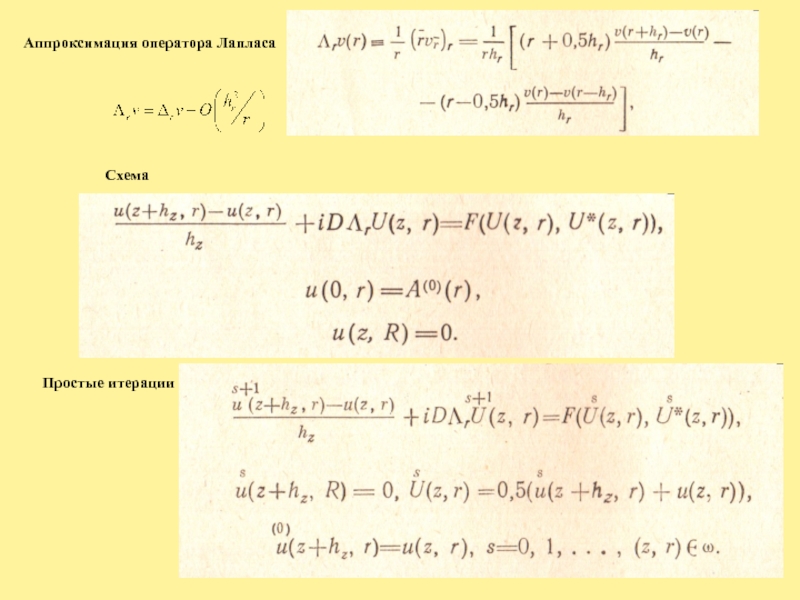1989.
2. Н.Бахвалов, Н.Жидков, Г.Кобельков. Численные методы. М., Физматлит, 2001.
3. А.А.Самарский, А.В.Гулин. Численные методы математической физики. 2000.
4. Г. Агравал. Нелинейная волоконная оптика. 1996
5. Г.И. Марчук. Методы вычислений, 1977
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Математическое моделирование в нелинейной оптике презентация
Содержание
- 1. Математическое моделирование в нелинейной оптике
- 2. РАСПРОСТРАНЕНИЕ СВЕТОВОГО ПУЧКА В СРЕДЕ С КУБИЧНОЙ
- 3. Однофотонное и двухфотонное поглощение (стационарный случай)
- 4. Нестационарный случай двухфотонного резонанса
- 5. МАТЕМАТИЧЕСКАЯ ПОСТАНОВКА ЗАДАЧИ О РАСПРОСТРАНЕНИИ МОДУЛИРОВАННЫХ ЭЛЕКТРОМАГНИТНЫХ ВОЛН В НЕЛИНЕЙНЫХ СРЕДАХ
- 6. ИНТЕГРАЛЫ ДВИЖЕНИЯ Существуют при условиях , U – действительная функция 2N переменных, такая что
- 7. 1-ый интеграл Если
- 8. Умножаем уравнения скалярно на
- 9. Нелинейность керровского типа при аксиально-симметричном распространении Координаты
- 10. Аппроксимация оператора Лапласа Схема Простые итерации
- 11. При условии
РАСПРОСТРАНЕНИЕ СВЕТОВОГО ПУЧКА В СРЕДЕ С КУБИЧНОЙ НЕЛИНЕЙНОСТЬЮ УЧЕТ ТЕПЛОВОГО МЕХАНИЗМА ИЗМЕНЕНИЯ ПОКАЗАТЕЛЯ ПРЕЛОМЛЕНИЯ - нет диффузии тепла вдоль оси распространения
Слайд 1Ю.Н.Карамзин, А.П.Сухоруков, В.А.Трофимов. Математическое моделирование в нелинейной оптике. М., Изд-во МГУ,
Слайд 2РАСПРОСТРАНЕНИЕ СВЕТОВОГО ПУЧКА В СРЕДЕ С КУБИЧНОЙ НЕЛИНЕЙНОСТЬЮ
УЧЕТ ТЕПЛОВОГО МЕХАНИЗМА
ИЗМЕНЕНИЯ ПОКАЗАТЕЛЯ ПРЕЛОМЛЕНИЯ
- нет диффузии тепла вдоль оси распространения
Слайд 5МАТЕМАТИЧЕСКАЯ ПОСТАНОВКА ЗАДАЧИ
О РАСПРОСТРАНЕНИИ МОДУЛИРОВАННЫХ
ЭЛЕКТРОМАГНИТНЫХ ВОЛН В НЕЛИНЕЙНЫХ СРЕДАХ
Слайд 6ИНТЕГРАЛЫ ДВИЖЕНИЯ
Существуют при условиях
, U – действительная функция 2N переменных, такая
что
Слайд 7
1-ый интеграл
Если выполняется условие 1), то умножаем уравнения скалярно на
и складываем
2-ой и 3-ий интегралы
Пусть выполняется 2), тогда сначала используем формулы интегрирования по частям
Слайд 8Умножаем уравнения скалярно на
и складываем
Для получаем 2-ой интеграл,
для - 3-ий интеграл.
Для получаем 2-ой интеграл,
для - 3-ий интеграл.
Для среды с кубичной нелинейностью
Трехчастотное взаимодействие
Соотношения Мэнли-Роу
Слайд 9Нелинейность керровского типа при аксиально-симметричном распространении
Координаты (r,z)
Стационарное взаимодействие произвольного числа электромагнитных
волн в нелинейной среде, когда отсутствует двулучепреломление, можно пренебречь эффектами дисперсионного расплывания импульсов и групповые скорости всех волн одинаковы
Схема строится на равномерной сетке со сдвигом по поперечной координате
Слайд 11При условии
итерации сходятся со скоростью геометрической
прогрессии со знаменателем . q связано с условием на правую
часть:
прогрессии со знаменателем . q связано с условием на правую
часть:
Схема консервативна, т.е. сохраняет разностные аналоги 1-го – 3-го интегралов
Скорость сходимости схемы в сеточной норме, связанной со скалярным
произведением при
+1
