- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Понятие функции презентация
Содержание
- 1. Понятие функции
- 2. ПРЕДЕЛ ФУНКЦИИ В ТОЧКЕ Лекция 3
- 3. Определение (по Коши): Запись: можно указать
- 4. Определение (по Гейне): числовая последовательность Число
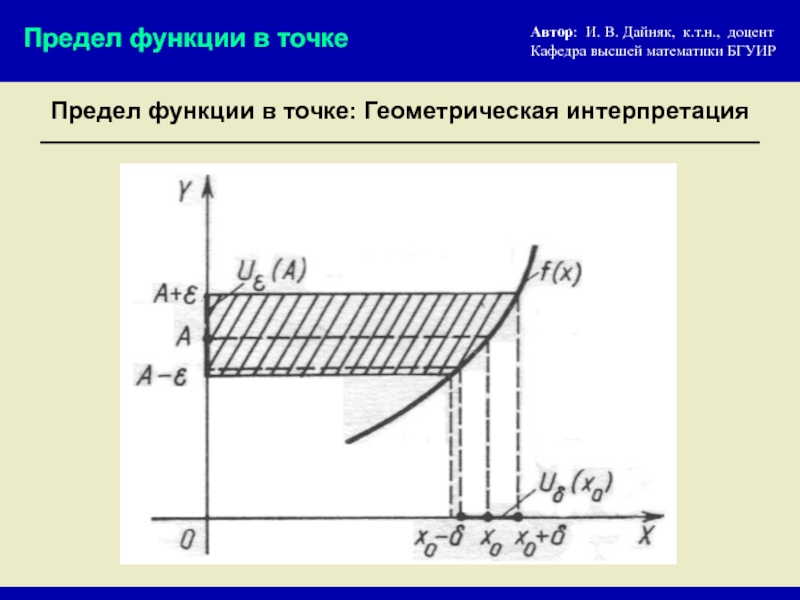
- 5. Предел функции в точке: Геометрическая интерпретация
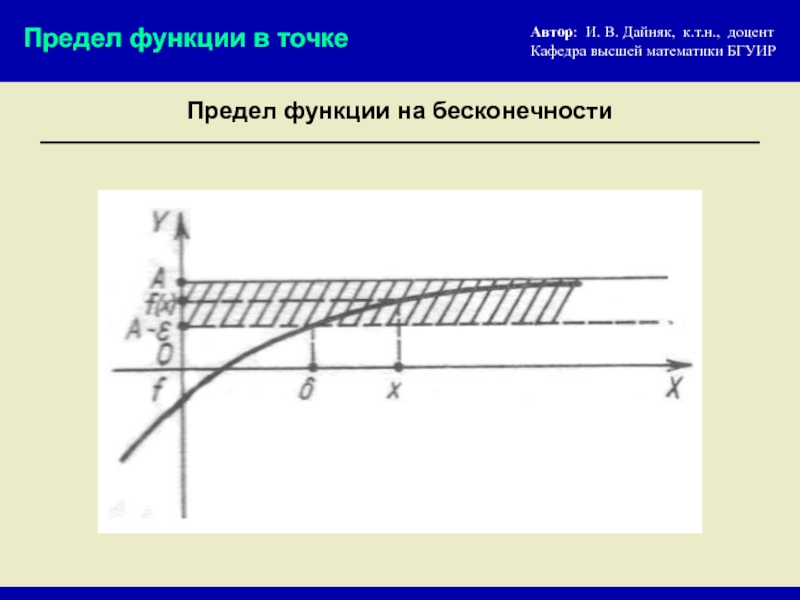
- 6. Предел функции на бесконечности Предел
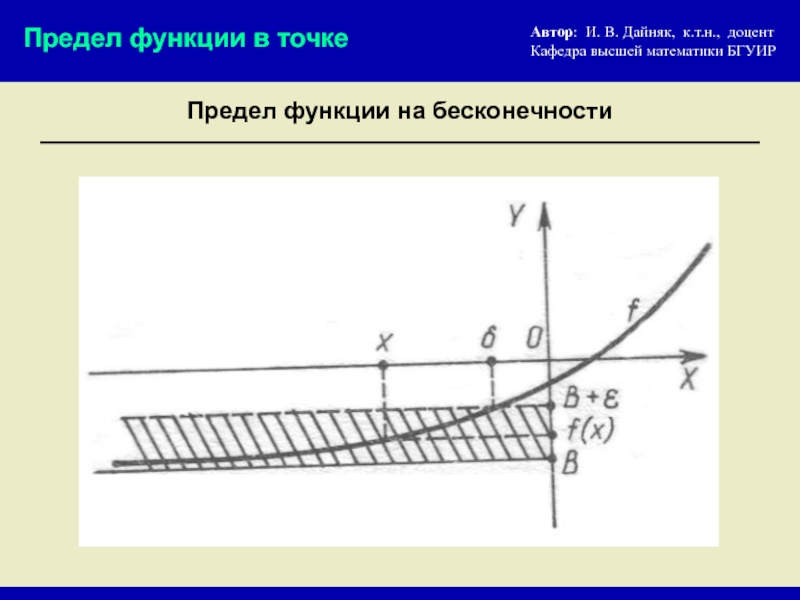
- 7. Предел функции на бесконечности Предел
- 8. Определения: Односторонний предел функции в
- 9. Определение: Односторонний предел функции в
- 10. Определение: последовательность Число А называется пределом
- 11. Замечание: При нахождении предела функции f
- 12. Свойства функций, имеющих предел в
- 13. Свойства функций, имеющих предел в
- 14. Свойства функций, имеющих предел в
- 15. Высшая математика math.mmts-it.org Автор:
ПРЕДЕЛ ФУНКЦИИ В ТОЧКЕ Лекция 3 Введение в математический анализ Автор: И. В. Дайняк, к.т.н., доцент
Кафедра высшей математики БГУИР
Слайд 1ПОНЯТИЕ ФУНКЦИИ
Лекция 3
Введение в математический анализ
Автор: И. В. Дайняк, к.т.н., доцент
Кафедра
высшей математики БГУИР
Слайд 2ПРЕДЕЛ ФУНКЦИИ В ТОЧКЕ
Лекция 3
Введение в математический анализ
Автор: И. В. Дайняк,
к.т.н., доцент
Кафедра высшей математики БГУИР
Слайд 3
Определение (по Коши):
Запись:
можно указать такое число
Число А называется пределом функции f
(x) в точке x0, если она определена в некоторой проколотой окрестности этой точки и если для любого сколь угодно малого
или
Предел функции в точке
Предел функции в точке
для которых
что для всех
выполнено неравенство
при
Автор: И. В. Дайняк, к.т.н., доцент
Кафедра высшей математики БГУИР
Слайд 4
Определение (по Гейне):
числовая последовательность
Число А называется пределом функции f (x) в
точке x0, если она определена в некоторой проколотой окрестности этой точки и если для любой числовой последовательности
Предел функции в точке
Предел функции в точке
значений функции
сходится к числу А при
сходящейся к х0, соответствующая
Определения предела по Коши и по Гейне эквивалентны.
Автор: И. В. Дайняк, к.т.н., доцент
Кафедра высшей математики БГУИР
Слайд 5
Предел функции в точке: Геометрическая интерпретация
Предел функции в точке
Автор: И. В.
Дайняк, к.т.н., доцент
Кафедра высшей математики БГУИР
Слайд 6
Предел функции на бесконечности
Предел функции в точке
Автор: И. В. Дайняк, к.т.н.,
доцент
Кафедра высшей математики БГУИР
Слайд 7
Предел функции на бесконечности
Предел функции в точке
Автор: И. В. Дайняк, к.т.н.,
доцент
Кафедра высшей математики БГУИР
Слайд 8
Определения:
Односторонний предел функции в точке
Предел функции в точке
Левая полуокрестность точки х0
– это произвольный интервал (а, х0), где а < х0.
Правая полуокрестность точки х0 – это произвольный интервал (х0, b), где х0 < b.
Автор: И. В. Дайняк, к.т.н., доцент
Кафедра высшей математики БГУИР
Слайд 9
Определение:
Односторонний предел функции в точке
Предел функции в точке
Запись:
последовательность
Число А называется пределом
функции f (x) в точке x0 слева, если она определена в левой полуокрестности этой точки и если для любой числовой последовательности
к числу А при
сходящейся к х0, соответствующая числовая
значений функции сходится
Автор: И. В. Дайняк, к.т.н., доцент
Кафедра высшей математики БГУИР
Слайд 10
Определение:
последовательность
Число А называется пределом функции f (x) в точке x0 справа,
если она определена в правой полуокрестности этой точки и если для любой числовой последовательности
Односторонний предел функции в точке
Предел функции в точке
к числу А при
сходящейся к х0, соответствующая числовая
Запись:
значений функции сходится
Автор: И. В. Дайняк, к.т.н., доцент
Кафедра высшей математики БГУИР
Слайд 11
Замечание:
При нахождении предела функции f (x) в точке x0 сама точка
х0 из рассмотрения исключается, а функция f (х) считается определённой в некоторой достаточно малой окрестности этой точки.
Предел функции в точке
Предел функции в точке
Автор: И. В. Дайняк, к.т.н., доцент
Кафедра высшей математики БГУИР
Слайд 12
Свойства функций, имеющих предел в точке
Предел функции в точке
1. Единственность предела
2.
Ограниченность функции
Если функция имеет предел в точке, то он единственный.
Функция, имеющая предел в точке, ограничена в некоторой проколотой окрестности этой точки.
3. Сохранение знака функции в окрестности предела
то существует проколотая
окрестность точки х0, в которой функция f (x) имеет знак, совпадающий со знаком числа А.
Если
Автор: И. В. Дайняк, к.т.н., доцент
Кафедра высшей математики БГУИР
Слайд 13
Свойства функций, имеющих предел в точке
Предел функции в точке
4. Предел «зажатой»
функции
и в некоторой проколотой окрестности точки х0 выполняется неравенство
то
Если
Автор: И. В. Дайняк, к.т.н., доцент
Кафедра высшей математики БГУИР
Слайд 14
Свойства функций, имеющих предел в точке
Предел функции в точке
5. Арифметические операции
над пределами
Если
то:
4)
1)
2)
3)
Автор: И. В. Дайняк, к.т.н., доцент
Кафедра высшей математики БГУИР
Слайд 15
Высшая математика
math.mmts-it.org
Автор: И. В. Дайняк, к.т.н., доцент
Кафедра высшей математики БГУИР
