- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Методы оптимальных решений. Симплексный метод презентация
Содержание
- 1. Методы оптимальных решений. Симплексный метод
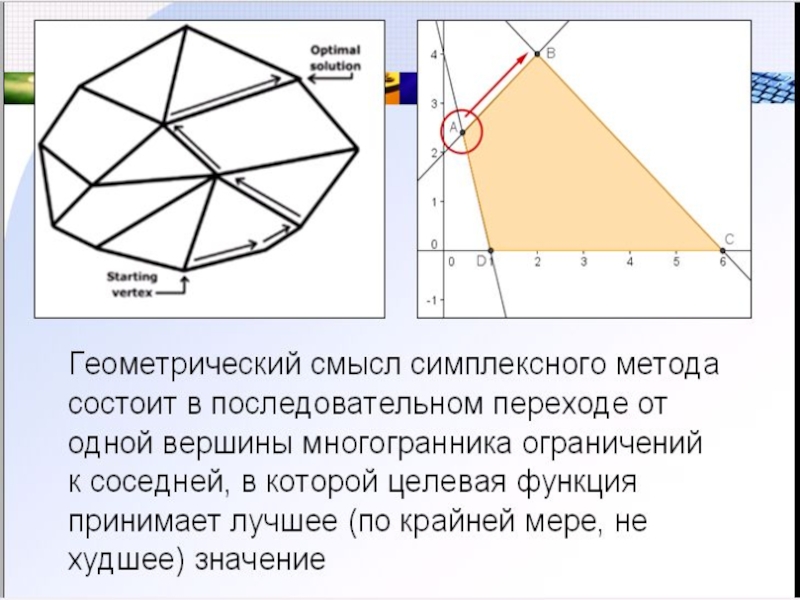
- 2. СИМПЛЕКСНЫЙ МЕТОД РЕШЕНИЯ ЗЛП Введение. Определение
- 7. Симплекс-метод Пусть требуется решить задачу
- 8. Симплекс-метод Так как решением задачи (2)
- 9. АЛГОРИТМ СИМПЛЕКС-МЕТОДА Определение К-матрицы в КЗЛП Рассмотрим
- 10. Переход от одной К-матрицы ЗЛП к другой
- 11. Переход от одной К-матрицы ЗЛП к другой
- 12. Переход от одной К-матрицы ЗЛП к другой
- 13. Переход от одной К-матрицы ЗЛП к другой
- 14. Переход от одной К-матрицы ЗЛП к другой
- 15. АЛГОРИТМ СИМПЛЕКС-МЕТОДА Возьмем в
- 16. Переход от одной К-матрицы ЗЛП к другой
- 17. Переход от одной К-матрицы ЗЛП к другой
- 18. Переход от одной К-матрицы ЗЛП к другой
- 19. Переход от одной К-матрицы ЗЛП к другой
- 20. Симплекс-разность К-матриц ЗЛП Симплекс-разность К-матриц ЗЛП. Изменение
- 21. Симплекс-разность К-матриц ЗЛП Пусть
- 22. Способ построения опорного плана Способ построения
- 23. Критерий оптимальности опорного плана Критерий оптимальности опорного
- 24. Критерий отсутствия конечного решения Критерий отсутствия конечного
- 25. Алгоритм симплекс-метода Алгоритм симплекс-метода Пусть известна исходная
- 26. Алгоритм симплекс-метода Шаг 1.
- 27. Алгоритм симплекс-метода Шаг 4. Вычисляем
- 28. ПРИМЕР №1 Пример 1 Симплекс-методом решить ЗЛП:
- 29. ПРИМЕР №1 Приводим систему линейных неравенств (2)
- 30. ПРИМЕР №1 Целевая функция (1) будет иметь
- 31. ПРИМЕР №1 Введём следующие обозначения:
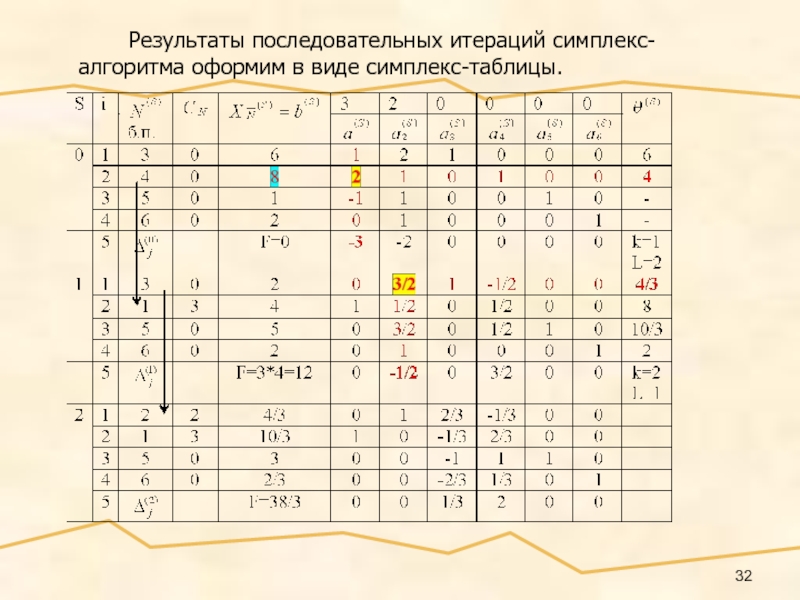
- 32. Результаты последовательных итераций симплекс-алгоритма оформим в виде симплекс-таблицы.
- 33. Пересчёт таблицы
- 34. ПРИМЕР №1 На второй итерации S=2, все
- 35. ПРИМЕР №2 Пример 2 Симплекс-методом решить ЗЛП:
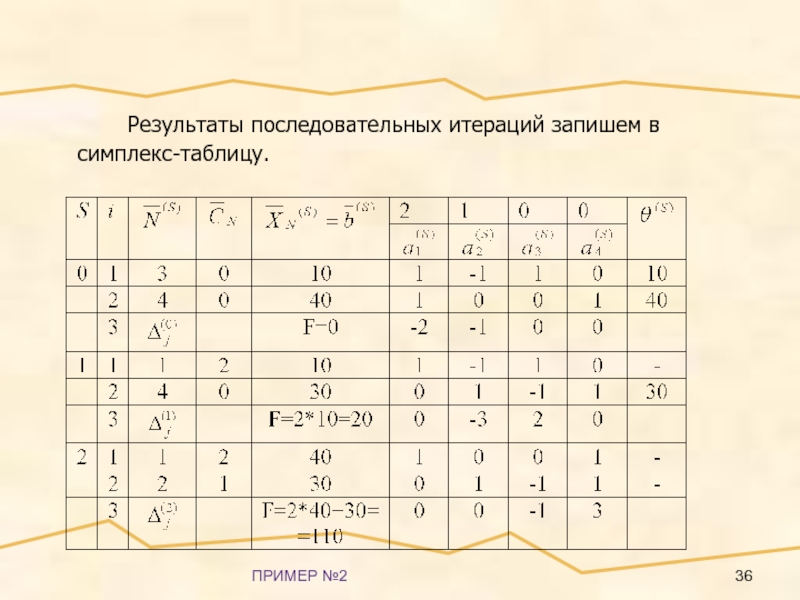
- 36. ПРИМЕР №2 Результаты последовательных итераций запишем в симплекс-таблицу.
- 37. ПРИМЕР №2 Из симплекс-таблицы при S=2 следует,
- 38. Список литературы Мастяева И.Н., Горемыкина Г.И., Семенихина
Слайд 1Дисциплина
МЕТОДЫ ОПТИМАЛЬНЫХ РЕШЕНИЙ
Кафедра математических методов в экономике
Факультет дистанционного обучения, направление 38.03.01
профиль «Финансы и кредит»
Слайд 2СИМПЛЕКСНЫЙ МЕТОД РЕШЕНИЯ ЗЛП
Введение.
Определение К-матрицы в КЗЛП
Переход от одной К-матрицы
Симплекс-разность К-матрицы КЗЛП
Способ построения опорного плана, более близкого к оптимальному
Критерий оптимальности опорного плана
Критерий отсутствия конечного решения
Алгоритм симплексного метода
Пример 1
Пример 2
Слайд 8Симплекс-метод
Так как решением задачи (2) является крайняя точка множества Р
1) обоснование способа перехода от одного опорного плана (К-матрицы) к другому;
2) указание признака оптимальности, позволяющего проверить, является ли данный опорный план оптимальным;
3) указание способа построения нового опорного плана, более близкого к оптимальному;
4) указание признака отсутствия конечного решения.
Слайд 9АЛГОРИТМ СИМПЛЕКС-МЕТОДА
Определение К-матрицы в КЗЛП
Рассмотрим каноническую задачу линейного программирования (КЗЛП):
Будем
(*)
где – j-й столбец матрицы А.
Дадим одно из определений опорного плана. ОП ЗЛП будем называть такой план , что векторы , входящие в разложение со строго положительными , линейно независимы.
К-матрицей КЗЛП будем называть расширенную матрицу системы линейных уравнений, равносильной системе (*), содержащую единичную подматрицу на месте первых n своих столбцов и все элементы (n+1)-го которой неотрицательны. Число К-матриц конечно и не превышает . Каждая К-матрица определяет ОП КЗЛП и наоборот.
Слайд 10Переход от одной К-матрицы ЗЛП к другой
Переход от одной К-матрицы
Пусть известна К-матрица
(3)
Обозначим через вектор номеров базисных (единичных) столбцов матрицы , - вектор, компоненты которого есть базисные компоненты опорного плана, определяемого матрицей , и могут быть отличны от нуля.
Слайд 11Переход от одной К-матрицы ЗЛП к другой
Остальные (n - m)
,
тогда ; и, следовательно, опорный план, определяемый , имеет вид:
Слайд 12Переход от одной К-матрицы ЗЛП к другой
Выберем в матрице столбец , не принадлежащий единичной подматрице, т. е. , , и такой, что в этом столбце есть хотя бы один элемент больше нуля.
Пусть . Считая направляющим элементом, совершим над матрицей один шаг метода Жордана - Гаусса. В результате получим новую матрицу
,
в которой стал единичным, но которая может и не быть К-матрицей, т.к. среди величин могут быть отрицательные.
Слайд 13Переход от одной К-матрицы ЗЛП к другой
Теорема 1.
Пусть в каком-либо столбце К-матрицы - есть хотя бы
один строго положительный элемент ( , ) . Тогда с помощью
одного шага метода Жордана-Гаусса можно построить новую К-матрицу
, выбрав направляющий элемент из условия
Слайд 14Переход от одной К-матрицы ЗЛП к другой
Доказательство:
Пусть известна К-матрица
задачи
,
,
следовательно,
Остальные n-m компонент опорного плана равны нулю.
Слайд 15АЛГОРИТМ СИМПЛЕКС-МЕТОДА
Возьмем в матрице
Пусть .
Считая направляющим элементом, совершим над матрицей один шаг метода Жордана-Гаусса.
В результате получим новую матрицу
,
элементы которой выражаются через элементы матрицы по следующим формулам:
Слайд 16Переход от одной К-матрицы ЗЛП к другой
(1*)
(2*)
(3*)
Таким образом, в результате
Гаусса мы получили L-матрицу ЗЛП, причем компоненты вектора
выражаются по следующим формулам:
(4*)
Слайд 17Переход от одной К-матрицы ЗЛП к другой
Однако матрица
Получим условия, которым должен удовлетворять направляющий элемент , чтобы
.
Из следует, что
тогда и только тогда, когда
(4)
Это первое условие, которое мы должны наложить на выбор
направляющего элемента.
Слайд 18Переход от одной К-матрицы ЗЛП к другой
Из
тогда и только тогда, когда
(5)
Условие (5) выполняется для всех ,
Перепишем неравенство (5) для строго положительных
в виде (6)
Слайд 19Переход от одной К-матрицы ЗЛП к другой
Очевидно, неравенство (6) будет
если выбрать таким, что
(7)
Если минимум в соотношении (7) достигается при одном значении
индекса i, то , т. е. матрица определяет в этом
случае план ЗЛП.
Если минимум в соотношении (7) достигается при нескольких значе-
ниях индекса i ,то
Тогда при
, т.е. матрица
определяет вырожденный опорный план ЗЛП.
(ч.т.д.)
Слайд 20Симплекс-разность К-матриц ЗЛП
Симплекс-разность К-матриц ЗЛП. Изменение функции
Определение.
Величину
,
где - вектор, компонентами которого являются коэффициенты
линейной функции при базисных ( ) переменных
опорного плана, определяемого матрицей , назовем j-й
симплекс - разностью матрицы .
Слайд 21Симплекс-разность К-матриц ЗЛП
Пусть и
и соответственно. Тогда очевидно, что
и
,
где К-номер столбца , вводимого в базис при получении
матрицы из .
Слайд 22Способ построения опорного плана
Способ построения опорного плана
Теорема 2.
Пусть в матрице есть , и в столбце
( , ) есть хотя бы один строго положительный элемент.
Тогда от матрицы можно перейти к матрице , причем
.
Слайд 23Критерий оптимальности опорного плана
Критерий оптимальности опорного плана
Теорема 3
Пусть все симплекс -
Слайд 24Критерий отсутствия конечного решения
Критерий отсутствия конечного решения.
Теорема 4
Пусть в матрице
Слайд 25Алгоритм симплекс-метода
Алгоритм симплекс-метода
Пусть известна исходная К-матрица ЗЛП,
Последовательно строятся К-матрицы
ЗЛП, пока не выполнится критерий оптимальности или критерий, позволяющий убедиться в отсутствии конечного решения.
Рассмотрим алгоритм S-ой итерации симплекс-метода. В начале S-ой итерации имеем К-матрицу ЗЛП, определяющую опорный план
Слайд 26Алгоритм симплекс-метода
Шаг 1.
Вычисляем для столбцов
Шаг 2.
Если , то опорный план является оптимальным, а есть оптимальное
значение линейной формы , иначе переходим к шагу 3
Шаг 3.
Если то ЗЛП не имеет конечного решения.
Иначе находим номер L из условия
;
направляющий элемент на S-ой итерации метода есть элемент
Слайд 27Алгоритм симплекс-метода
Шаг 4.
Вычисляем компоненты вектора
Шаг 5.
Производим один шаг метода Жордана-Гаусса с направляющим
элементом . Присваиваем переменной S алгоритма
значение S+1 и переходим к шагу 1.
Слайд 29ПРИМЕР №1
Приводим систему линейных неравенств (2) к каноническому виду, вводя в
, .
Получим систему линейных уравнений:
(3)
Слайд 30ПРИМЕР №1
Целевая функция (1) будет иметь вид
Расширенная матрица
системы
Слайд 31ПРИМЕР №1
Введём следующие обозначения:
S-номер итерации
i-номера строк таблицы
-номера
-коэффициенты целевой функции при столбцах, образующих единичную подматрицу
-соответствуют переменным задачи
-сначала содержит правые части системы уравнений , в конце алгоритма - искомые значения переменных
-для вычисления значений
Слайд 34ПРИМЕР №1
На второй итерации S=2, все
определяемый К-матрицей , оптимальный,
Оптимальное значение линейной формы равно:
Слайд 35ПРИМЕР №2
Пример 2
Симплекс-методом решить ЗЛП:
(4)
(5)
Приводим ЗЛП (4-5) к каноническому виду
(6)
Слайд 37ПРИМЕР №2
Из симплекс-таблицы при S=2 следует, что согласно шагу 3
симплекс-алгоритма,
т.к. отрицательная симплекс-разность соответствует
столбцу , все элементы которого неположительны.
Итак,
Слайд 38Список литературы
Мастяева И.Н., Горемыкина Г.И., Семенихина О.Н., Методы оптимизации: линейные модели.
Мастяева И.Н., Горемыкина Г.И., Семенихина О.Н., Исследование операций и методы оптимизации. М.: МЭСИ, 2015.
Мастяева И.Н., Горемыкина Г.И., Семенихина О.Н., Методы оптимальных решений. М.: Курс, 2016.