Дифференциальные уравнения презентация

Содержание

1. Дифференциальные уравнения
2. 21. 1. ПОНЯТИЕ ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ Дифференциальным
3. Если искомая функция зависит от одной переменной,
4. Простейшим примером ДУ является задача о нахождении
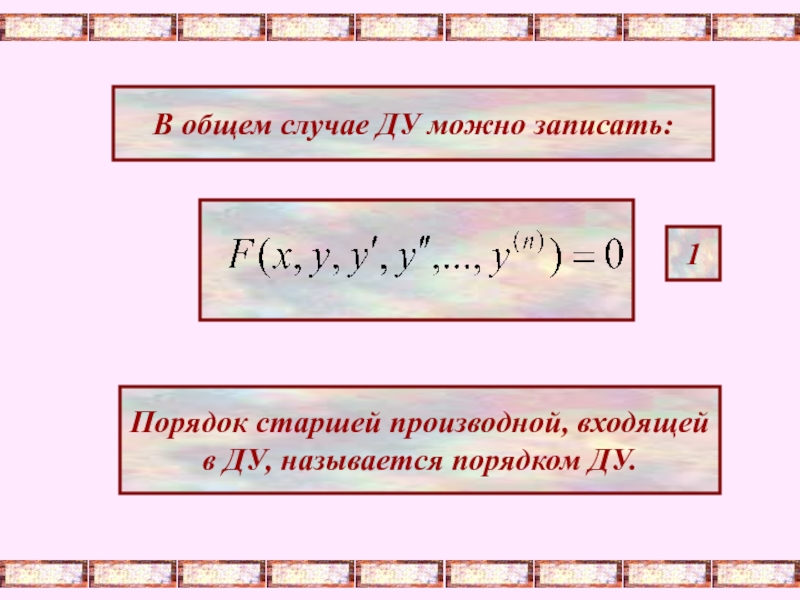
5. В общем случае ДУ можно записать:
6. Например, дифференциальное уравнение является уравнением третьего порядка.
7. Например, решением дифференциального уравнения является функция поскольку Подставляем в уравнение:
8. ПРИМЕР. Решить дифференциальное уравнение:
9. РЕШЕНИЕ. Интегрируем почленно: - где С1 – произвольная постоянная.
10. Еще раз интегрируем: Таким образом, решение ДУ принципиально неоднозначно, поскольку в него входят произвольные постоянные.
11. ДУ задает семейство интегральных кривых на плоскости.
12. Общим решением ДУ (1) называется решение y=φ(x,C1,…,Cn)
13. В рассмотренном примере - общее решение; - частное решение;

21. 1. ПОНЯТИЕ ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ Дифференциальным уравнением (ДУ) называется уравнение, связывающее искомую функцию одной или нескольких переменных и производные различных порядков этой функции.

Главная
Математика
Дифференциальные уравнения

Слайд 121. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ

Слайд 221. 1. ПОНЯТИЕ ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ
Дифференциальным уравнением (ДУ)
называется уравнение, связывающее
искомую функцию одной

или нескольких
переменных и производные различных
порядков этой функции.

Слайд 3Если искомая функция зависит от одной
переменной, то ДУ называется обыкновенным.
Если искомая

функция зависит от нескольких
переменных, то ДУ называется уравнением
в частных производных.

Слайд 4Простейшим примером ДУ является задача о нахождении первообразной F(x) для заданной

функции f(x), т.к. ее можно рассматривать как задачу решения уравнения:

Слайд 5В общем случае ДУ можно записать:

1
Порядок старшей производной, входящей
в ДУ, называется

порядком ДУ.

Слайд 6Например, дифференциальное уравнение
является уравнением третьего порядка.
Решением ДУ (1) называется такая
функция y=y(x),

которая при подстановке
ее в это уравнение обращает его
в тождество.

Слайд 7Например, решением дифференциального уравнения
является функция
поскольку
Подставляем в уравнение:

Слайд 8ПРИМЕР.
Решить дифференциальное уравнение:

Слайд 9РЕШЕНИЕ.
Интегрируем почленно:
- где С1 – произвольная постоянная.

Слайд 10Еще раз интегрируем:
Таким образом, решение ДУ принципиально
неоднозначно, поскольку в него входят
произвольные

постоянные.

Слайд 11ДУ задает семейство интегральных кривых на плоскости. Для выделения определенной интегральной

кривой достаточно задать точку, через которую проходит искомая кривая и направление, в котором она проходит через эту точку. Такие условия называются начальными.
Например, если в рассмотренном примере

то

Слайд 12Общим решением ДУ (1) называется решение
y=φ(x,C1,…,Cn)
которое является функцией переменной х и
произвольных

независимых постоянных.

Частным решением ДУ (1) называется
решение, полученное из общего решения при
конкретных числовых значениях
постоянных.

Слайд 13В рассмотренном примере
- общее решение;
- частное решение;

Скачать презентацию

Дифференциальные уравнения презентация

Содержание

Слайд 121. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ

Слайд 221. 1. ПОНЯТИЕ ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ
Дифференциальным уравнением (ДУ)
называется уравнение, связывающее
искомую функцию одной

Слайд 3Если искомая функция зависит от одной
переменной, то ДУ называется обыкновенным.
Если искомая

Слайд 4Простейшим примером ДУ является задача о нахождении первообразной F(x) для заданной

Слайд 5В общем случае ДУ можно записать:

1
Порядок старшей производной, входящей
в ДУ, называется

Слайд 6Например, дифференциальное уравнение
является уравнением третьего порядка.
Решением ДУ (1) называется такая
функция y=y(x),

Слайд 7Например, решением дифференциального уравнения
является функция
поскольку
Подставляем в уравнение:

Слайд 8ПРИМЕР.
Решить дифференциальное уравнение:

Слайд 9РЕШЕНИЕ.
Интегрируем почленно:
- где С1 – произвольная постоянная.

Слайд 10Еще раз интегрируем:
Таким образом, решение ДУ принципиально
неоднозначно, поскольку в него входят
произвольные

Слайд 11ДУ задает семейство интегральных кривых на плоскости. Для выделения определенной интегральной

Слайд 12Общим решением ДУ (1) называется решение
y=φ(x,C1,…,Cn)
которое является функцией переменной х и
произвольных

Слайд 13В рассмотренном примере
- общее решение;
- частное решение;

Обратная связь

Что такое ThePresentation.ru?

Дифференциальные уравнения презентация

Содержание

Слайд 121. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ

Слайд 221. 1. ПОНЯТИЕ ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯДифференциальным уравнением (ДУ)называется уравнение, связывающееискомую функцию одной

Слайд 3Если искомая функция зависит от однойпеременной, то ДУ называется обыкновенным.Если искомая

Слайд 4Простейшим примером ДУ является задача о нахождении первообразной F(x) для заданной

Слайд 5В общем случае ДУ можно записать:1Порядок старшей производной, входящейв ДУ, называется

Слайд 6Например, дифференциальное уравнениеявляется уравнением третьего порядка.Решением ДУ (1) называется такаяфункция y=y(x),

Слайд 7Например, решением дифференциального уравненияявляется функция посколькуПодставляем в уравнение:

Слайд 8ПРИМЕР.Решить дифференциальное уравнение:

Слайд 9РЕШЕНИЕ.Интегрируем почленно: - где С1 – произвольная постоянная.

Слайд 10Еще раз интегрируем:Таким образом, решение ДУ принципиальнонеоднозначно, поскольку в него входятпроизвольные

Слайд 11ДУ задает семейство интегральных кривых на плоскости. Для выделения определенной интегральной

Слайд 12Общим решением ДУ (1) называется решениеy=φ(x,C1,…,Cn)которое является функцией переменной х ипроизвольных

Слайд 13В рассмотренном примере- общее решение;- частное решение;

Похожие презентации

Обратная связь

Что такое ThePresentation.ru?

Слайд 221. 1. ПОНЯТИЕ ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ
Дифференциальным уравнением (ДУ)
называется уравнение, связывающее
искомую функцию одной

Слайд 3Если искомая функция зависит от одной
переменной, то ДУ называется обыкновенным.
Если искомая

Слайд 5В общем случае ДУ можно записать:

1
Порядок старшей производной, входящей
в ДУ, называется

Слайд 6Например, дифференциальное уравнение
является уравнением третьего порядка.
Решением ДУ (1) называется такая
функция y=y(x),

Слайд 7Например, решением дифференциального уравнения
является функция
поскольку
Подставляем в уравнение:

Слайд 8ПРИМЕР.
Решить дифференциальное уравнение:

Слайд 9РЕШЕНИЕ.
Интегрируем почленно:
- где С1 – произвольная постоянная.

Слайд 10Еще раз интегрируем:
Таким образом, решение ДУ принципиально
неоднозначно, поскольку в него входят
произвольные

Слайд 12Общим решением ДУ (1) называется решение
y=φ(x,C1,…,Cn)
которое является функцией переменной х и
произвольных

Слайд 13В рассмотренном примере
- общее решение;
- частное решение;