- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Новые типы обратных связей в системах автоматического управления презентация
Содержание
- 1. Новые типы обратных связей в системах автоматического управления
- 2. О возникновении т.н. «теории робастных систем»
- 3. Классификация простейших случаев неопределенности по видам характеристических
- 4. Постановка задачи: где
- 5. Хорошо бы расследовать 1. Координатно-операторная обратная
- 6. 1. Координатно-операторная обратная связь 1.1. Система
- 7. t=time; init x1=1,x2=0,Miu_cp=0; ao=5; w=0.5; K=10; d=2;
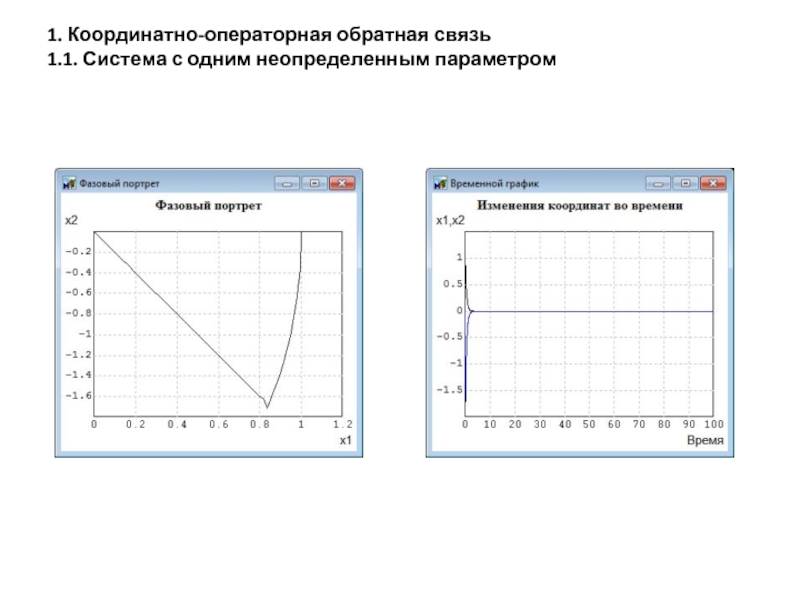
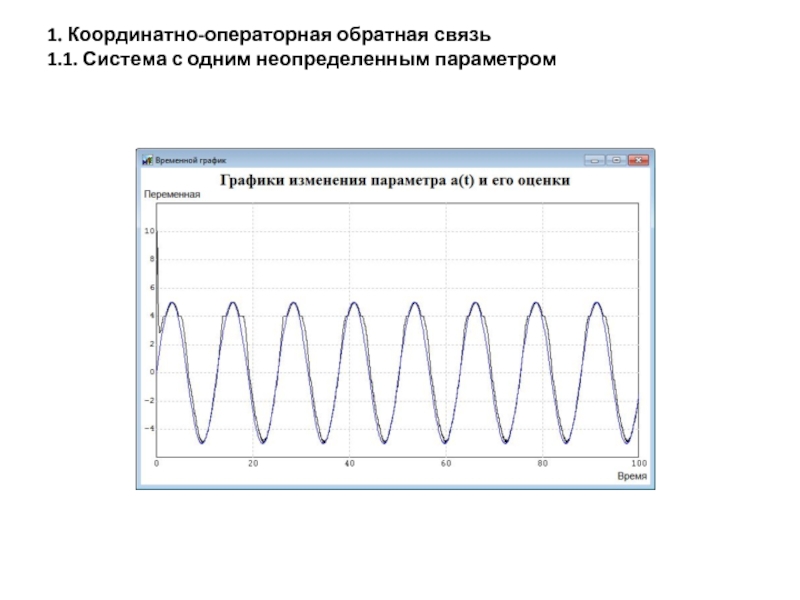
- 8. 1. Координатно-операторная обратная связь 1.1. Система с одним неопределенным параметром
- 9. 1. Координатно-операторная обратная связь 1.1. Система с одним неопределенным параметром
- 10. Сделаем замену переменных 1. Координатно-операторная
- 11. где d характеризует качество стабилизации. Проведем следующие
- 12. Если Е>0 то для стабилизации требуется
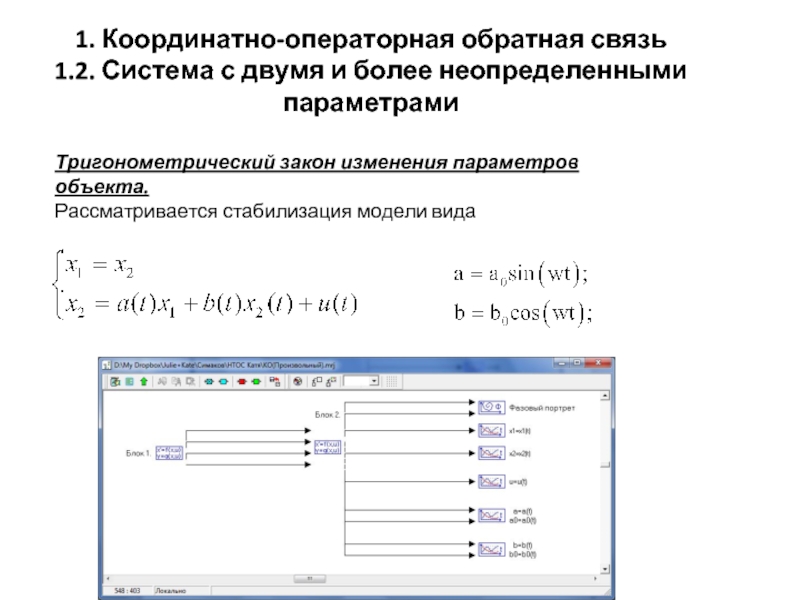
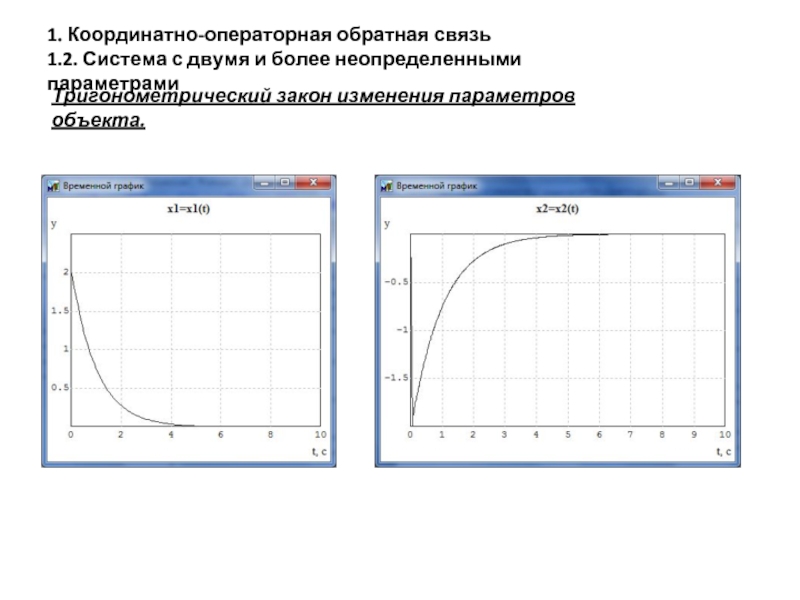
- 13. Тригонометрический закон изменения параметров объекта.
- 14. 1. Координатно-операторная
- 15. 1. Координатно-операторная
- 16. Тригонометрический закон изменения параметров
- 17. , где 1. Координатно-операторная обратная связь 1.2.
- 18. 1. Координатно-операторная обратная связь 1.2. Система с
- 19. 1. Координатно-операторная обратная связь 1.2. Система с
- 20. 1. Координатно-операторная обратная связь 1.2. Система с
- 21. 1. Координатно-операторная обратная связь 1.2. Система с
- 22. ,где 1. Координатно-операторная обратная связь
- 23. 1. Координатно-операторная обратная связь 1.2. Система с
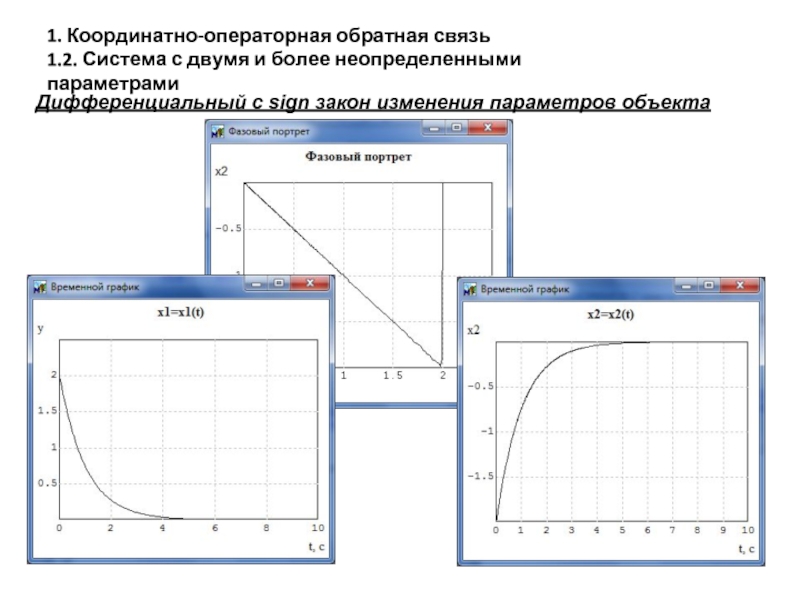
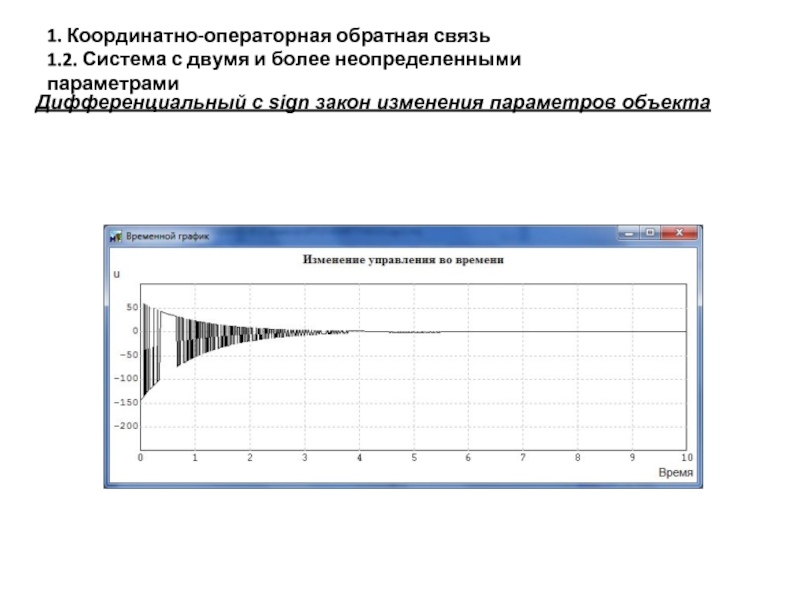
- 24. Дифференциальный с sign закон изменения параметров объекта
- 25. Дифференциальный с sign закон изменения параметров объекта
- 26. Дифференциальный с sign закон изменения параметров объекта
- 27. 1. Координатно-операторная обратная связь 1.3. Система,
- 28. 1. Координатно-операторная обратная связь 1.3. Система,
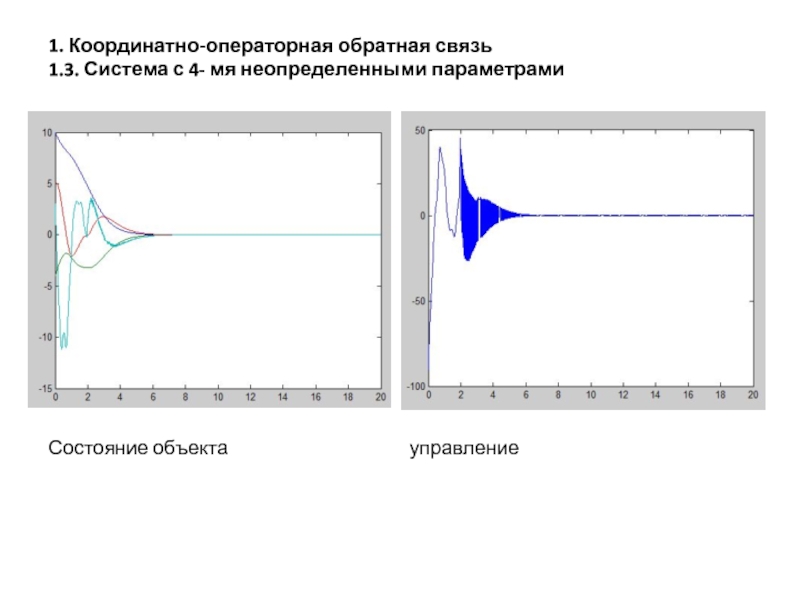
- 29. 1. Координатно-операторная обратная связь 1.3. Система с 4- мя неопределенными параметрами Состояние объекта управление
- 30. в отличие от п. 3,
- 31. 2. Операторная обратная связь 2.1. Система с
- 32. 2. Операторная обратная связь 2.2. Система с
- 33. 2. Операторная обратная связь 2.2. Система с
- 34. 2. Операторная обратная связь 2.2. Система с
- 35. 2. Операторная обратная связь 2.2. Система с
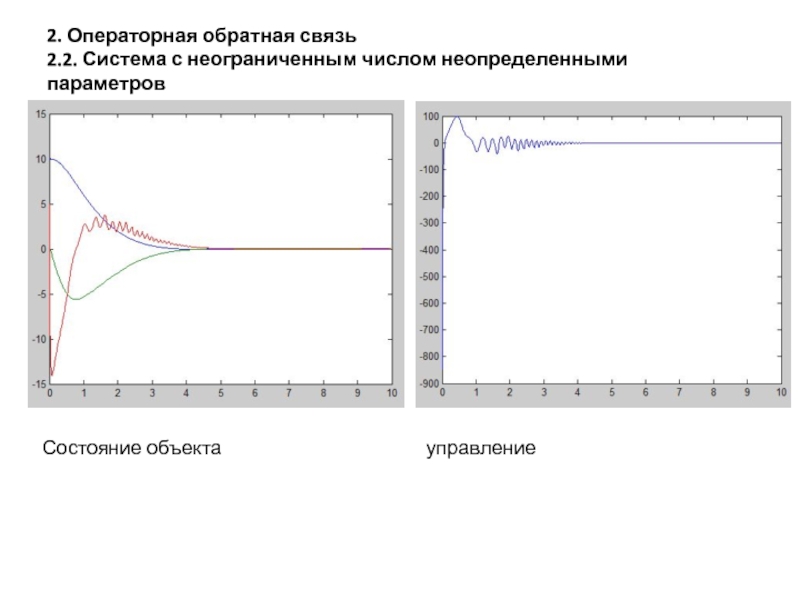
- 36. 2. Операторная обратная связь 2.2. Система с неограниченным числом неопределенными параметров Состояние объекта управление
Слайд 2О возникновении т.н. «теории робастных систем»
Основополагающей работой, определившей возникновение теории робастности,
(«Асимптотическая устойчивость положения равновесия семейства систем дифференциальных уравнений» - Дифференциальные уравнения. – 1978. – №11. – С.2086-2088.)
Теорема Харитонова имеет важный и
красивый результат.
Но наряду с этим имеет и ограничение.
Слайд 3Классификация простейших случаев неопределенности по видам характеристических полиномов для линейных стационарных
Интервальная неопределенность – коэффициенты полинома являются интервальными параметрами;
Аффинная неопределенность – коэффициенты полинома образованы суммой или разностью интервальных параметров;
Полилинейная неопределенность – коэффициенты полинома линейно зависят от каждого параметра, если остальные параметры фиксированы;
Полиномиальная неопределенность – коэффициенты полинома зависят полиномиально хотя бы от одного параметра.
Для интервальной и аффинной неопределенностей существуют достаточно простые методы анализа и синтеза, но если коэффициенты полинома являются более сложными функциями интервальных параметров, то анализ и синтез ИС значительно усложняется.
Слайд 5Хорошо бы расследовать
1. Координатно-операторная обратная связь
1.1. Система с одним неопределенным параметром
1.2.
1.3 Система с более, чем двумя неопределенными параметрами
2.1 Операторная обратная связь с одним неопределенным параметром
2.2 Операторная обратная связь более чем с одним неопределенным параметром
Слайд 6
1. Координатно-операторная обратная связь
1.1. Система с одним неопределенным параметром
«Хрестоматийный» пример
скаляризуем
Теперь имеем дело со скалярным объектом:
Будем рассматривать стабилизацию в малом
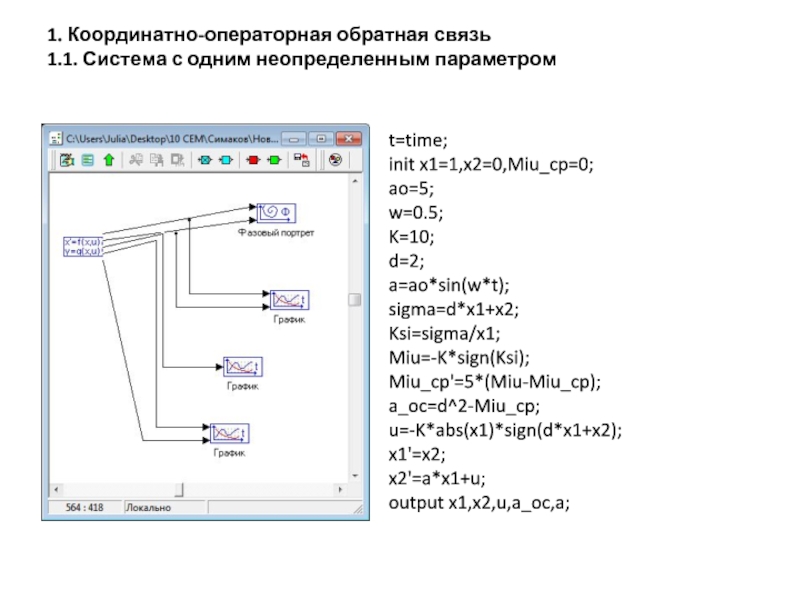
Слайд 7t=time;
init x1=1,x2=0,Miu_cp=0;
ao=5;
w=0.5;
K=10;
d=2;
a=ao*sin(w*t);
sigma=d*x1+x2;
Ksi=sigma/x1;
Miu=-K*sign(Ksi);
Miu_cp'=5*(Miu-Miu_cp);
a_oc=d^2-Miu_cp;
u=-K*abs(x1)*sign(d*x1+x2);
x1'=x2;
x2'=a*x1+u;
output x1,x2,u,a_oc,a;
1. Координатно-операторная обратная связь
1.1. Система с одним неопределенным параметром
Слайд 10
Сделаем замену переменных
1. Координатно-операторная обратная связь
1.2. Система с двумя и более
Слайд 11где d характеризует качество стабилизации.
Проведем следующие преобразования
Тогда система уравнений примет вид
1.
1.2. Система с двумя и более неопределенными параметрами
Слайд 12Если Е>0 то для стабилизации требуется
Для того чтобы
1.
1.2. Система с двумя и более неопределенными параметрами
Если Е<0 то для стабилизации требуется
То есть Е-d попадает в корневой промежуток рассматриваемого выражения
Слайд 13
Тригонометрический закон изменения параметров объекта.
Рассматривается стабилизация модели вида
1. Координатно-операторная обратная связь
1.2.
Слайд 14
1. Координатно-операторная обратная связь
1.2. Система с двумя и более неопределенными параметрами
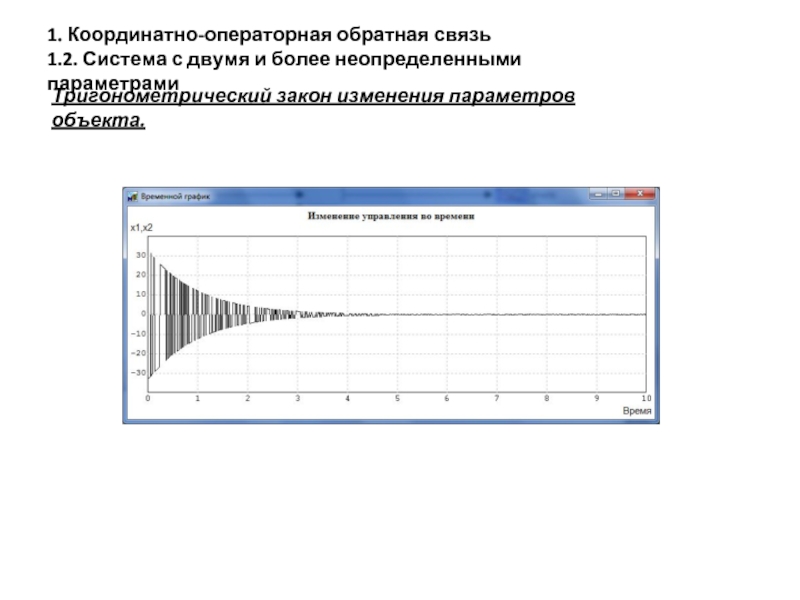
Тригонометрический
Слайд 15
1. Координатно-операторная обратная связь
1.2. Система с двумя и более неопределенными параметрами
Тригонометрический
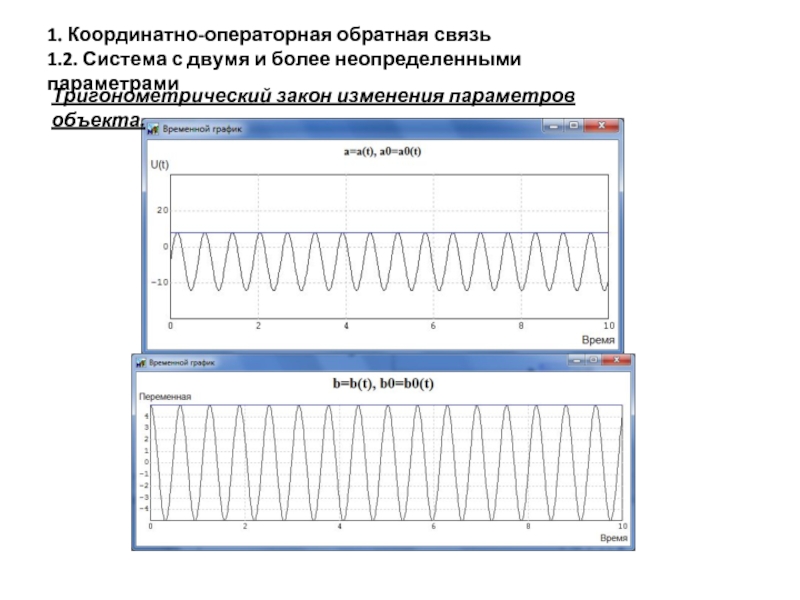
Слайд 16
Тригонометрический закон изменения параметров объекта.
1. Координатно-операторная обратная связь
1.2. Система с двумя
Слайд 17, где
1. Координатно-операторная обратная связь
1.2. Система с двумя и более неопределенными
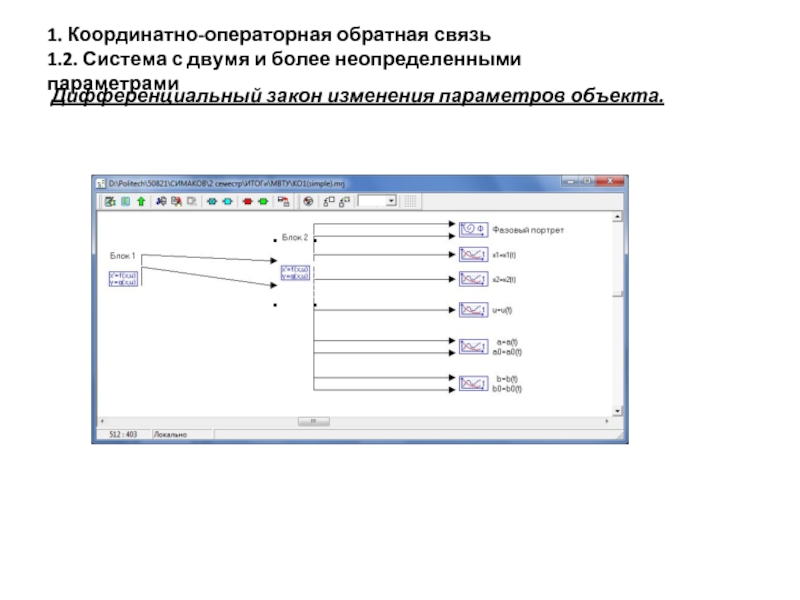
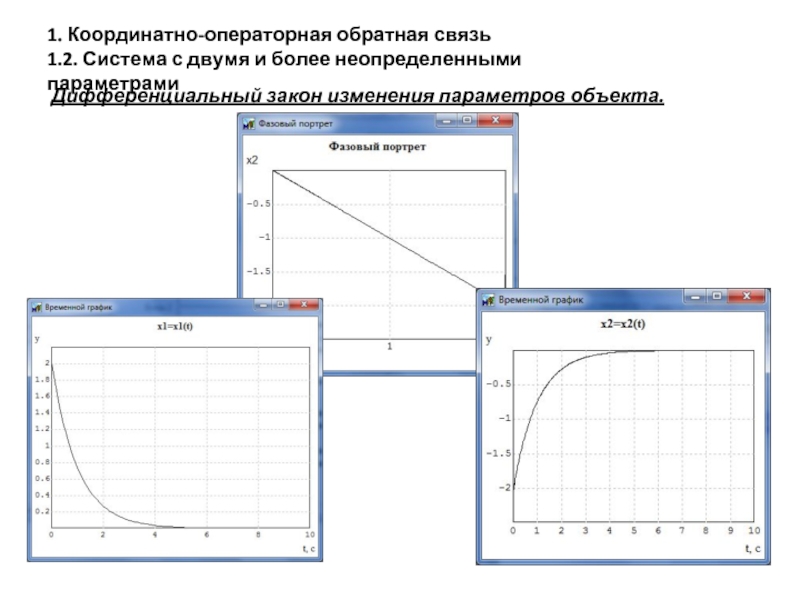
Дифференциальный закон изменения параметров объекта.
Слайд 181. Координатно-операторная обратная связь
1.2. Система с двумя и более неопределенными параметрами
Дифференциальный
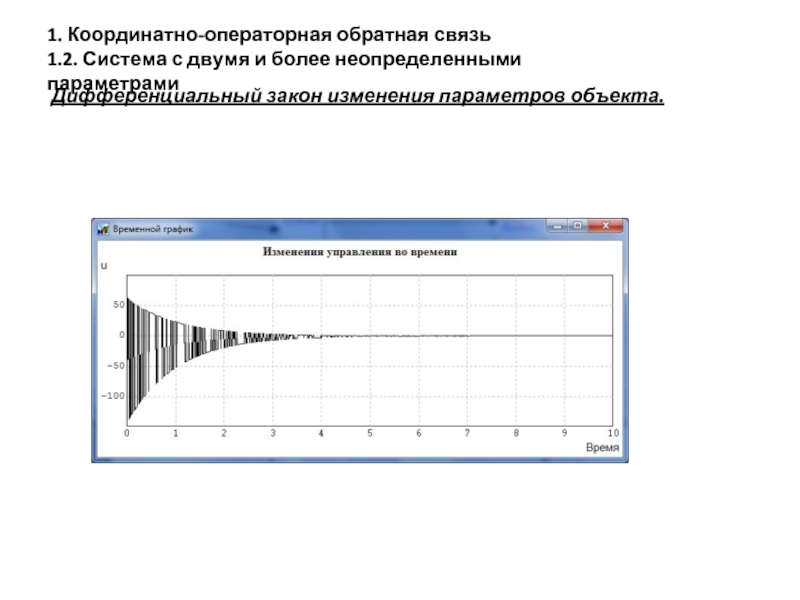
Слайд 191. Координатно-операторная обратная связь
1.2. Система с двумя и более неопределенными параметрами
Дифференциальный
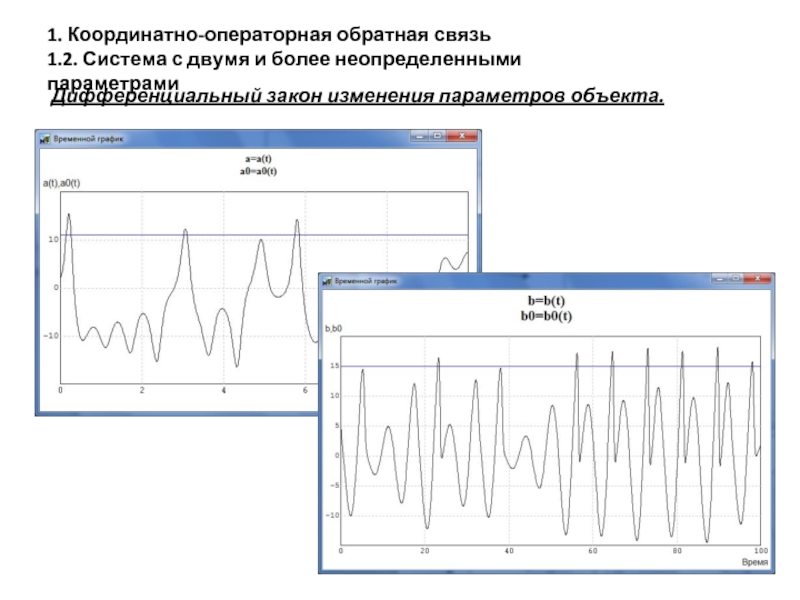
Слайд 201. Координатно-операторная обратная связь
1.2. Система с двумя и более неопределенными параметрами
Дифференциальный
Слайд 211. Координатно-операторная обратная связь
1.2. Система с двумя и более неопределенными параметрами
Дифференциальный
Слайд 22,где
1. Координатно-операторная обратная связь
1.2. Система с двумя и более неопределенными параметрами
Дифференциальный
Слайд 231. Координатно-операторная обратная связь
1.2. Система с двумя и более неопределенными параметрами
Дифференциальный
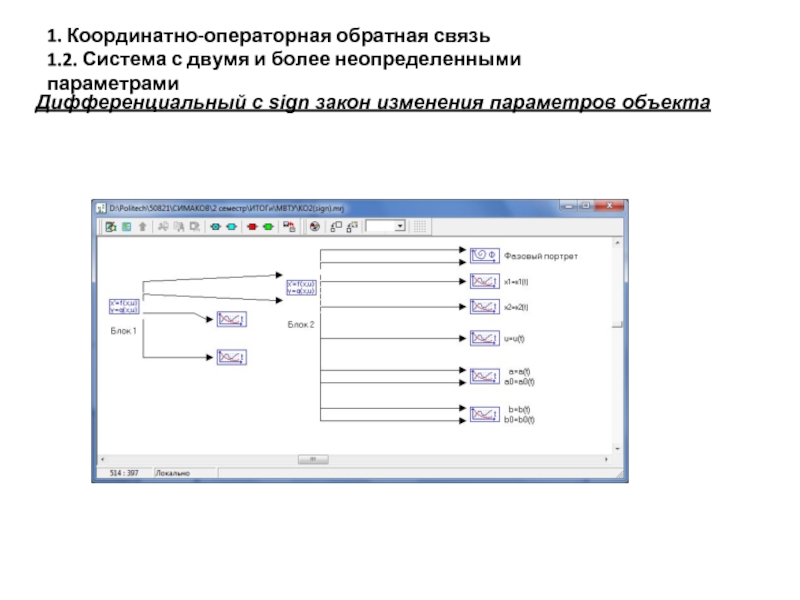
Слайд 24Дифференциальный с sign закон изменения параметров объекта
1. Координатно-операторная обратная связь
1.2. Система
Слайд 25Дифференциальный с sign закон изменения параметров объекта
1. Координатно-операторная обратная связь
1.2. Система
Слайд 26Дифференциальный с sign закон изменения параметров объекта
1. Координатно-операторная обратная связь
1.2. Система
Слайд 27
1. Координатно-операторная обратная связь
1.3. Система, представленная в «Фробениусовой» форме с неограниченным
Введем новую переменную характеризующую отклонение объекта от требуемого режима
Слайд 28
1. Координатно-операторная обратная связь
1.3. Система, представленная в Фробениусовой форме с неограниченным
Стоит задача стабилизации сигма в нуле и выбора коэффициентов
Слайд 291. Координатно-операторная обратная связь
1.3. Система с 4- мя неопределенными параметрами
Состояние объекта
управление
Слайд 30
в отличие от п. 3, вводим координатную ошибку следующим соотношением
2. Операторная
2.1. Система с одним неопределенными параметрами
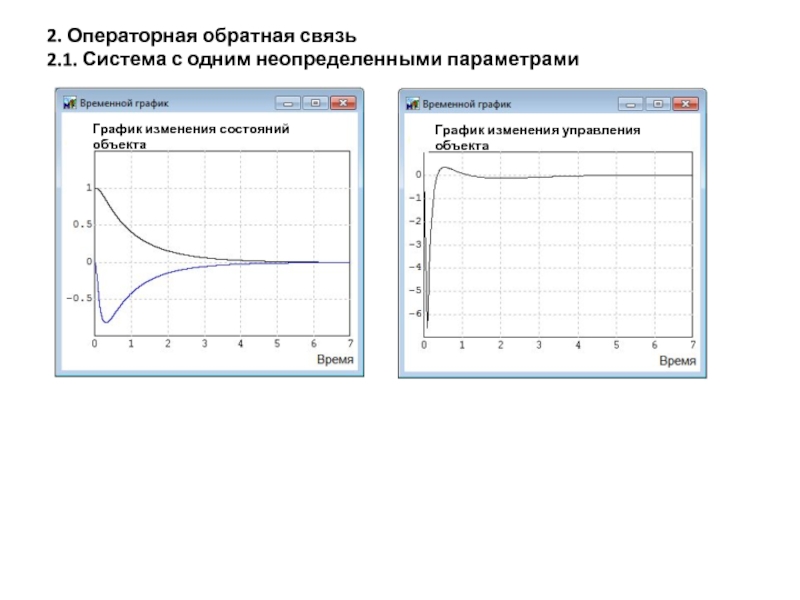
Слайд 312. Операторная обратная связь
2.1. Система с одним неопределенными параметрами
График изменения состояний
График изменения управления объекта
Слайд 322. Операторная обратная связь
2.2. Система с неограниченным числом неопределенными параметров
Заметим что
т.е. являются коэффициентами «характеристического» полинома(точнее его аналога):
Будем искать управление в следующем виде u=Kx
Слайд 332. Операторная обратная связь
2.2. Система с неограниченным числом неопределенными параметров
Тогда уравнение
стабилизация системы с заданным качеством d
Характеристический полином имеет вид :
Необходимым условие стабилизации с заданным качеством ОУ является не отрицательность коэффициентов последнего характеристического уравнения
Найдем оценки этих коэффициентов
Слайд 342. Операторная обратная связь
2.2. Система с неограниченным числом неопределенными параметров
Теперь можно
Слайд 352. Операторная обратная связь
2.2. Система с неограниченным числом неопределенными параметров
Произведем синтез