- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Алгоритмы нахождения независимого множества презентация
Содержание
- 1. Алгоритмы нахождения независимого множества
- 2. ФОРМУЛИРОВКА ЗАДАЧИ Дано: неориентированный граф G (V
- 3. ФОРМУЛИРОВКА ЗАДАЧИ Дано: неориентированный граф G (V
- 4. ФОРМУЛИРОВКА ЗАДАЧИ Дано: неориентированный граф G (V
- 5. МЕТОД ПОЛНОГО ПЕРЕБОРА Алгоритм полного перебора проверяет
- 6. МЕТОД ПОЛНОГО ПЕРЕБОРА Алгоритм проверяет каждую вершину
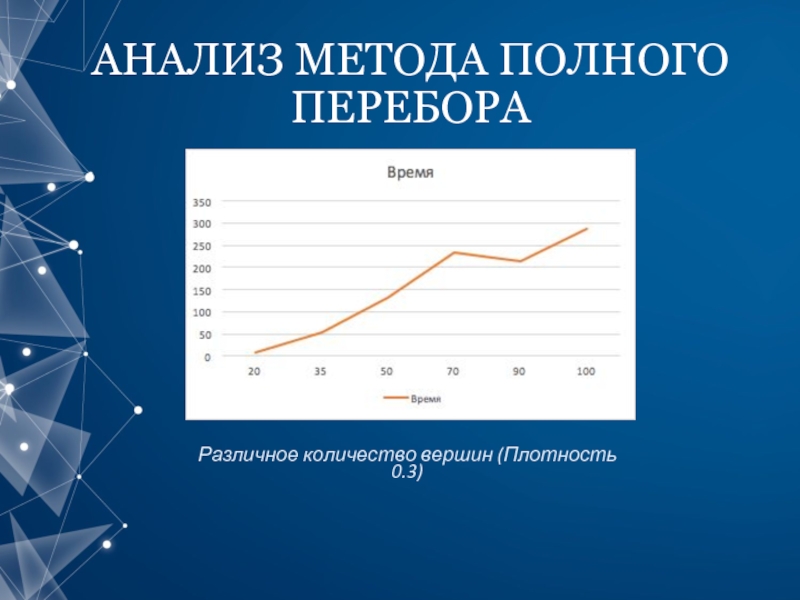
- 7. АНАЛИЗ МЕТОДА ПОЛНОГО ПЕРЕБОРА Различное количество вершин (Плотность 0.3)
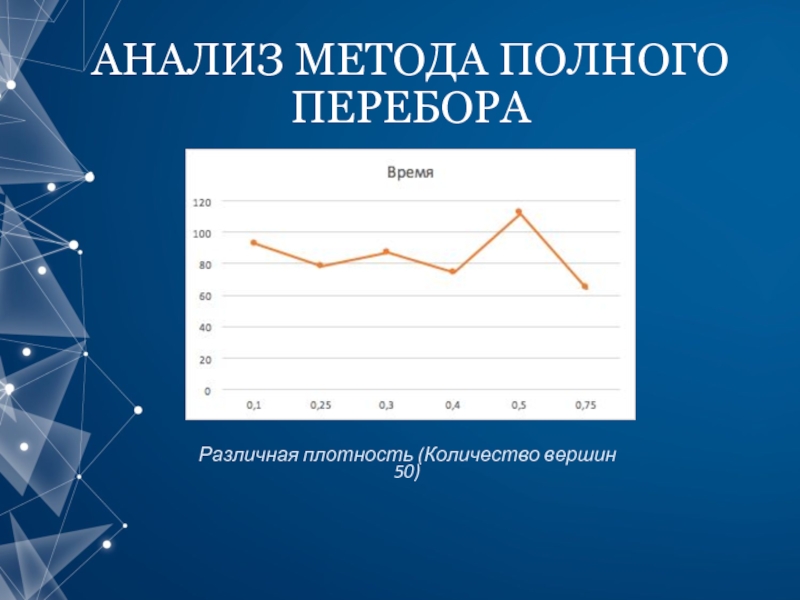
- 8. АНАЛИЗ МЕТОДА ПОЛНОГО ПЕРЕБОРА Различная плотность (Количество вершин 50)
- 9. АЛГОРИТМ БРОНА-КЕРБОША Способом уменьшения количества
- 10. АЛГОРИТМ БРОНА-КЕРБОША На каждом шаге
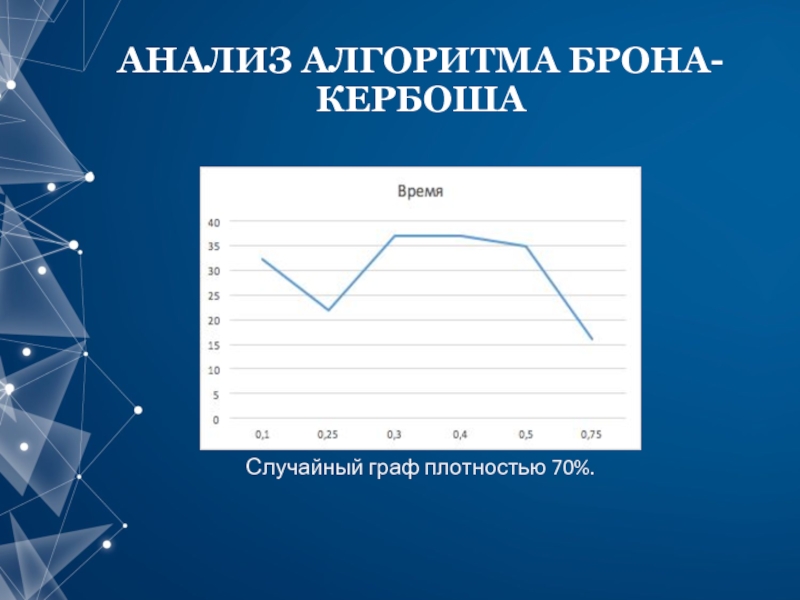
- 11. АНАЛИЗ АЛГОРИТМА БРОНА-КЕРБОША Случайный граф плотностью 70%.
- 12. АНАЛИЗ АЛГОРИТМА БРОНА-КЕРБОША Различная плотность (Количество вершин 50)
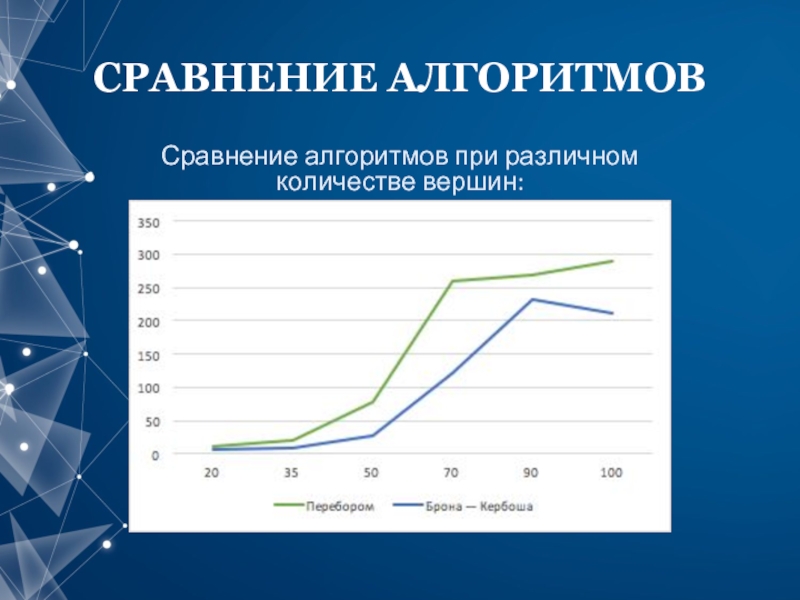
- 13. СРАВНЕНИЕ АЛГОРИТМОВ Сравнение алгоритмов при различном количестве вершин:
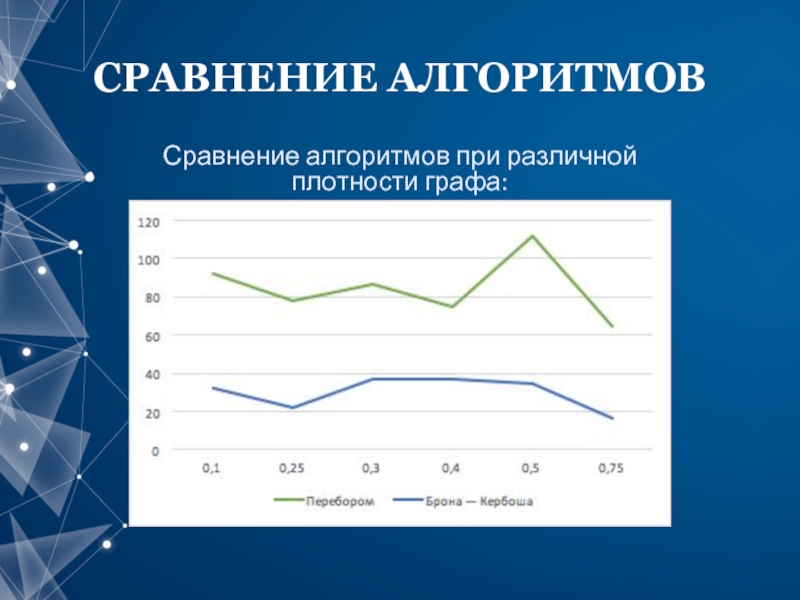
- 14. СРАВНЕНИЕ АЛГОРИТМОВ Сравнение алгоритмов при различной плотности графа:
- 15. ВЫВОД На основании проведенного исследования можно сделать
- 16. Курсовая работа Алгоритмы нахождения независимого множества Круглов Владислав Сулейманова Алина Митрофанова Екатерина
Слайд 1Курсовая работа
Алгоритмы нахождения независимого множества
Круглов Владислав
Сулейманова Алина
Митрофанова Екатерина
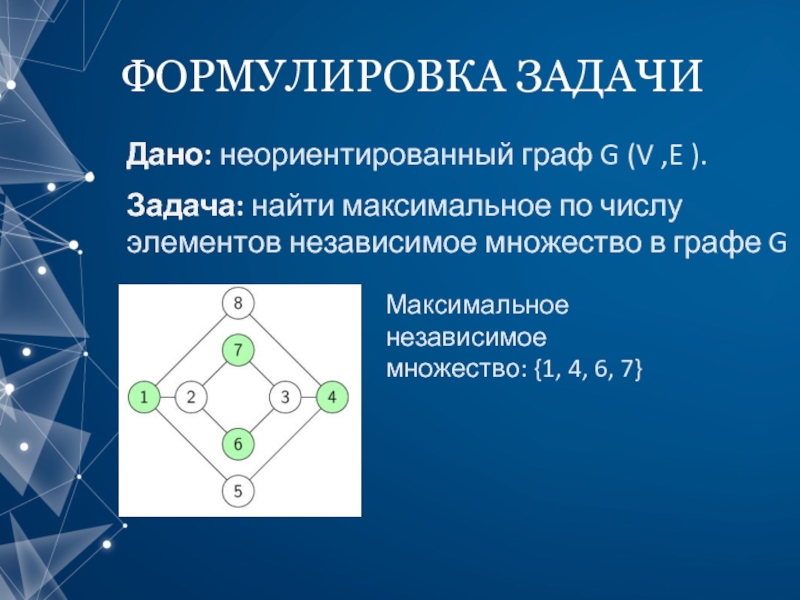
Слайд 2ФОРМУЛИРОВКА ЗАДАЧИ
Дано: неориентированный граф G (V ,E ).
Задача: найти максимальное по
Максимальное независимое
множество: {1, 4, 6, 7}
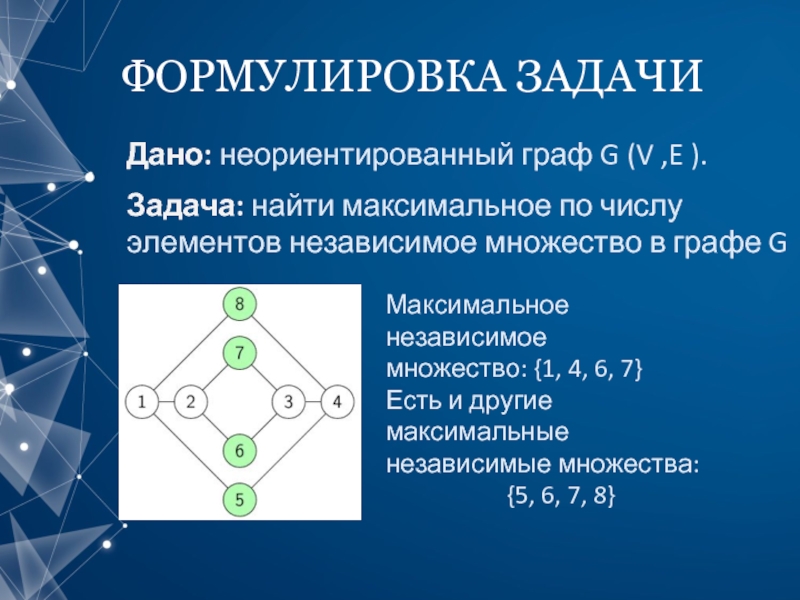
Слайд 3ФОРМУЛИРОВКА ЗАДАЧИ
Дано: неориентированный граф G (V ,E ).
Задача: найти максимальное по
Максимальное независимое
множество: {1, 4, 6, 7}
Есть и другие максимальные
независимые множества:
{5, 6, 7, 8}
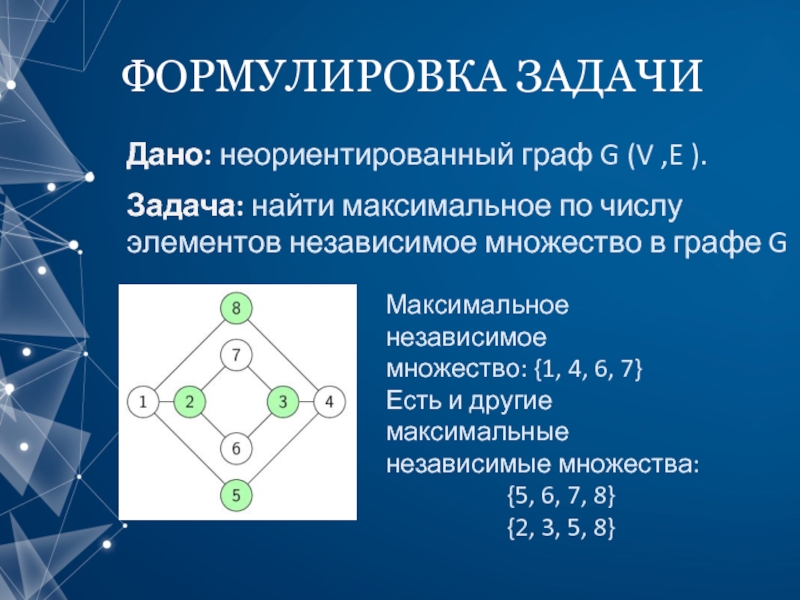
Слайд 4ФОРМУЛИРОВКА ЗАДАЧИ
Дано: неориентированный граф G (V ,E ).
Задача: найти максимальное по
Максимальное независимое
множество: {1, 4, 6, 7}
Есть и другие максимальные
независимые множества:
{5, 6, 7, 8}
{2, 3, 5, 8}
Слайд 5МЕТОД ПОЛНОГО ПЕРЕБОРА
Алгоритм полного перебора проверяет все подмножества вершин, являются ли
Слайд 6МЕТОД ПОЛНОГО ПЕРЕБОРА
Алгоритм проверяет каждую вершину на независимость с другими вершинами
Каждое найденное множество необходимо проверять на максимальную независимость.
Для этого нужно определять, является ли оно подмножеством какого-либо другого найденного независимого множества.
Вычислительная сложность полного перебора O(n2 2n).
Слайд 9АЛГОРИТМ
БРОНА-КЕРБОША
Способом уменьшения количества рассматриваемых вариантов является поиск с возвращением,
Находит все максимальные по включению независимые множества.
Слайд 10АЛГОРИТМ
БРОНА-КЕРБОША
На каждом шаге алгоритма множество V разбито на четыре
M — текущее независимое множество;
Γ(M) — множество вершин, смежных с M;
K – множество кандидатов, т. е. вершин, каждая из которых может быть добавлена в M;
P – множество просмотренных вершин, каждая из которых не может быть добавлена в текущее M, так как уже добавлялась ранее.