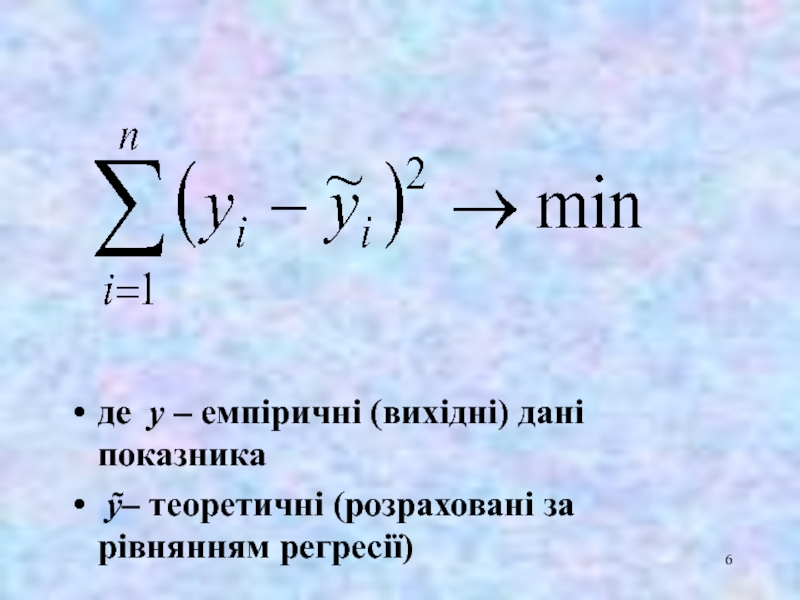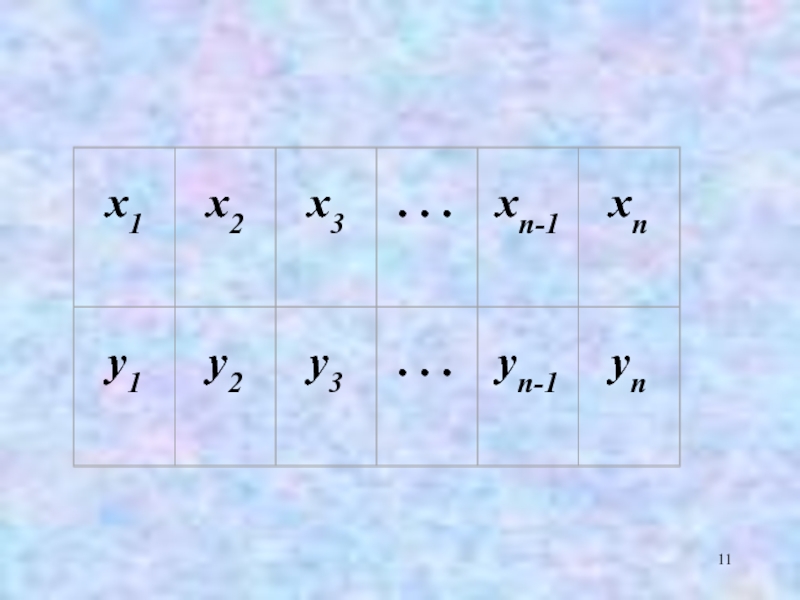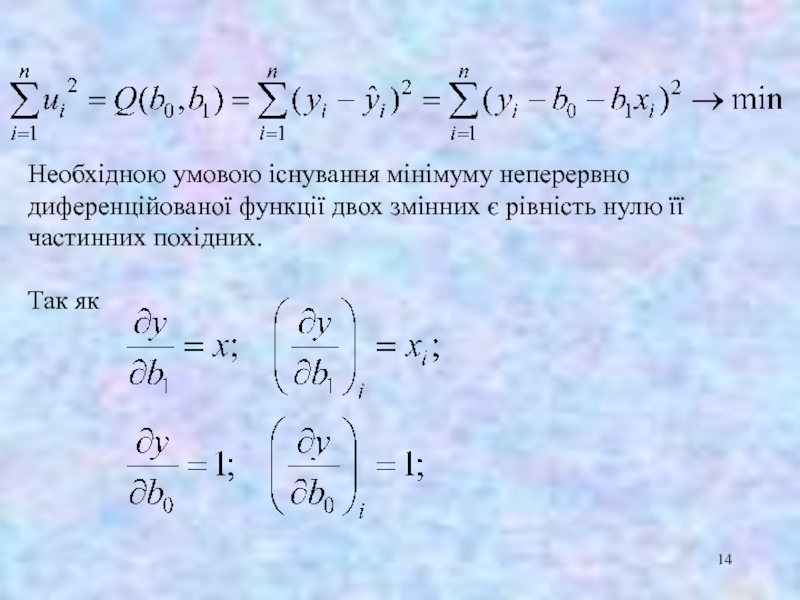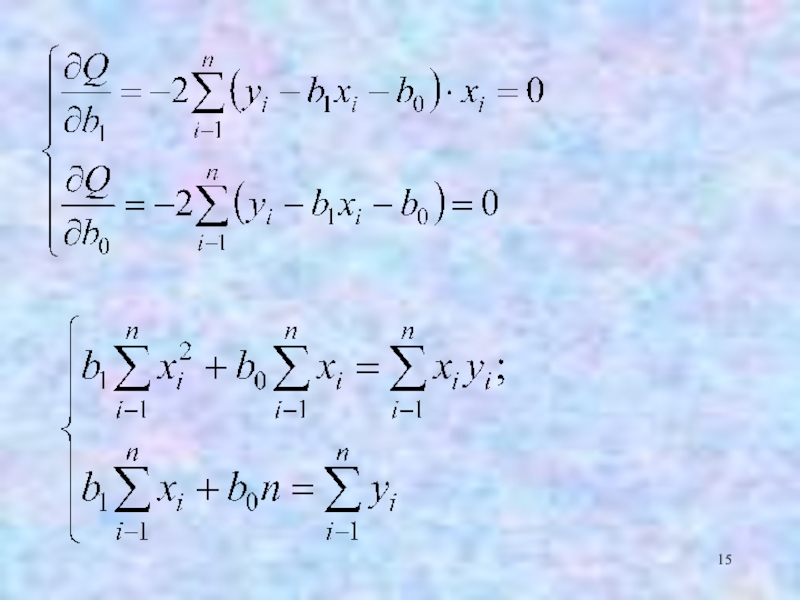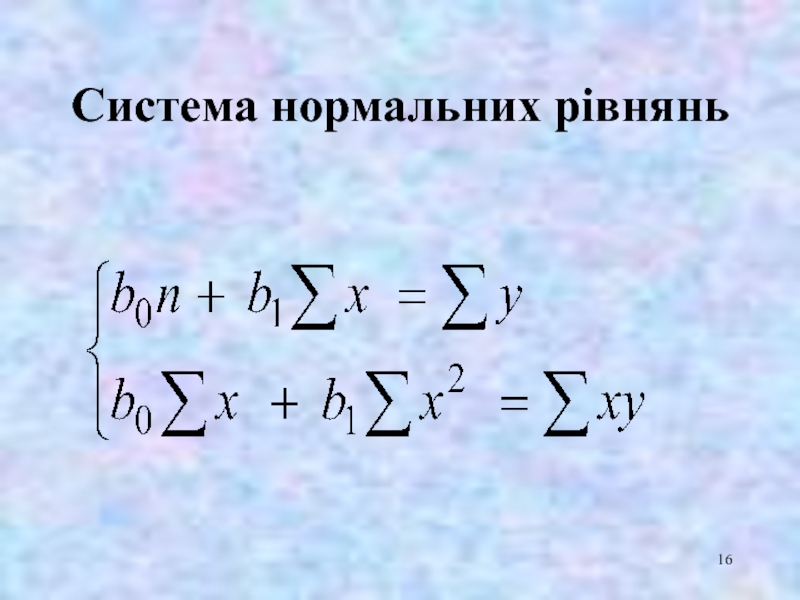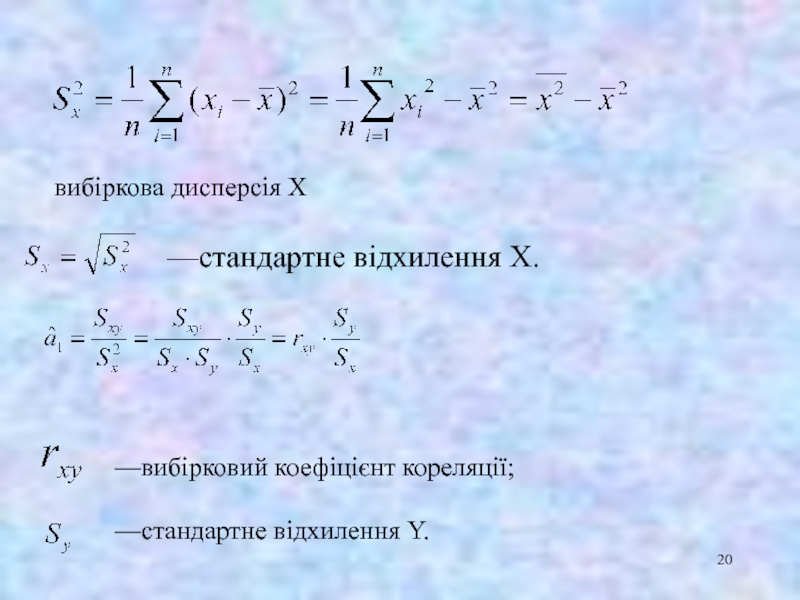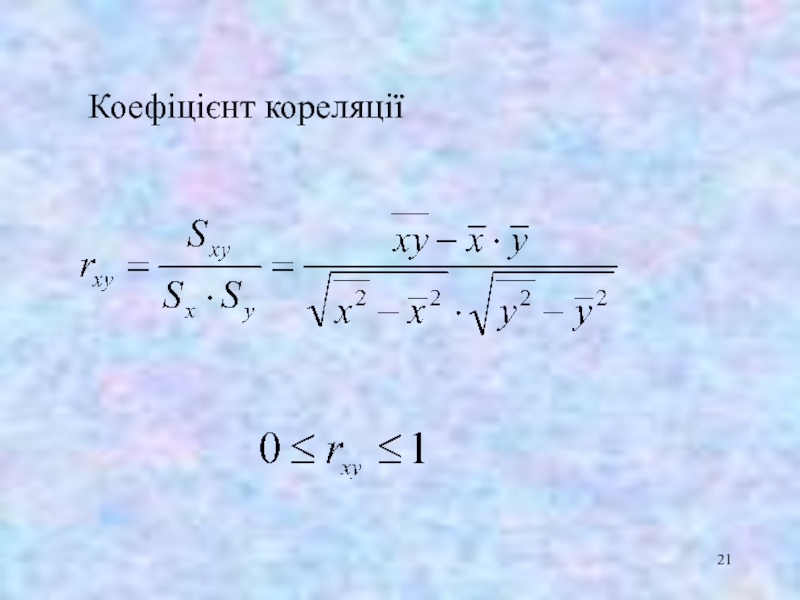Тема 4
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Метод найменших квадратів. (Тема 4) презентация
Содержание
- 1. Метод найменших квадратів. (Тема 4)
- 2. План 4.1. Суть методу найменших квадратів
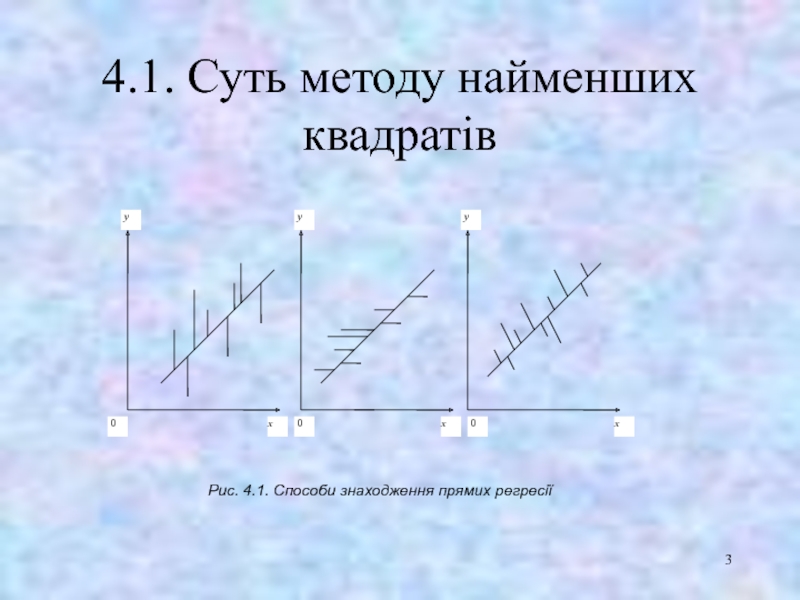
- 3. 4.1. Суть методу найменших квадратів Рис. 4.1. Способи знаходження прямих регресії
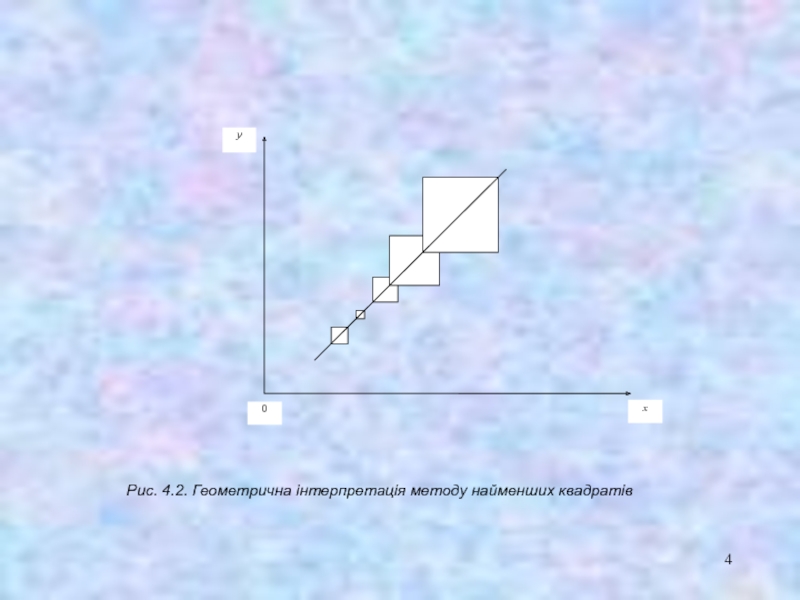
- 4. Рис. 4.2. Геометрична інтерпретація методу найменших квадратів
- 5. Суть методу найменших квадратів (МНК) полягає у
- 6. де
- 7. 4.2. Передумови застосування МНК 1) Існує лінійний
- 8. 2) Факторна змінна x є детерміністичною (невипадковою)
- 9. 4.3. Система нормальних рівнянь Будемо вважати, що
- 10. У загальному випадку nарна лінійна регресія є
- 12. метод найменших модулів (МНМ). метод найменших квадратів (МНК).
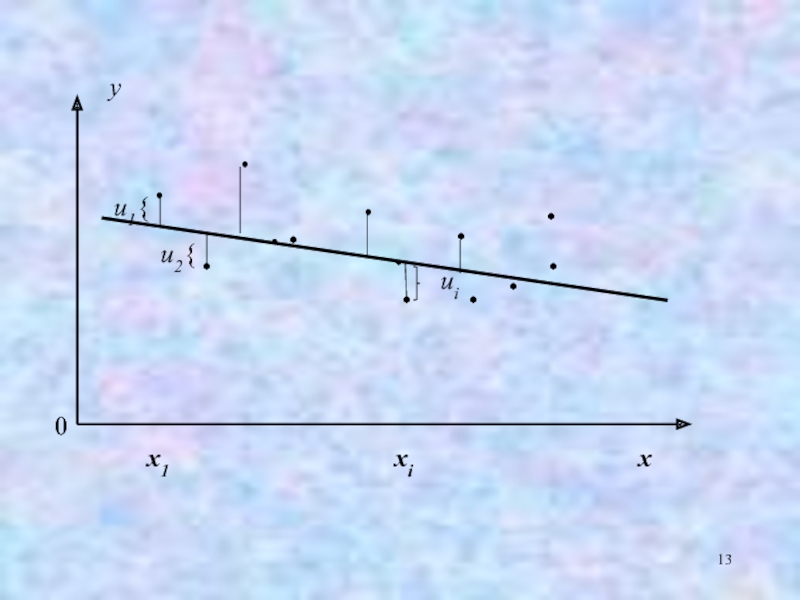
- 13. y x x1 . . . .
- 14. Необхідною умовою існування мінімуму неперервно диференційованої
- 16. Система нормальних рівнянь
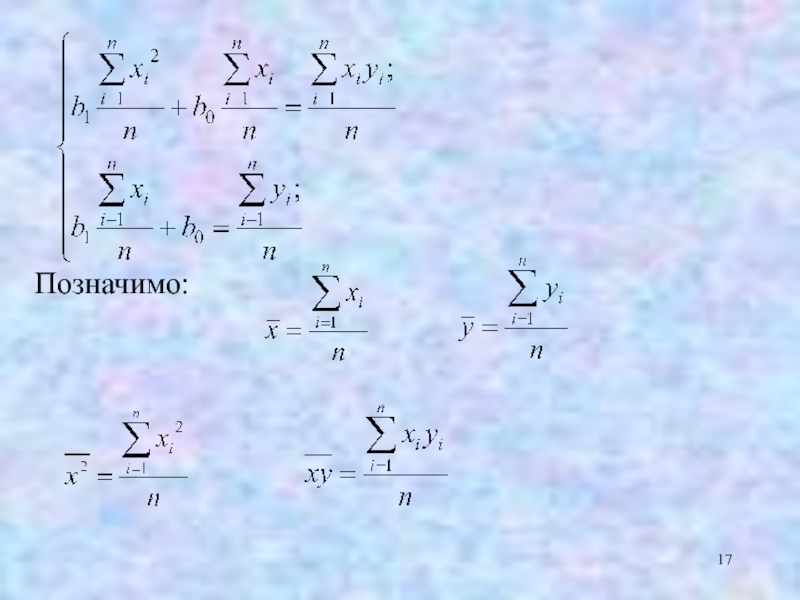
- 17. Позначимо:
- 18. одержимо звідки маємо
- 19. Неважко помітити, що
- 20. вибіркова дисперсія X —стандартне відхилення
- 21. Коефіцієнт кореляції
Слайд 1Метод найменших квадратів
Лектор: к.е.н., доц., доцент кафедри вищої математики, економетрії і
статистики ДЕМЧИШИН М.Я.
Слайд 2План
4.1. Суть методу найменших квадратів (МНК).
4.2. Передумови застосування МНК.
4.3. Система нормальних
рівнянь.
Слайд 5Суть методу найменших квадратів (МНК)
полягає у знаходженні такої теоретичної лінії регресії,
яка в порівнянні з іншими проходить найближче до емпіричної лінії регресії,
тобто дає
найменшу суму квадратів відхилень фактичних значень результативної ознаки від розрахункових (теоретичних) значень
тобто дає
найменшу суму квадратів відхилень фактичних значень результативної ознаки від розрахункових (теоретичних) значень
Слайд 74.2. Передумови застосування МНК
1) Існує лінійний зв’язок між результуючою змінною у
та факторною змінною x, який описується рівняннями регресії
Слайд 82) Факторна змінна x є детерміністичною (невипадковою) величиною.
3) Математичне сподівання (середнє
значення) випадкового вектора дорівнює нулю, а дисперсія є невеликою постійною додатньою величиною, яка не залежить від індексу i, тобто
.
4) Компоненти вектора є некорельованими випадковими величинами, тобто для кожного
.
5) Часто вважають, що випадкова величина має нормальний закон розподілу з рівним нулю математичним сподіванням і постійною додатньою невеликою дисперсією
У даному випадку модель називається класичною нормальною лінійною регресійною моделлю.
Зауваження. У випадку класичної нормальної лінійної регресійної моделі умова 4 еквівалентна умові статистичної незалежності помилок .
.
4) Компоненти вектора є некорельованими випадковими величинами, тобто для кожного
.
5) Часто вважають, що випадкова величина має нормальний закон розподілу з рівним нулю математичним сподіванням і постійною додатньою невеликою дисперсією
У даному випадку модель називається класичною нормальною лінійною регресійною моделлю.
Зауваження. У випадку класичної нормальної лінійної регресійної моделі умова 4 еквівалентна умові статистичної незалежності помилок .
,
Слайд 94.3. Система нормальних рівнянь
Будемо вважати, що зв’язок між ознаками х та
у є лінійним і описується лінійним рівнянням регресії
(4.3)
де у – результуюча змінна; b0, b1– параметри рівняння регресії; х – факторна змінна; ε– випадкова величина.
(4.3)
де у – результуюча змінна; b0, b1– параметри рівняння регресії; х – факторна змінна; ε– випадкова величина.
Слайд 10У загальному випадку nарна лінійна регресія є лінійною функцією мiж залежною
змінною У i однiєю пояснюючою змінною Х:
Це спiввiдношення називається теоретичною лінійною регресiйною моделлю
b0 i b1 - теоретичні параметри
(теоретичні коефіцієнти) peгpeciї.
Це спiввiдношення називається теоретичною лінійною регресiйною моделлю
b0 i b1 - теоретичні параметри
(теоретичні коефіцієнти) peгpeciї.
Слайд 14
Необхідною умовою існування мінімуму неперервно диференційованої функції двох змінних є рівність
нулю її частинних похідних.
Так як
Так як
Слайд 19Неважко помітити, що можна обчислити
за формулою:
-вибірковий
кореляційний
момент випадкових
величин X і Y;
момент випадкових
величин X і Y;
Слайд 20
вибіркова дисперсія X
—стандартне відхилення X.
—вибірковий коефіцієнт кореляції;
—стандартне відхилення Y.