- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Взаимные положения прямой и плоскости, двух плоскостей. (Лекция 5) презентация
Содержание
- 1. Взаимные положения прямой и плоскости, двух плоскостей. (Лекция 5)
- 2. 5.1. Параллельность прямой и плоскости; двух
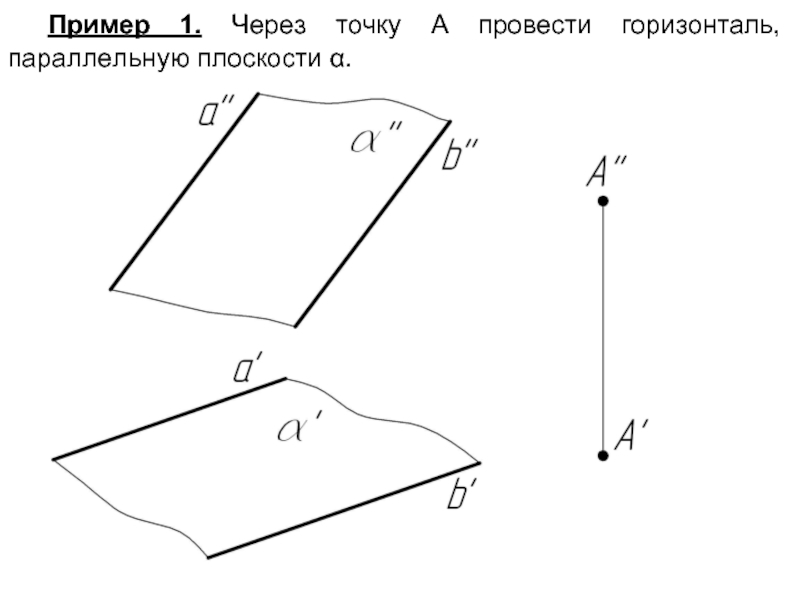
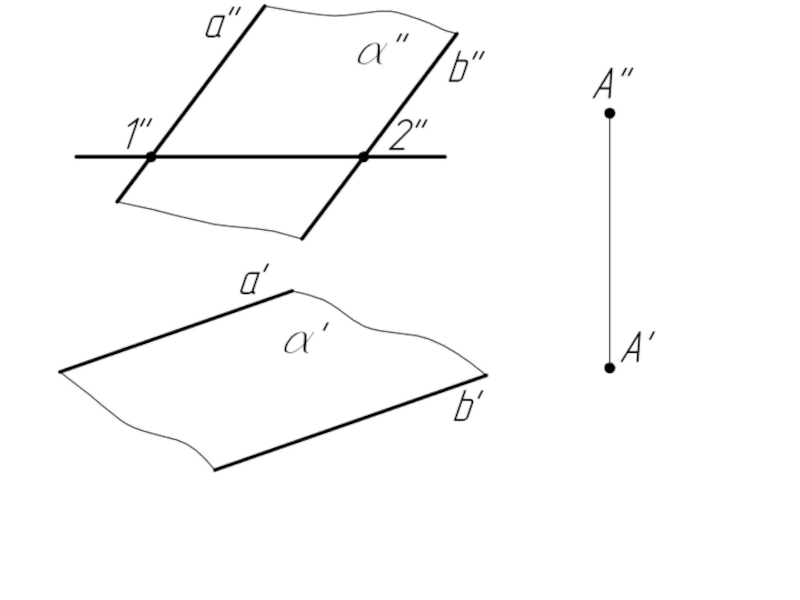
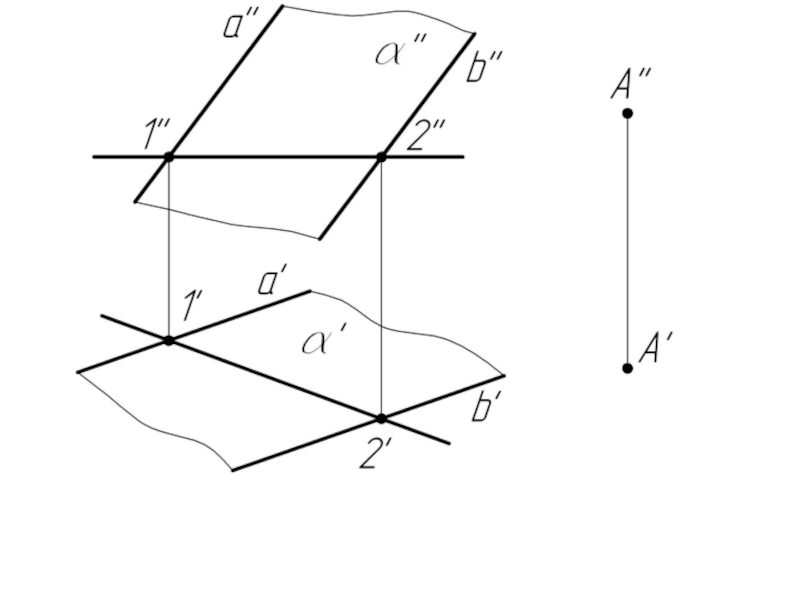
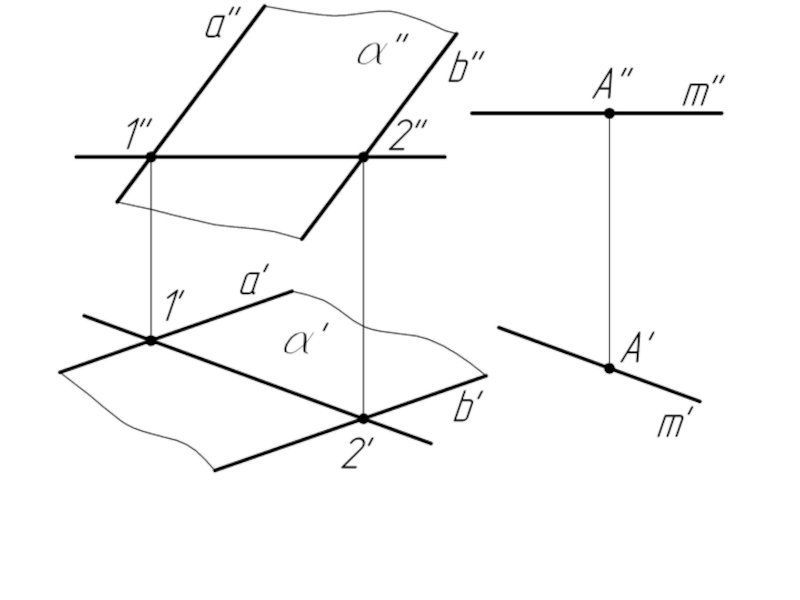
- 3. Пример 1. Через точку А провести горизонталь, параллельную плоскости α.
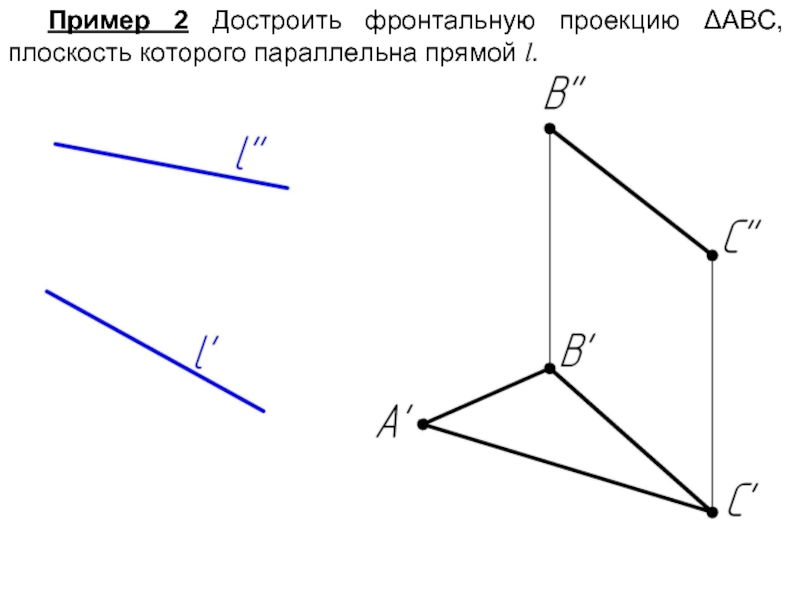
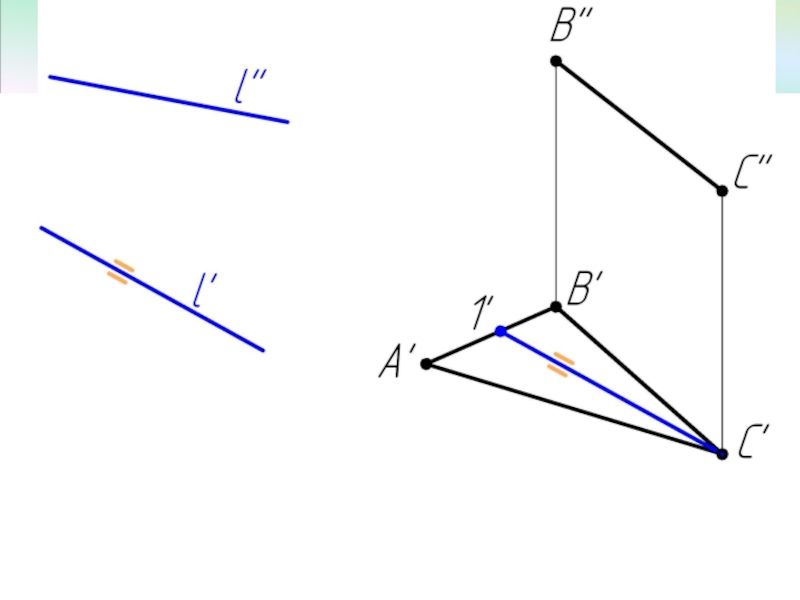
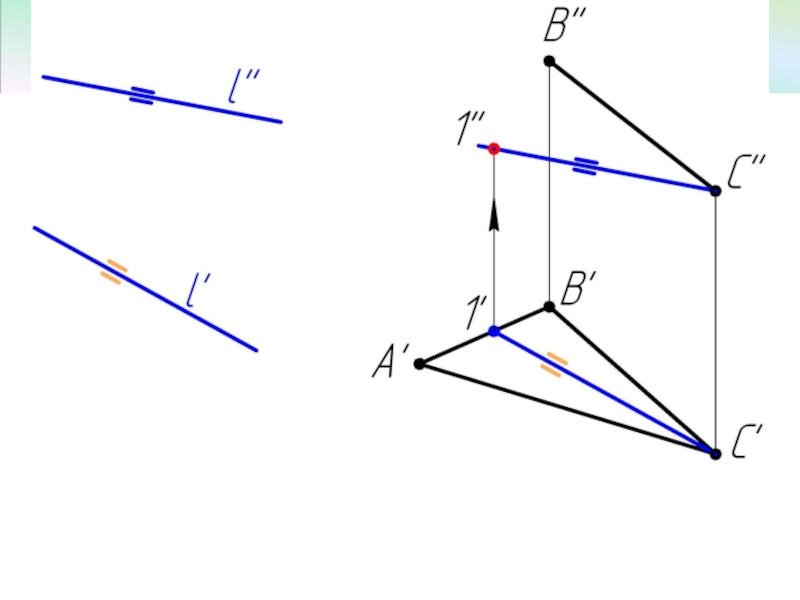
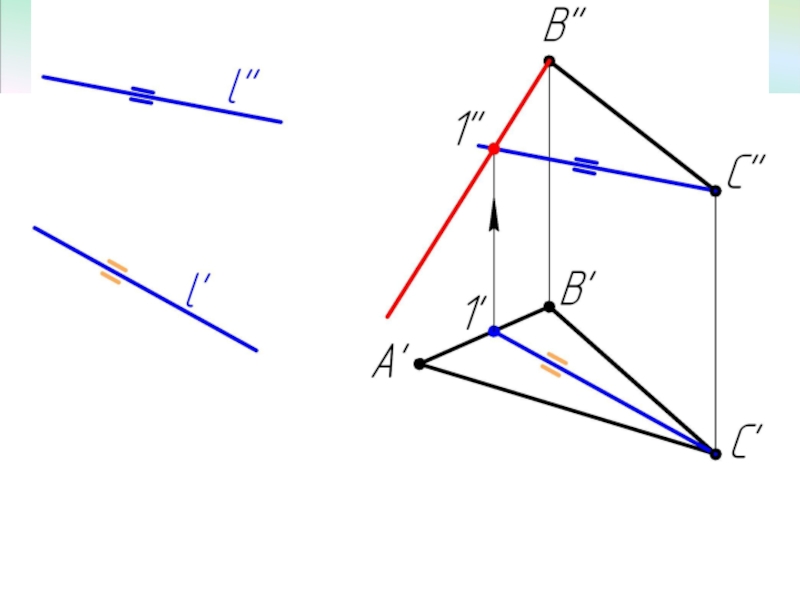
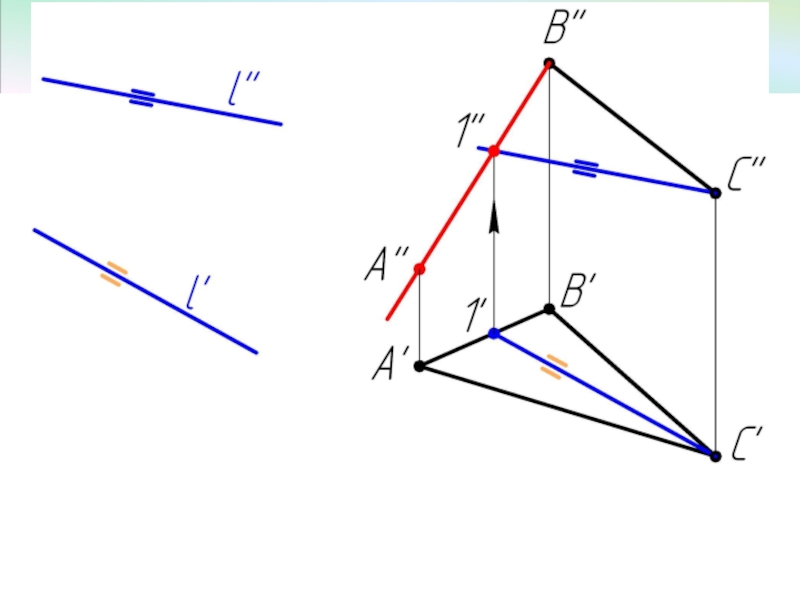
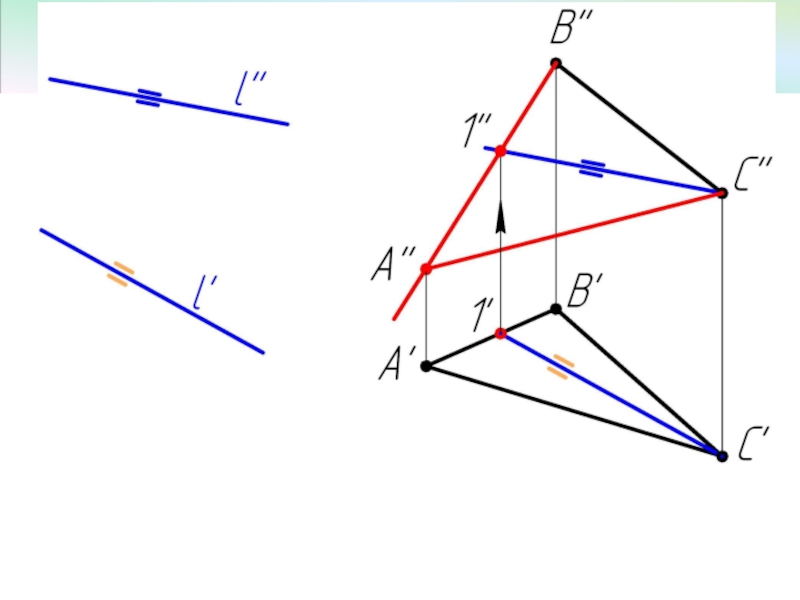
- 7. Пример 2 Достроить фронтальную проекцию ΔАВС, плоскость которого параллельна прямой l.
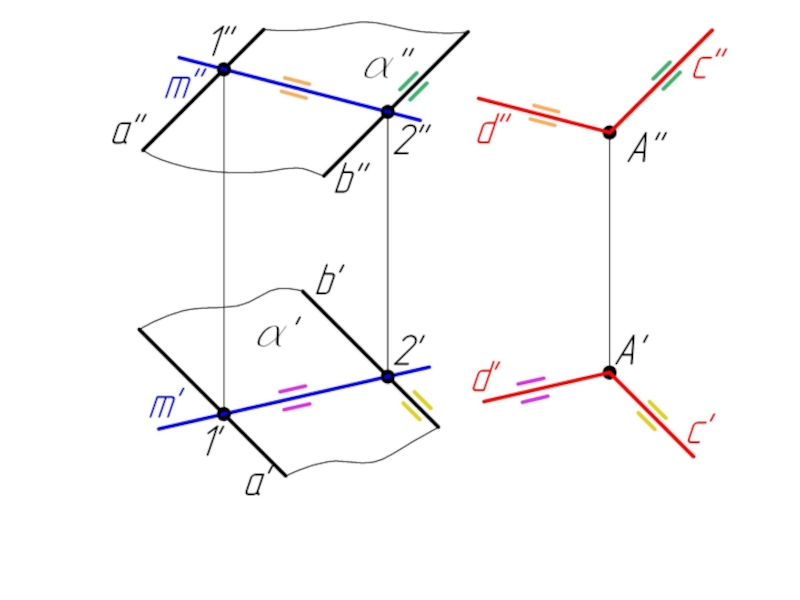
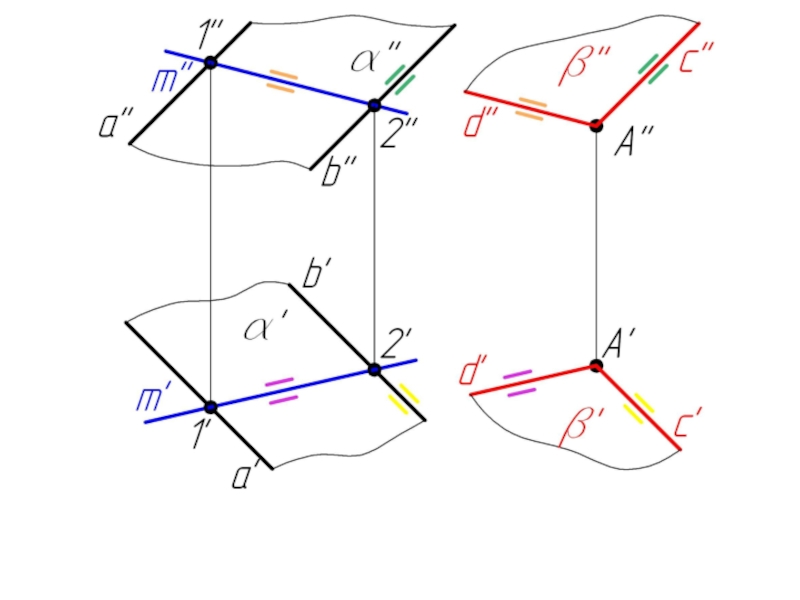
- 13. Две плоскости параллельны, если две пересекающиеся прямые
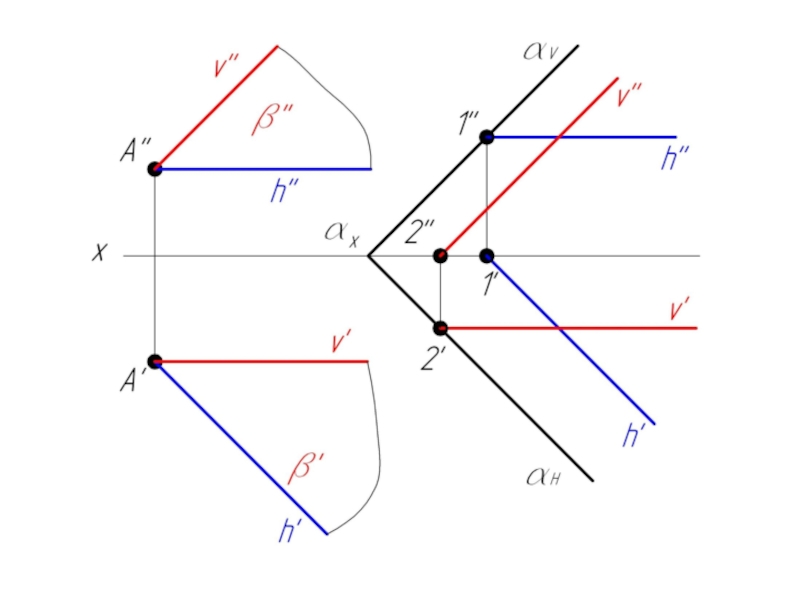
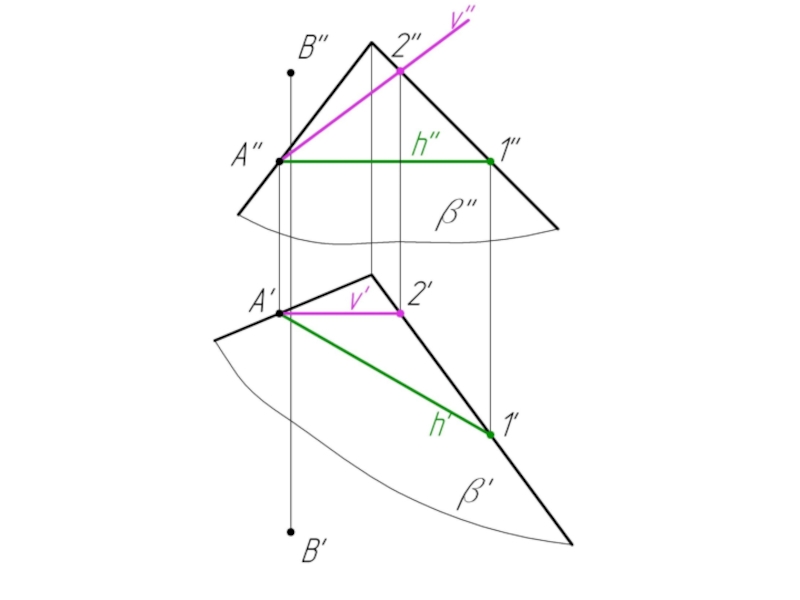
- 14. Пример 3. Через точку А провести плоскость β параллельную плоскости α.
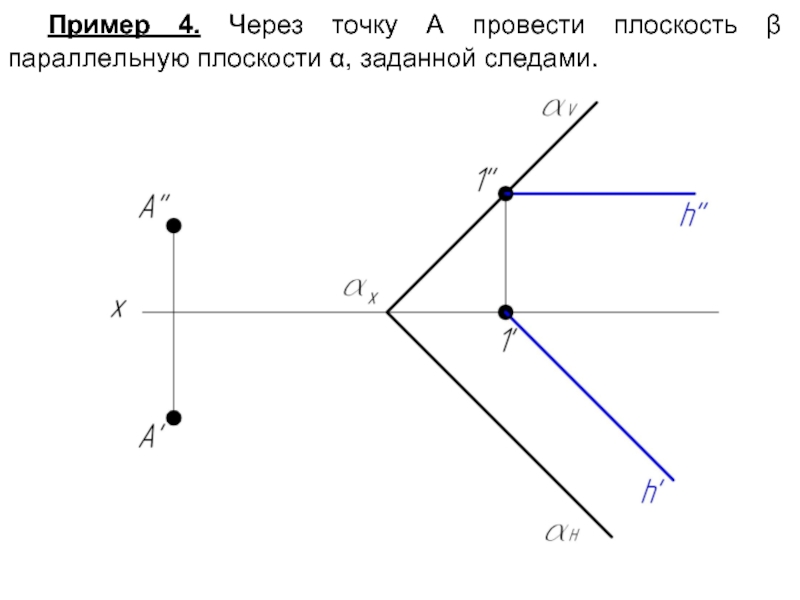
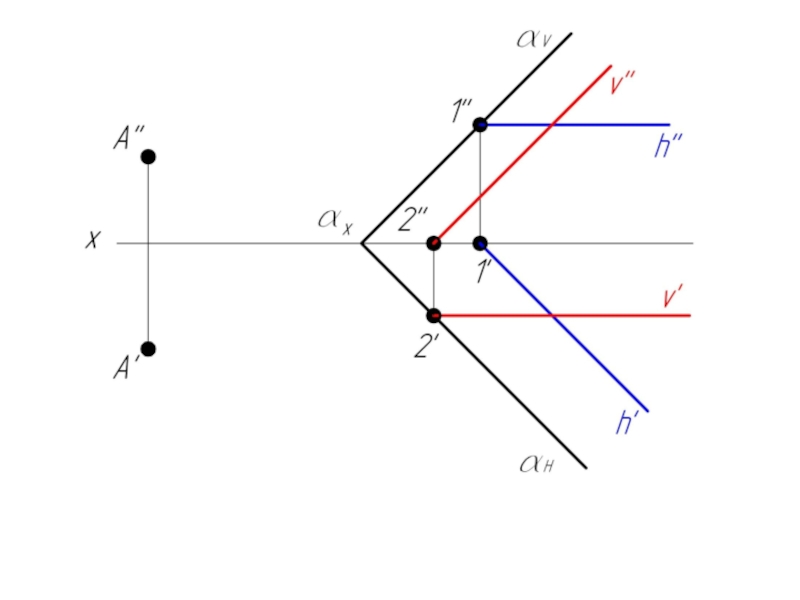
- 20. Пример 4. Через точку А провести плоскость β параллельную плоскости α, заданной следами.
- 23. 5.2. Пересечение прямой с плоскостью в общем
- 33. 5.3. Перпендикулярность прямой и плоскости
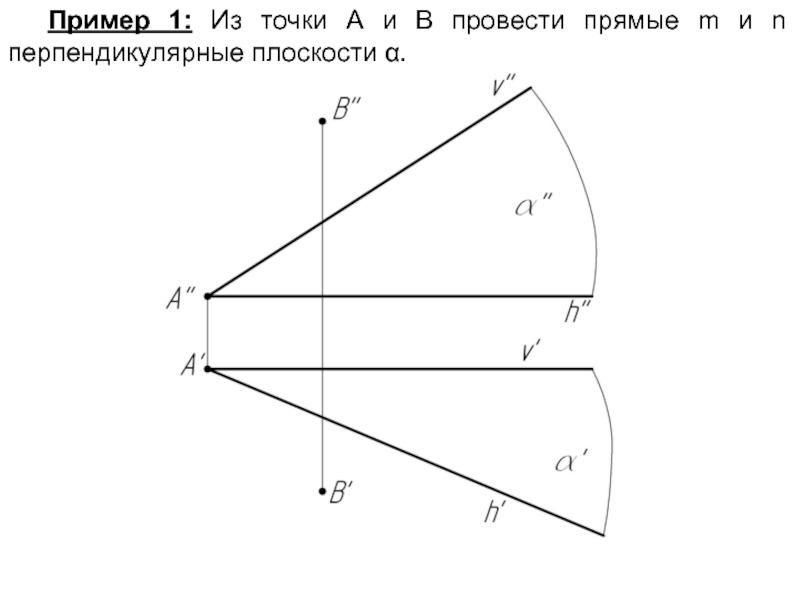
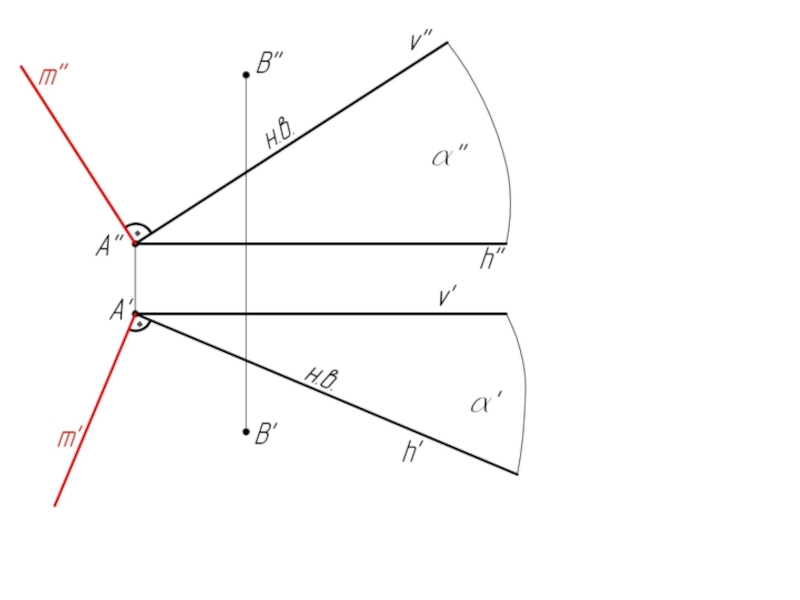
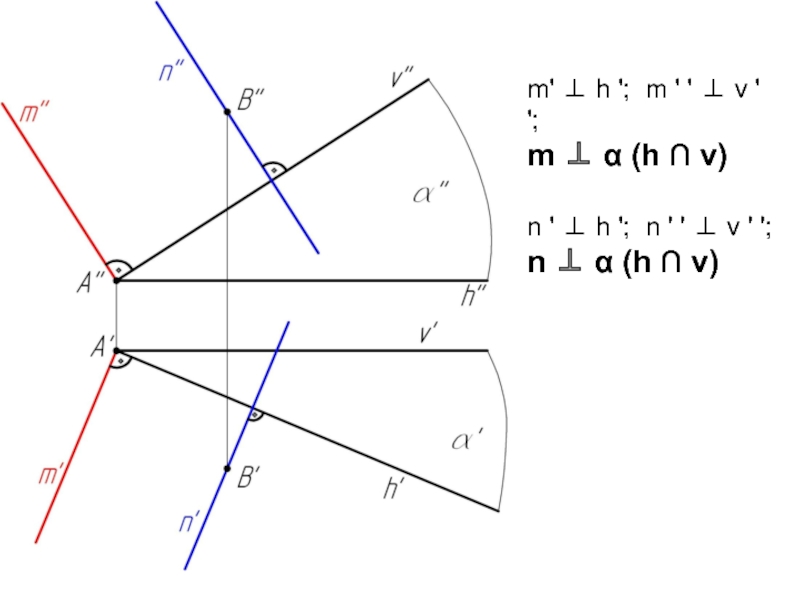
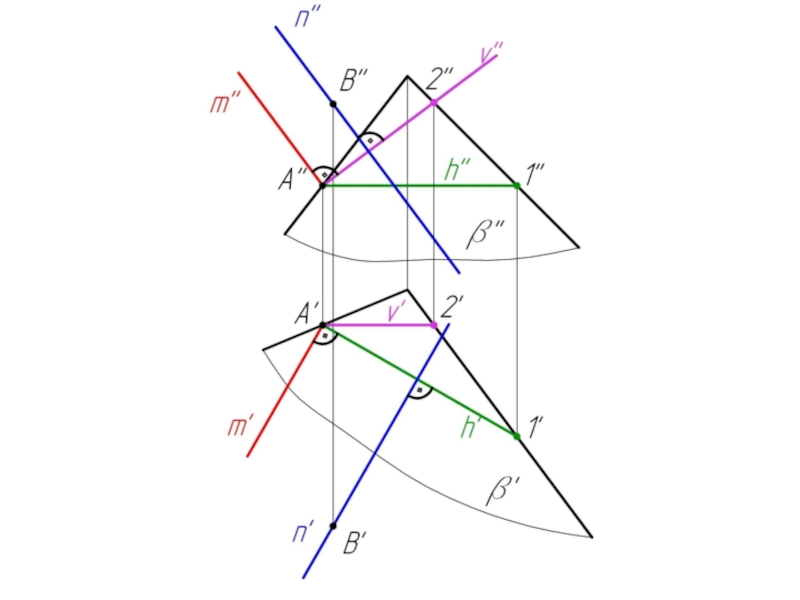
- 34. Пример 1: Из точки А и В провести прямые m и n перпендикулярные плоскости α.
- 35. Чтобы построить прямую, перпендикулярную плоскости, надо иметь
- 37. m' ⊥ h '; m ' '
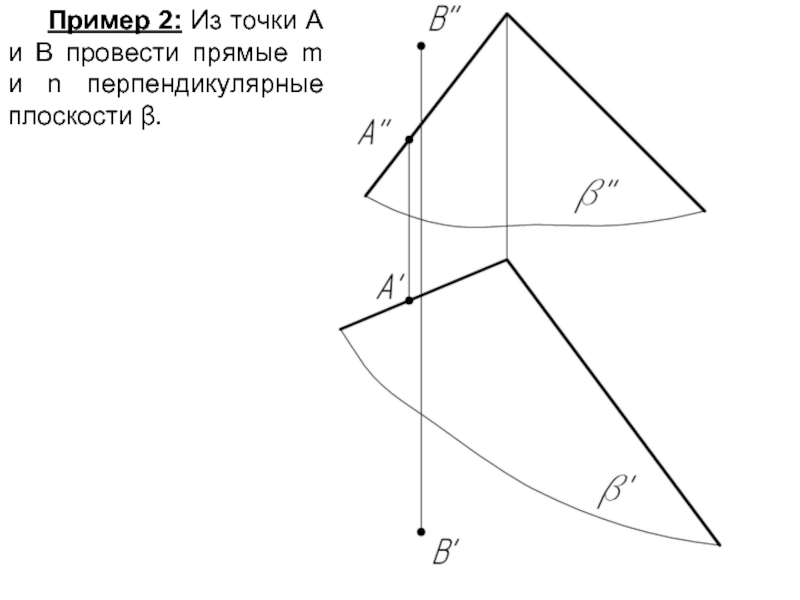
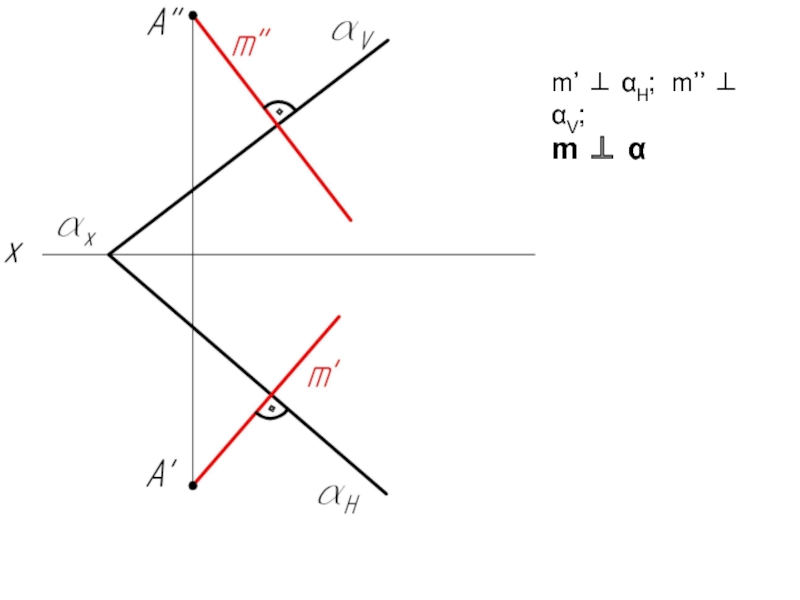
- 38. Пример 2: Из точки А и В провести прямые m и n перпендикулярные плоскости β.
- 42. Если плоскость задана следами, то проекции перпендикуляра перпендикулярны одноименным следам плоскости.
- 43. m’ ⊥ αH; m’’ ⊥ αV; m ⊥ α
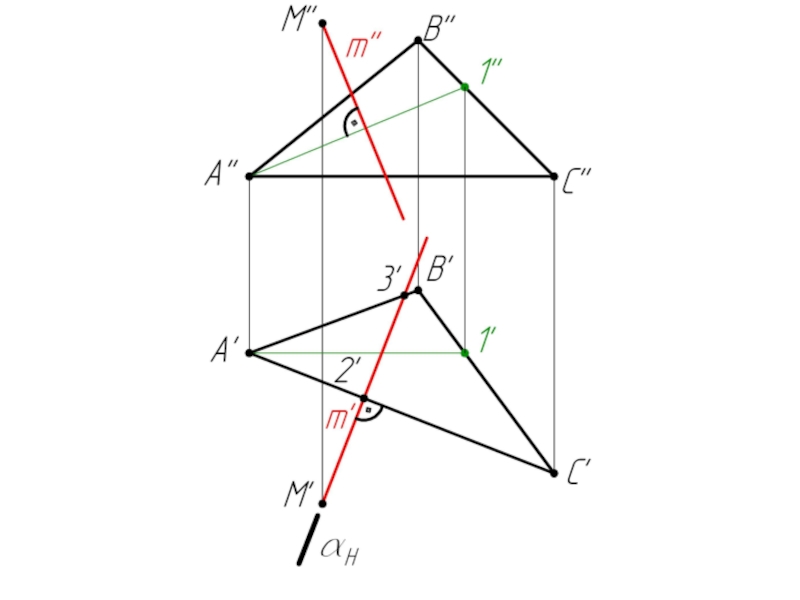
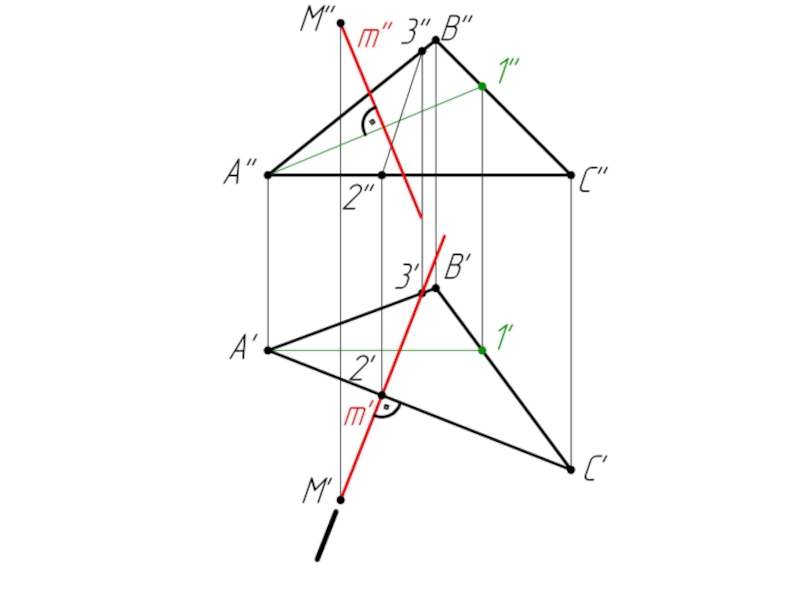
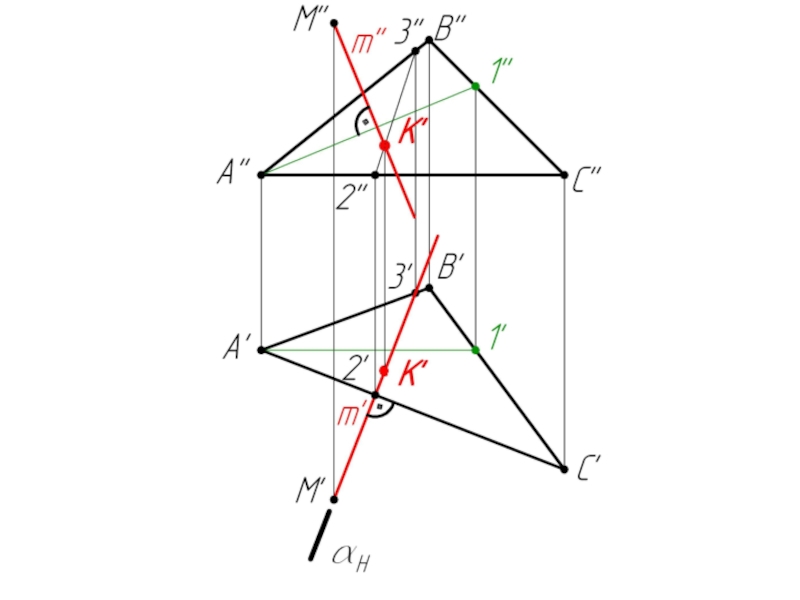
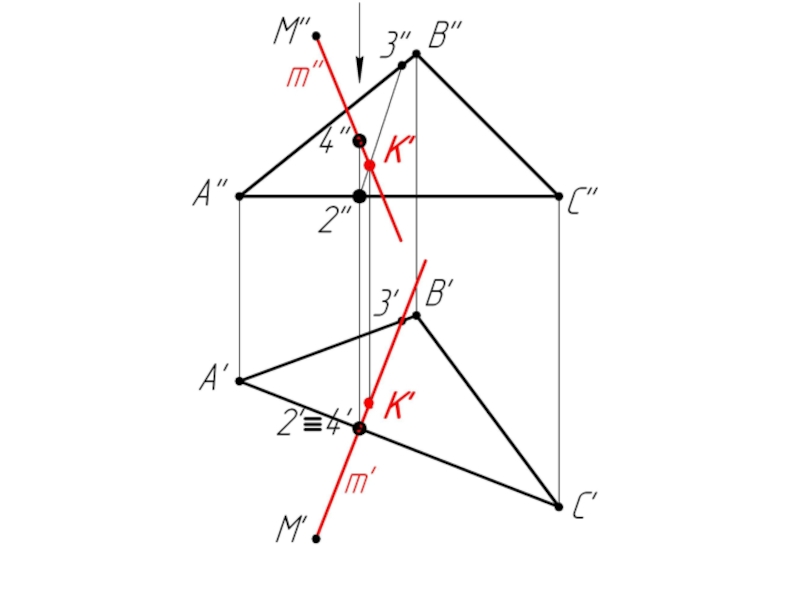
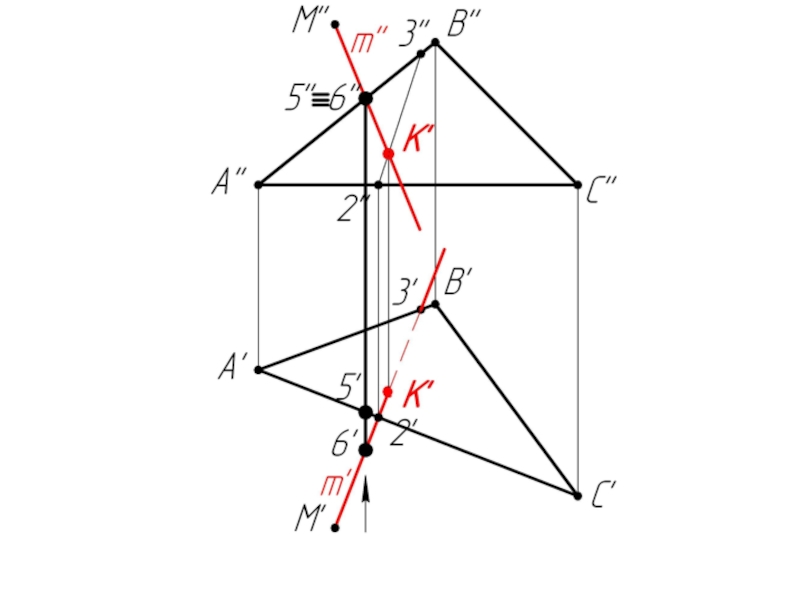
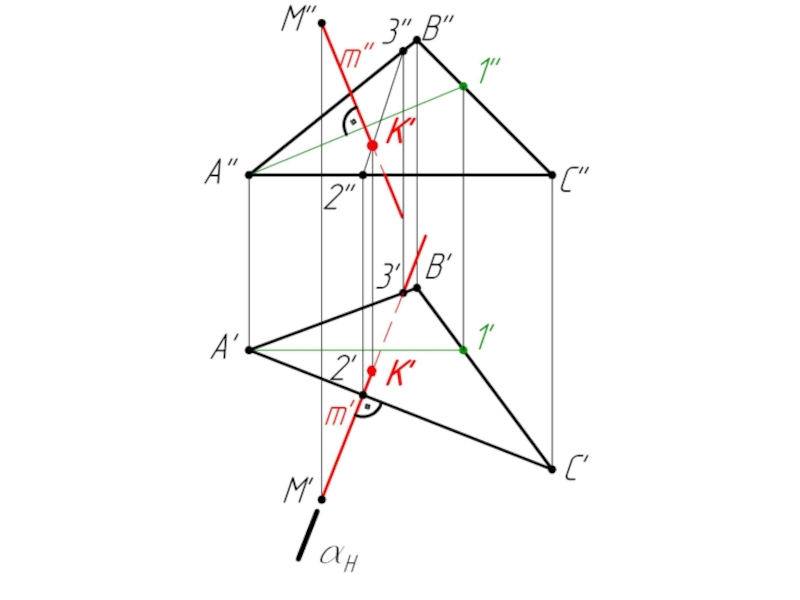
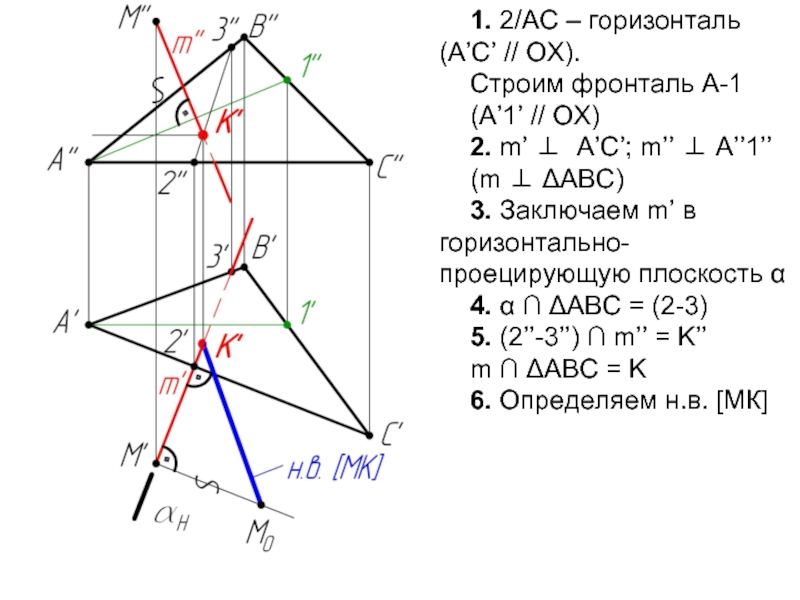
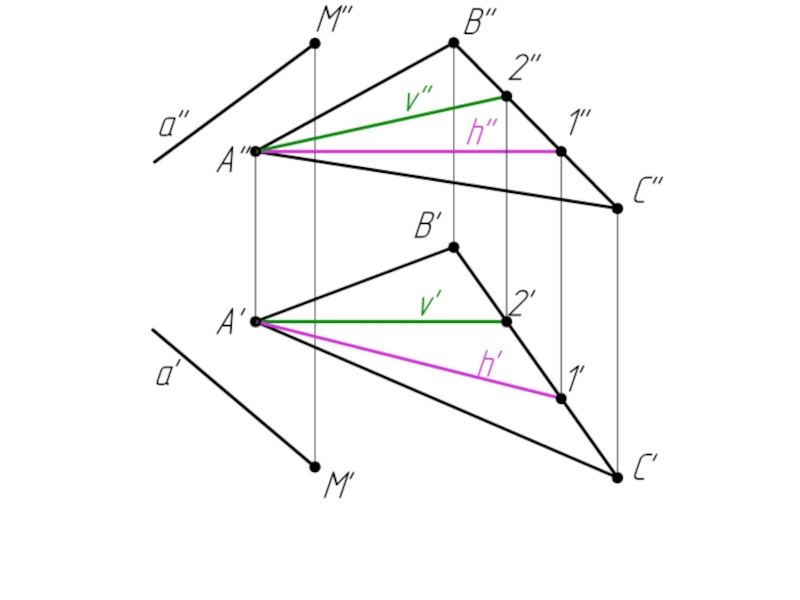
- 44. Пример 3: Определить расстояние от точки М до плоскости ΔАВС.
- 54. 1. 2/АС – горизонталь (A’C’
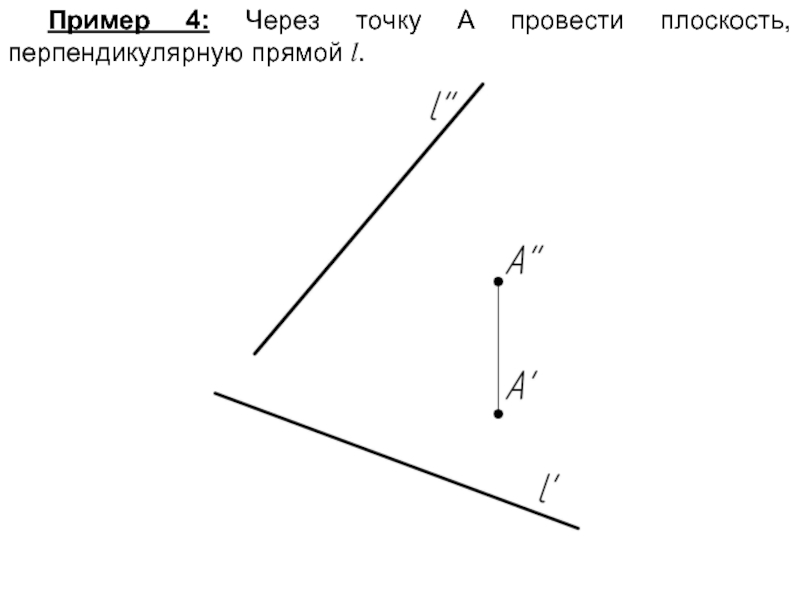
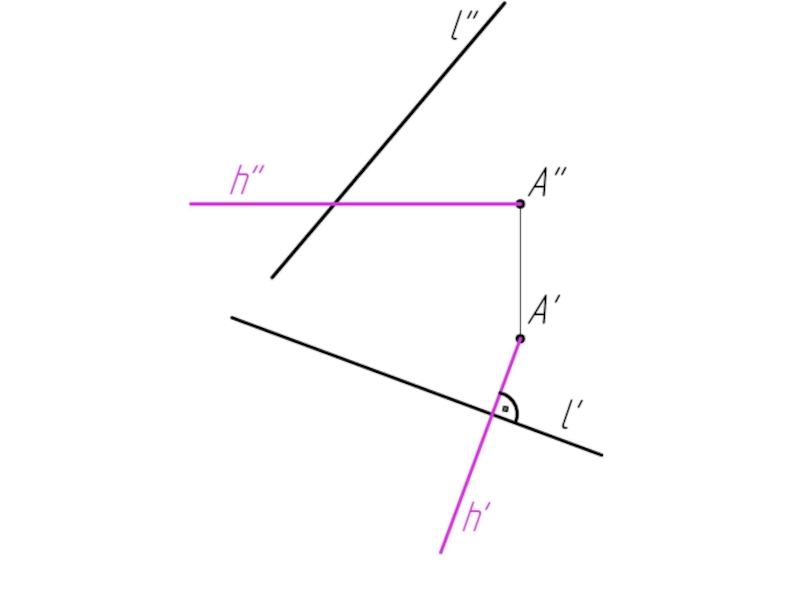
- 55. Пример 4: Через точку А провести плоскость, перпендикулярную прямой l.
- 59. 5.4. Перпендикулярность двух прямых в общем
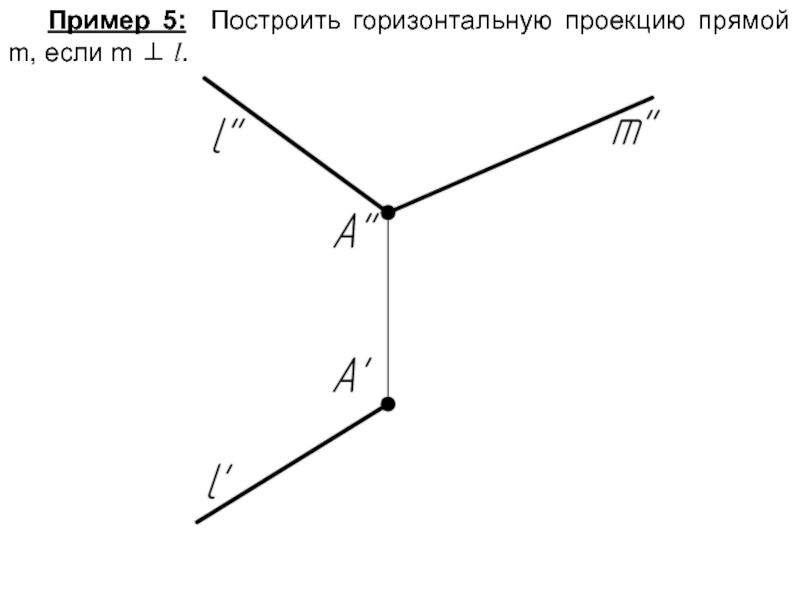
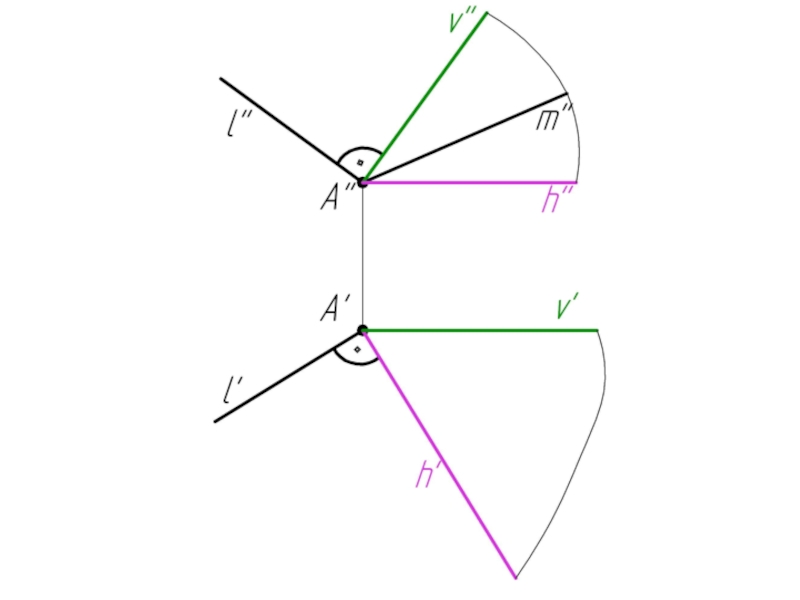
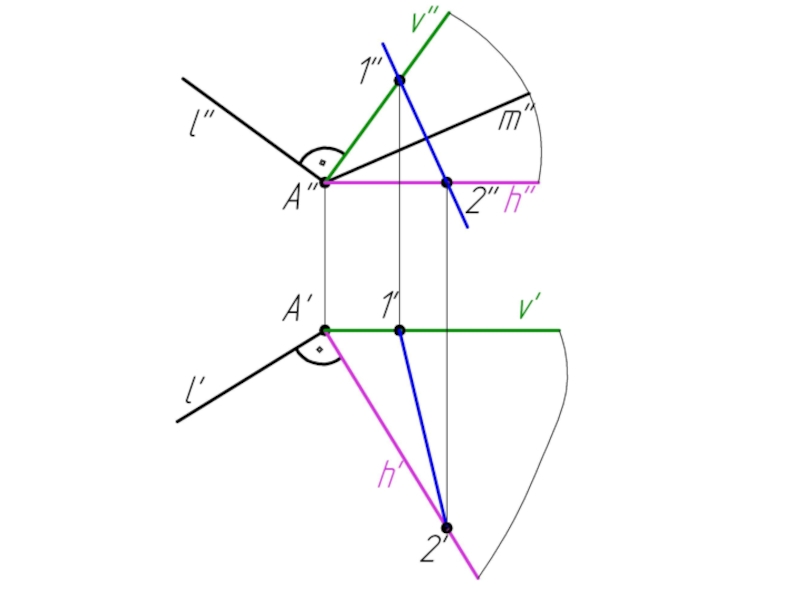
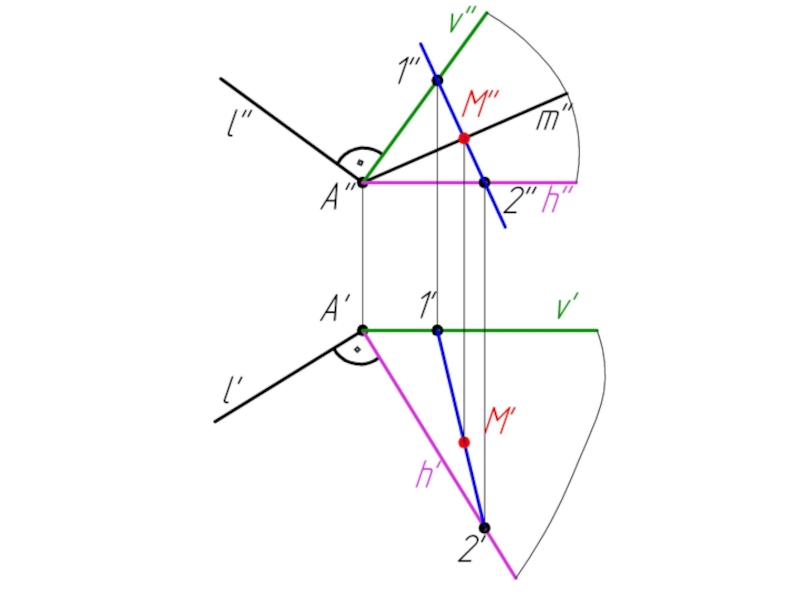
- 60. Пример 5: Построить горизонтальную проекцию прямой m, если m ⊥ l.
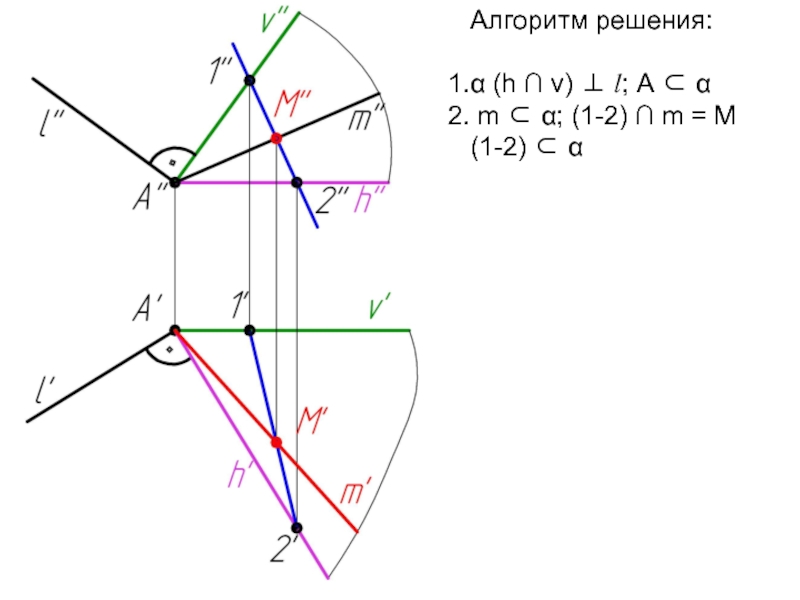
- 64. Алгоритм решения: α (h ∩ v)
- 65. 5.5. Перпендикулярность двух плоскостей Две плоскости
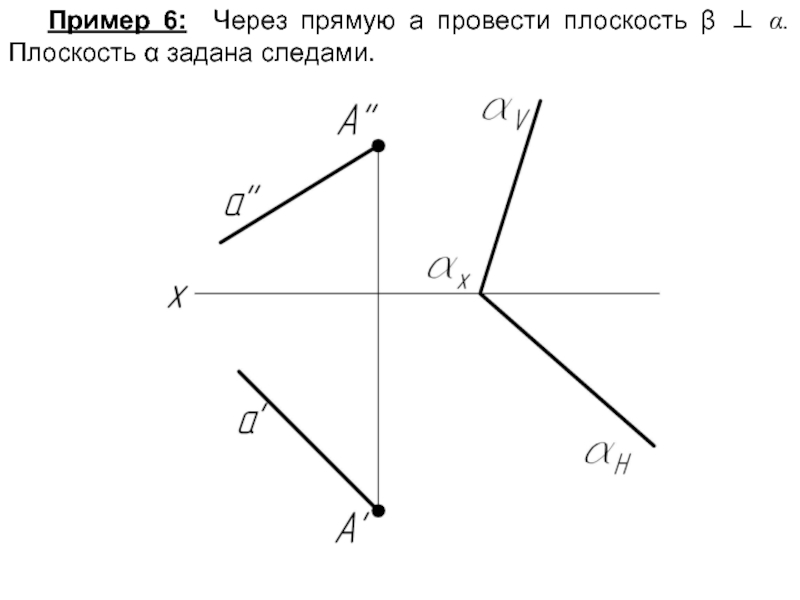
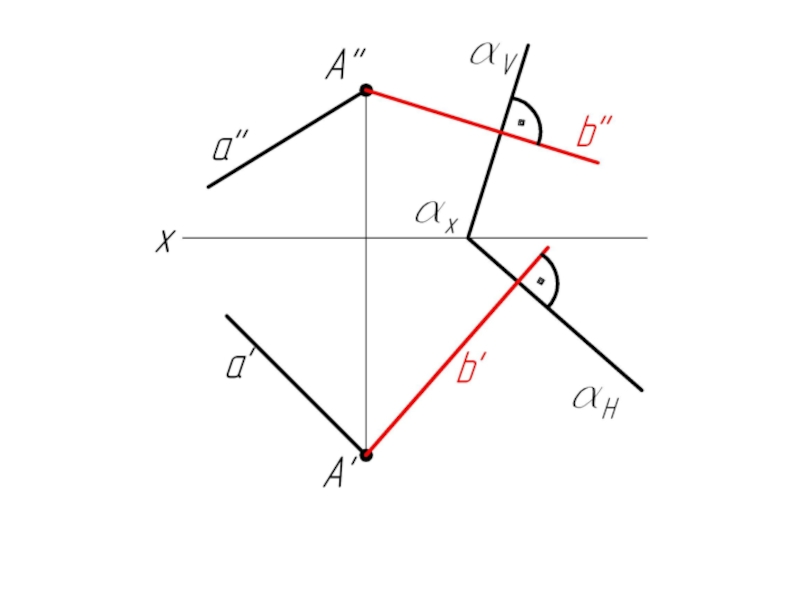
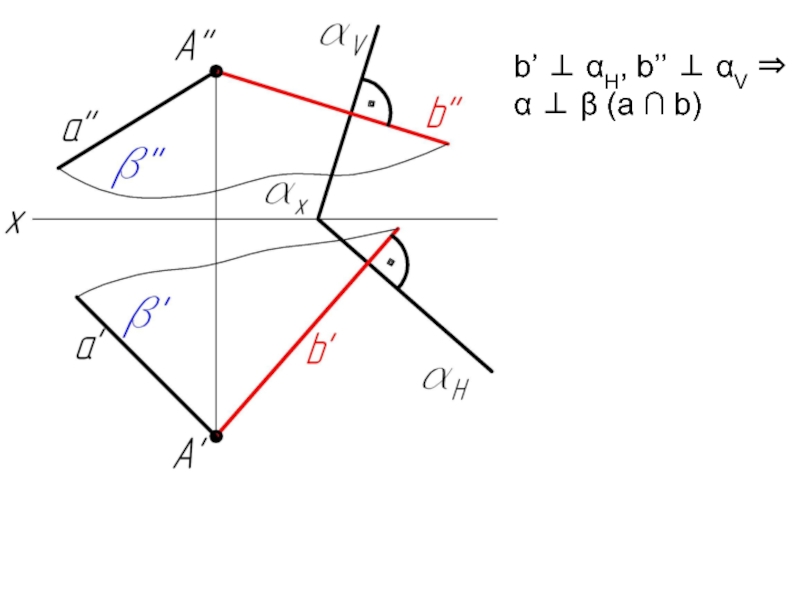
- 66. Пример 6: Через прямую а провести плоскость β ⊥ α. Плоскость α задана следами.
- 68. b’ ⊥ αH, b’’ ⊥ αV ⇒ α ⊥ β (a ∩ b)
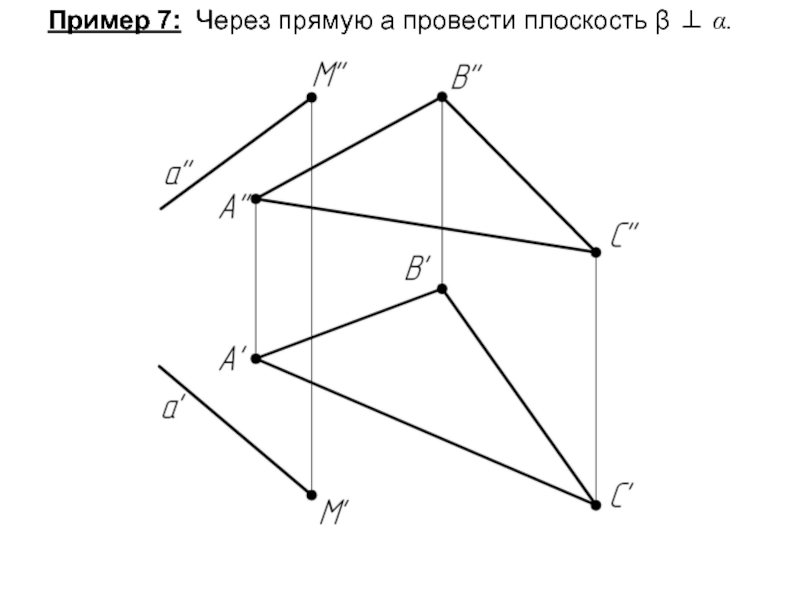
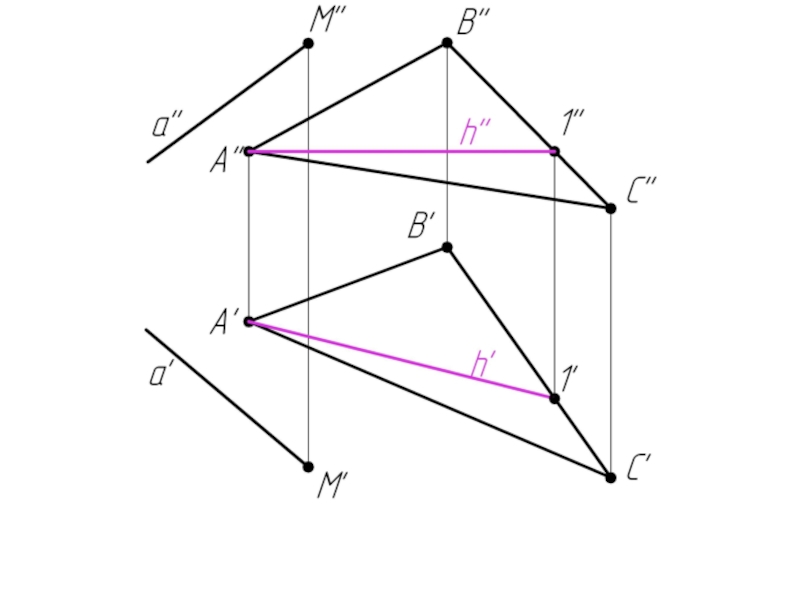
- 69. Пример 7: Через прямую а провести плоскость β ⊥ α.
- 73. Две плоскости, заданные следами, перпендикулярны, если перпендикулярна одна пара следов. α ⊥ β
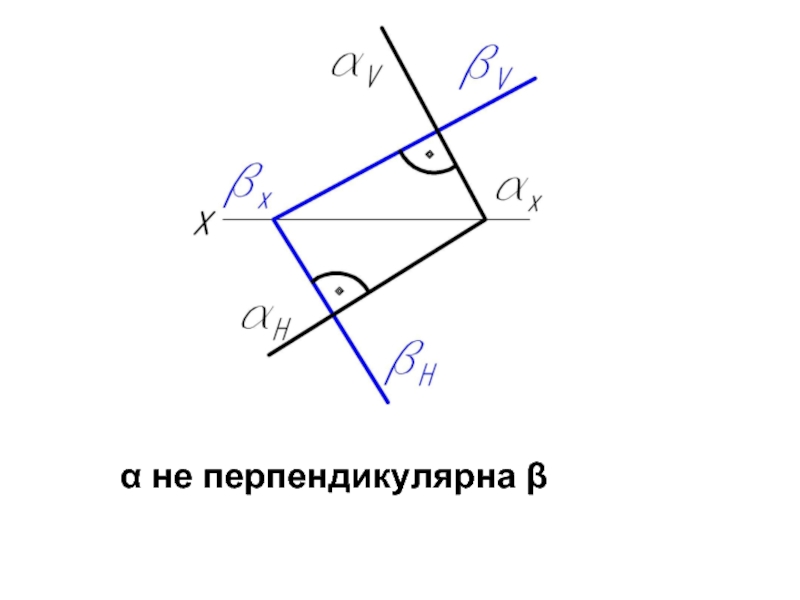
- 74. α не перпендикулярна β
Слайд 2 5.1. Параллельность прямой и плоскости; двух плоскостей.
Прямая параллельна плоскости,
если она параллельна прямой, принадлежащей плоскости.
Плоскость параллельна прямой, если она проходит через прямую параллельную данной прямой.
Плоскость параллельна прямой, если она проходит через прямую параллельную данной прямой.
Слайд 13Две плоскости параллельны, если две пересекающиеся прямые одной плоскости соответственно параллельны
двум пересекающимся прямым другой плоскости.
Если плоскости заданы следами, то одноименные следы параллельных плоскостей параллельны.
Если плоскости заданы следами, то одноименные следы параллельных плоскостей параллельны.
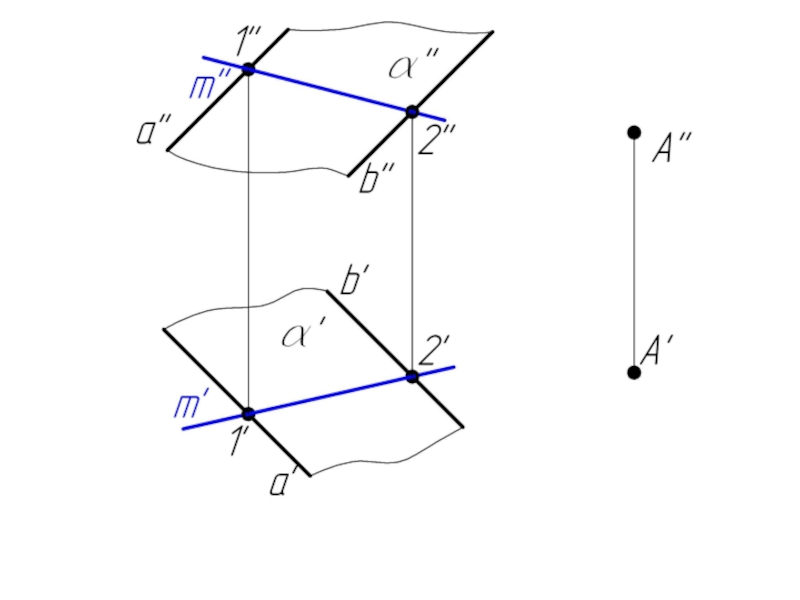
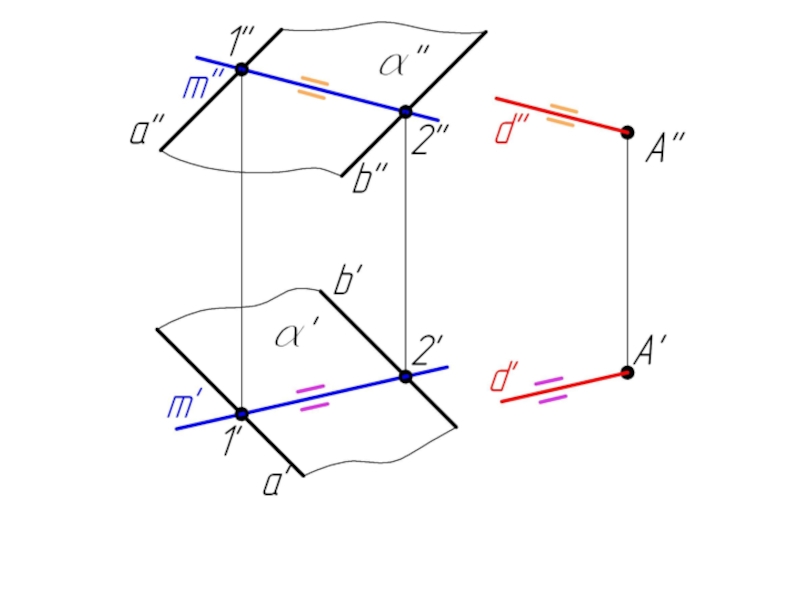
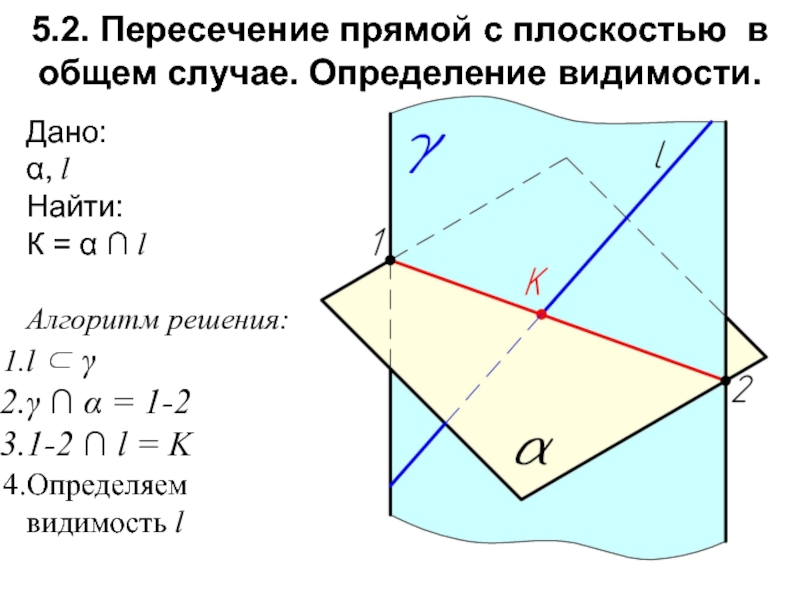
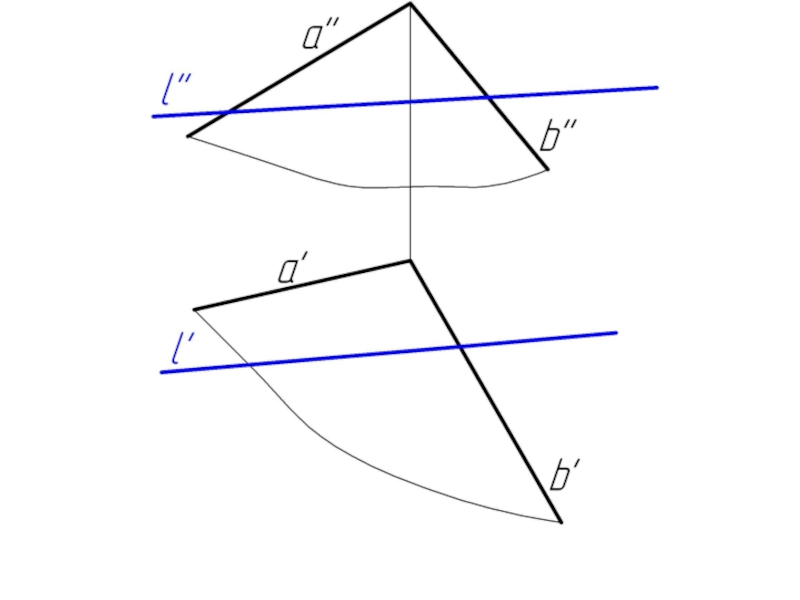
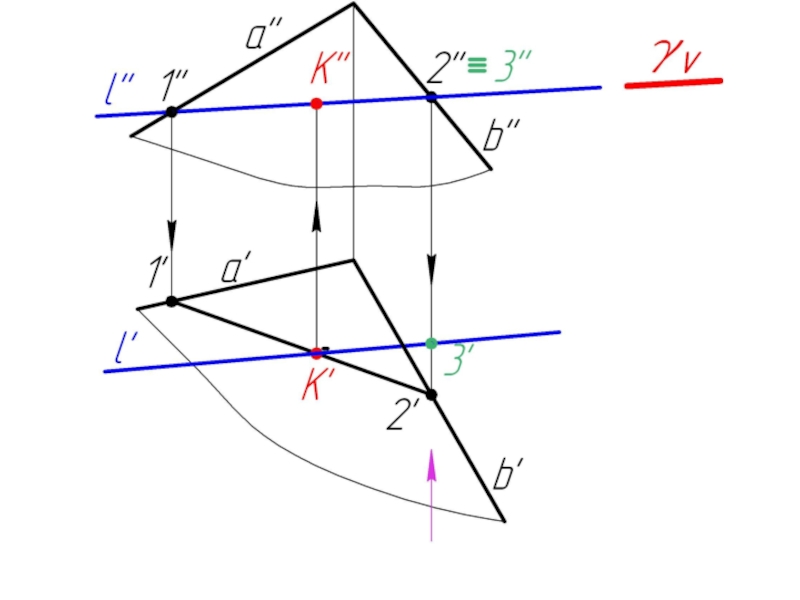
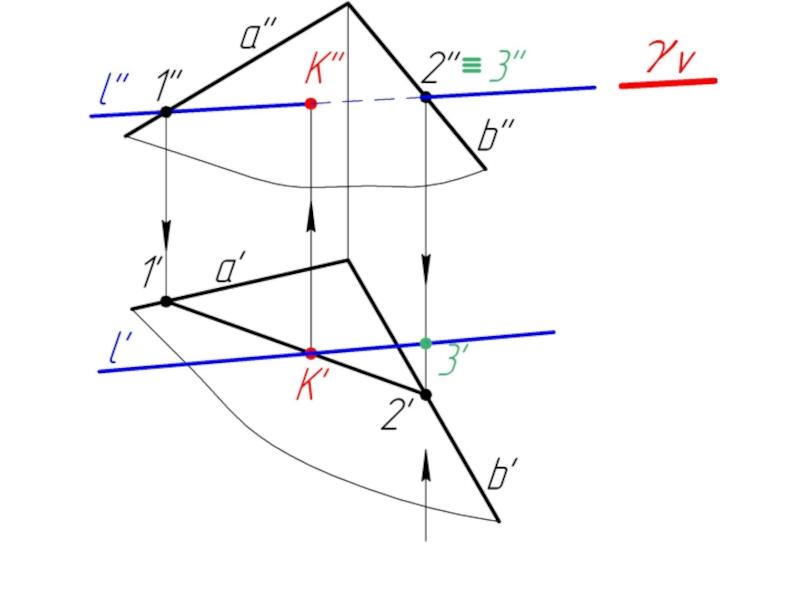
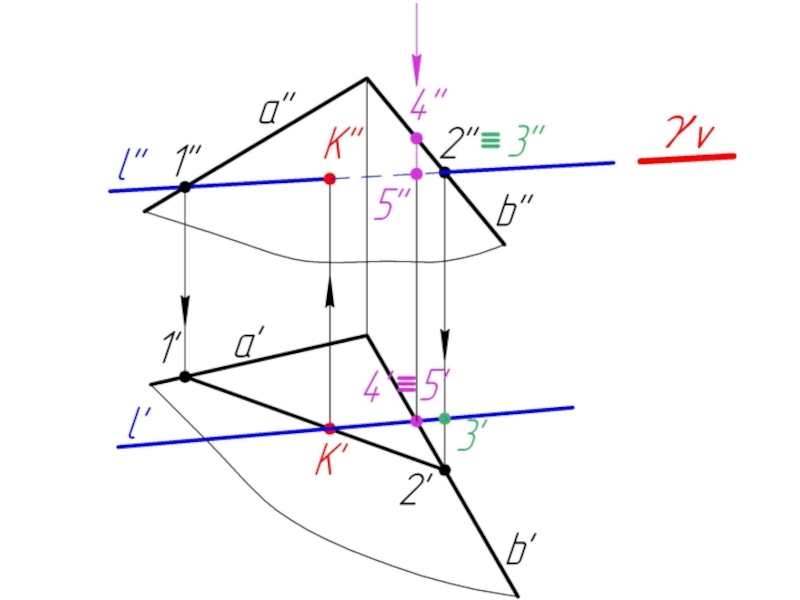
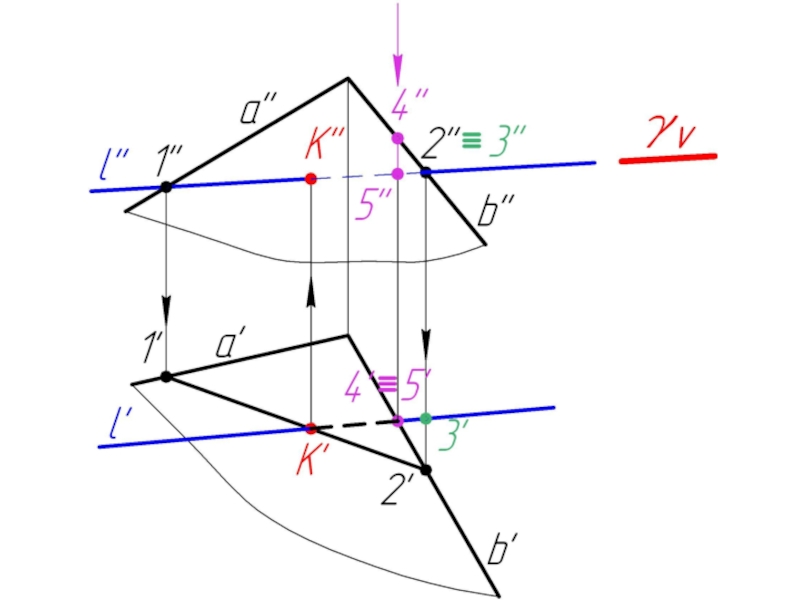
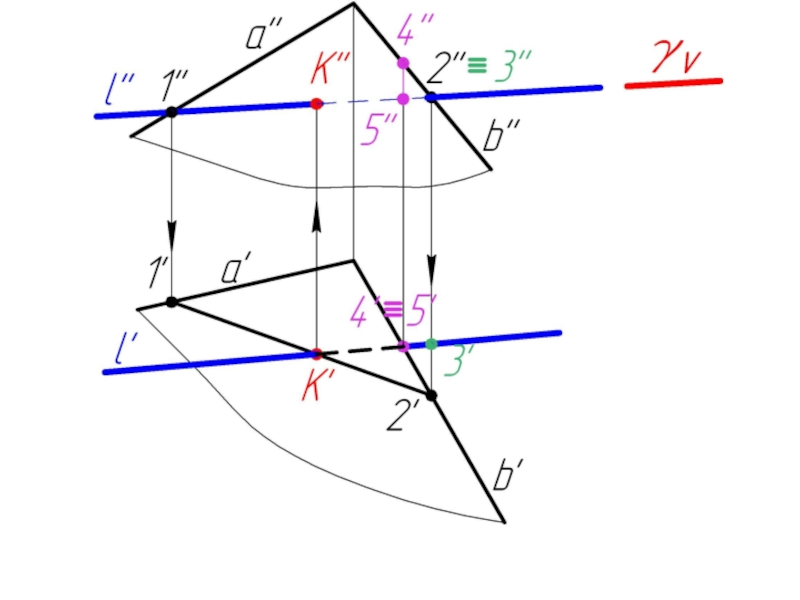
Слайд 235.2. Пересечение прямой с плоскостью в общем случае. Определение видимости.
Дано:
α,
l
Найти:
К = α ∩ l
Алгоритм решения:
l ⊂ γ
γ ∩ α = 1-2
1-2 ∩ l = K
Определяем видимость l
Найти:
К = α ∩ l
Алгоритм решения:
l ⊂ γ
γ ∩ α = 1-2
1-2 ∩ l = K
Определяем видимость l
Слайд 33 5.3. Перпендикулярность прямой и плоскости
Прямая перпендикулярна плоскости, если она
перпендикулярна к двум пересекающимся прямым этой плоскости.
Слайд 35Чтобы построить прямую, перпендикулярную плоскости, надо иметь на чертеже (или построить)
горизонталь и фронталь этой плоскости. Тогда горизонтальная проекция перпендикуляра будет перпендикулярна горизонтали, а фронтальная проекция перпендикуляра будет перпендикулярна фронтали.
Слайд 42Если плоскость задана следами, то проекции перпендикуляра перпендикулярны одноименным следам плоскости.
Слайд 541. 2/АС – горизонталь (A’C’ // OX).
Строим фронталь А-1
(А’1’ // OX)
2. m’ ⊥ A’C’; m’’ ⊥ A’’1’’
(m ⊥ ΔABC)
3. Заключаем m’ в горизонтально-проецирующую плоскость α
4. α ∩ ΔABC = (2-3)
5. (2’’-3’’) ∩ m’’ = K’’
m ∩ ΔABC = K
6. Определяем н.в. [МК]
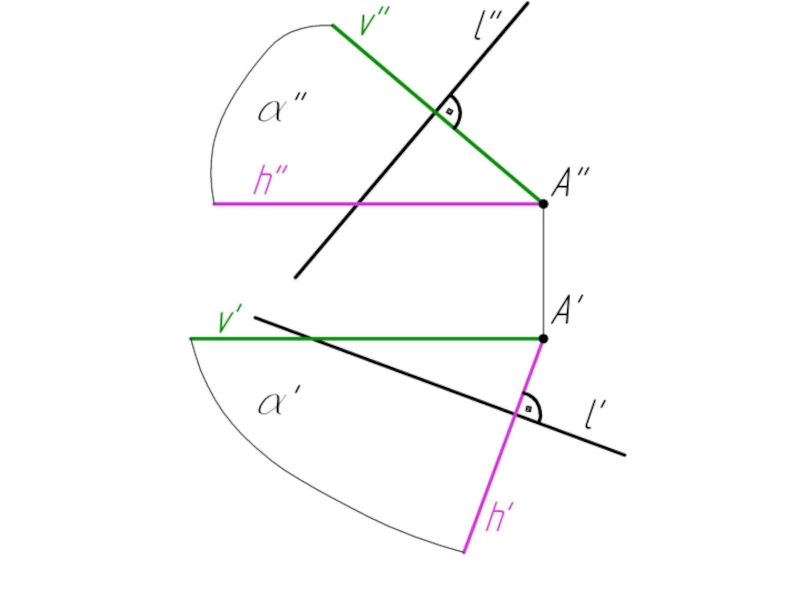
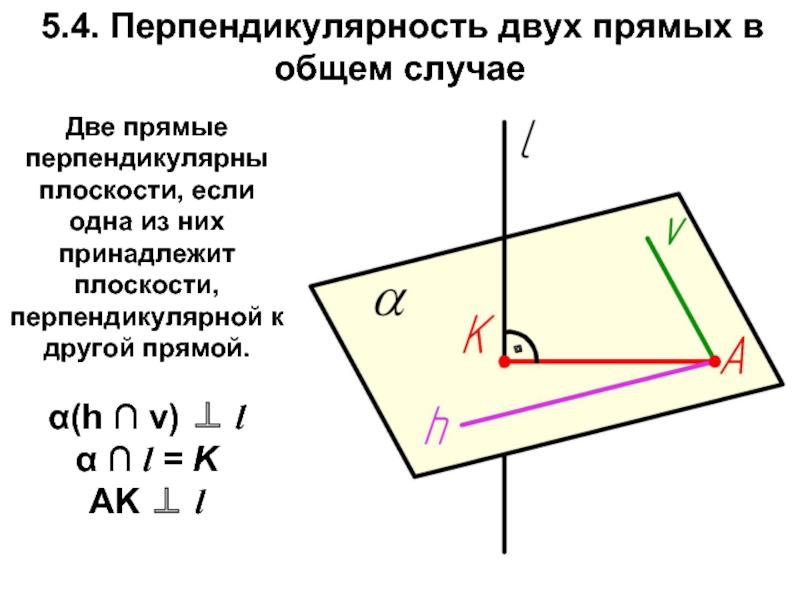
Слайд 59 5.4. Перпендикулярность двух прямых в общем случае
Две прямые перпендикулярны плоскости,
если одна из них принадлежит плоскости, перпендикулярной к другой прямой.
α(h ∩ v) ⊥ l
α ∩ l = K
AK ⊥ l
α(h ∩ v) ⊥ l
α ∩ l = K
AK ⊥ l
Слайд 65 5.5. Перпендикулярность двух плоскостей
Две плоскости перпендикулярны, если она из них
проходит через прямую, перпендикулярную к другой плоскости.
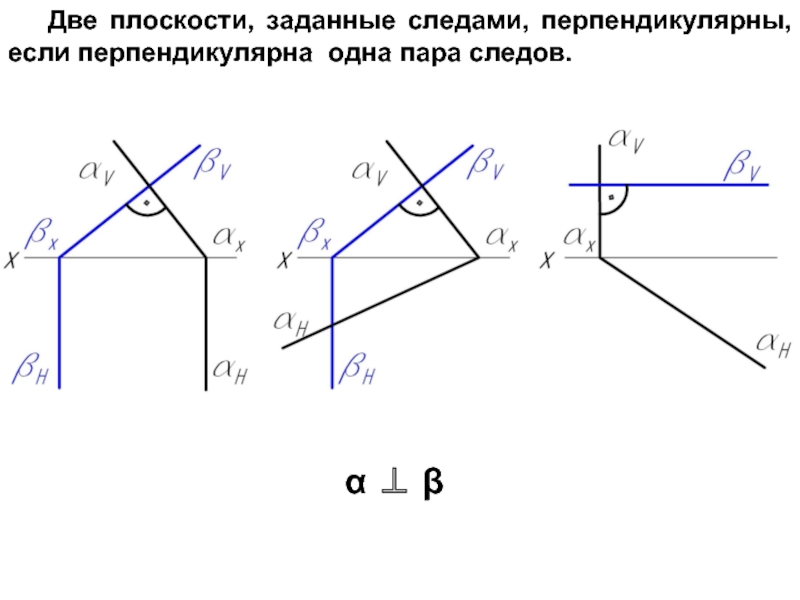
Слайд 73Две плоскости, заданные следами, перпендикулярны, если перпендикулярна одна пара следов.
α
⊥ β