- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Интерполирование и экстраполирование функции презентация
Содержание
- 1. Интерполирование и экстраполирование функции
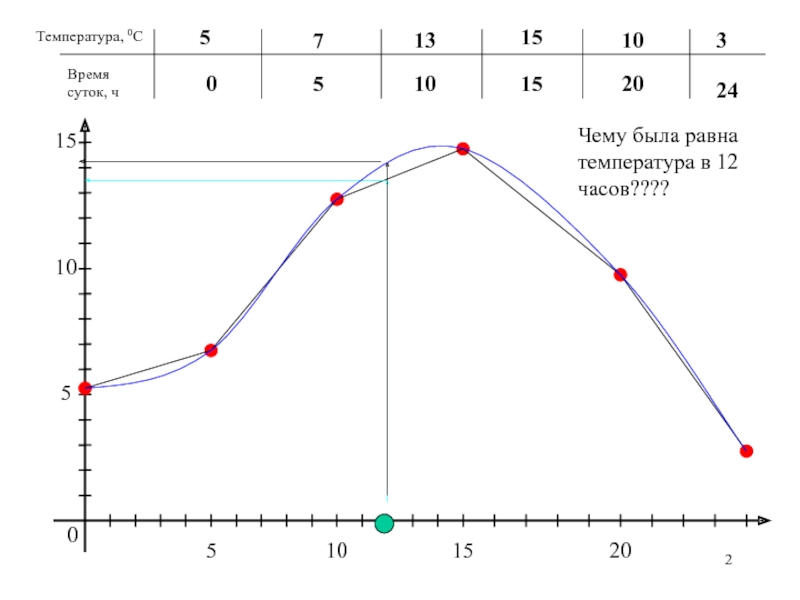
- 2. Температура, 0С Время суток, ч 0 5
- 3. Основные виды интерполяции, экстраполяция и аппроксимация линейная
- 4. Пусть на отрезке [а, b] задана функция
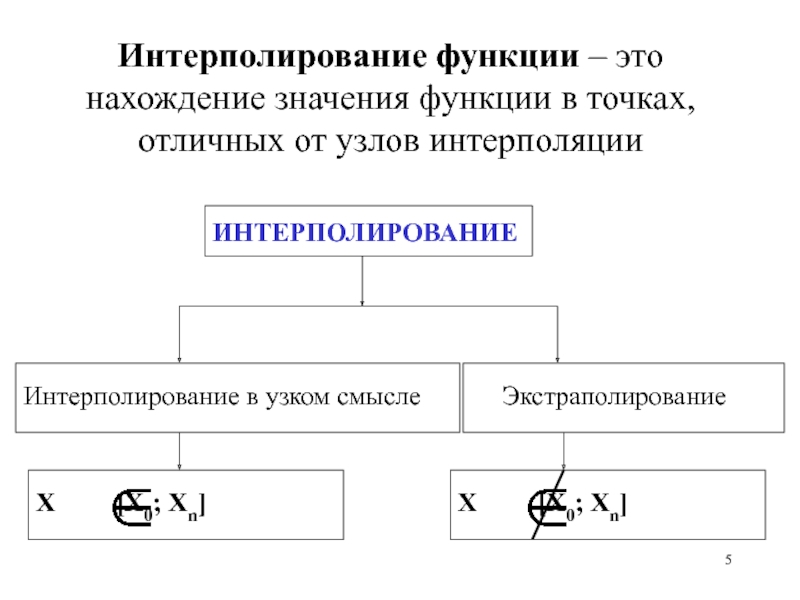
- 5. Интерполирование функции – это нахождение значения функции в точках, отличных от узлов интерполяции
- 6. Fn(х0) = y0, Fn(х1) = y1, …, Fn(хn) = yn Fn(х) - интерполяционный многочлен
- 7. При интерполировании функцию, заданную ее значениями в
- 8. Задача: y0 = f(x0), у1 = f(x1),
- 9. 1) Узлы интерполяции неравноотстоящие h=xi-xi+1 const
- 11. Сокращенный вид интерполяционного многочлена Лагранжа
- 12. Пример 1. Функция задана таблично Пользуясь
- 13. 2) Узлы интерполяции равноотстоящие h=xi-xi+1 =const Пусть q=(x-x0)/h
- 14. Оценка погрешности интерполяционного многочлена Лагранжа
- 15. Интерполяционная формула Ньютона
- 16. Понятие конечных разностей Пусть задана функция y=f(x)
- 17. Понятие конечных разностей Конечные разности первого порядка
- 18. Понятие конечных разностей Конечные разности функций удобно
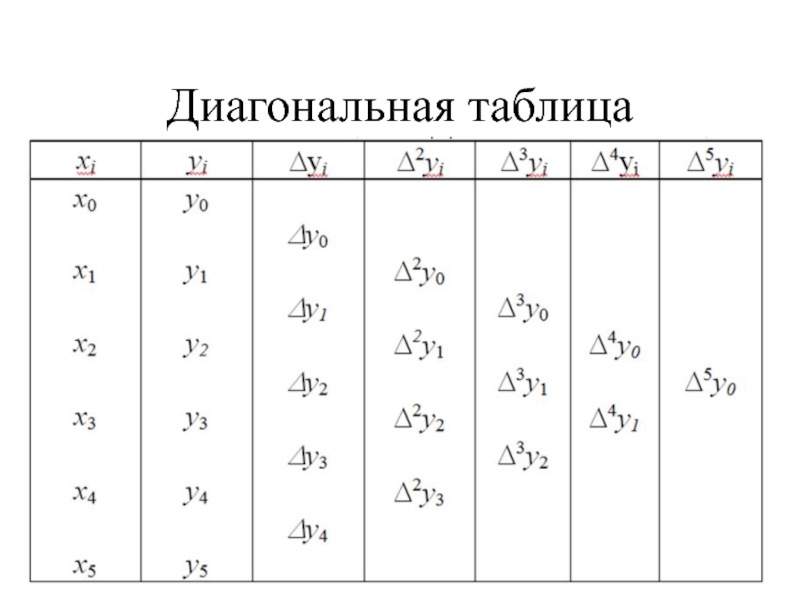
- 19. Диагональная таблица
- 20. Горизонтальная таблица
- 21. Пример 1. Составить таблицу конечных разностей возможных
- 22. Первая интерполяционная формула Ньютона Пусть для функции
- 23. Задача построения многочлена сводится к определению коэффициентов
- 24. Определение коэффициентов Полагаем в интерполирующий полиноме
- 25. Определение коэффициентов Для определения а2 составим конечную
- 26. Построение многочлена Аналогично можно найти другие коэффициенты.
- 27. Первая интерполяционная формула Ньютона
- 28. Первая интерполяционная формула Ньютона Для практического использования
- 29. Пример Дана таблица значений теплоёмкости вещества в
- 30. Пример 1. Функция задана своими
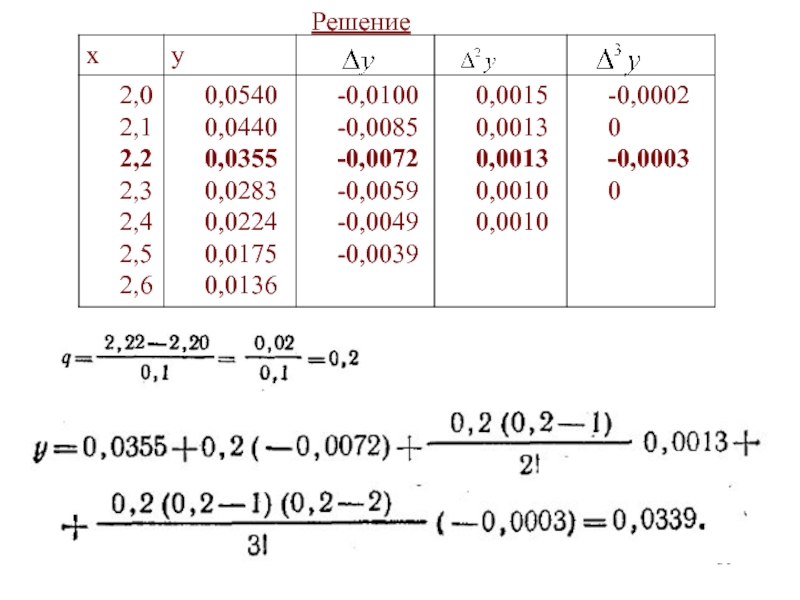
- 31. Решение
- 32. Вторая интерполяционная формула Ньютона Второй интерполяционный полином
- 33. Определение коэффициентов Коэффициенты а0,а1,..., аn определяем
- 34. Определение коэффициентов 2.Полагаем x=xn-1, тогда:
- 35. Определение коэффициентов Аналогично можно найти другие коэффициенты многочлена:
- 36. Вторая интерполяционная формула Ньютона Подставляя эти выражения
- 37. Вторая интерполяционная формула Ньютона Введем обозначения:
- 38. Вторая интерполяционная формула Ньютона Произведя замену ,
- 39. Пример
- 40. Пример
- 41. Аппроксимация функций Особенностью интерполяции являлось то, что
- 42. Особенности аппроксимации если для описания табличных данных будет выбрана функция с меньшим количеством коэффициентов (m
- 43. Особенности аппроксимации В лучшем случае, она будет
- 44. Условия применения аппроксимации Когда количество табличных значений
- 45. Условия применения аппроксимации Когда вид
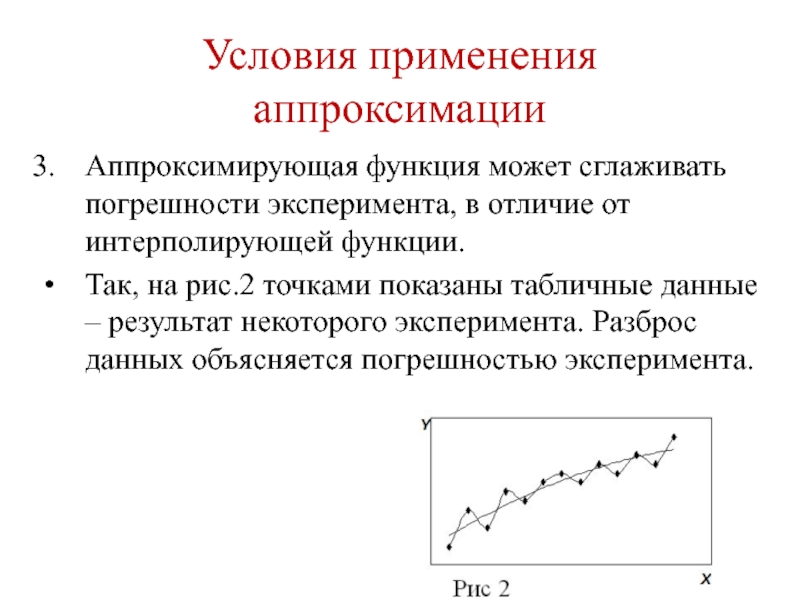
- 46. Условия применения аппроксимации Аппроксимирующая функция может сглаживать
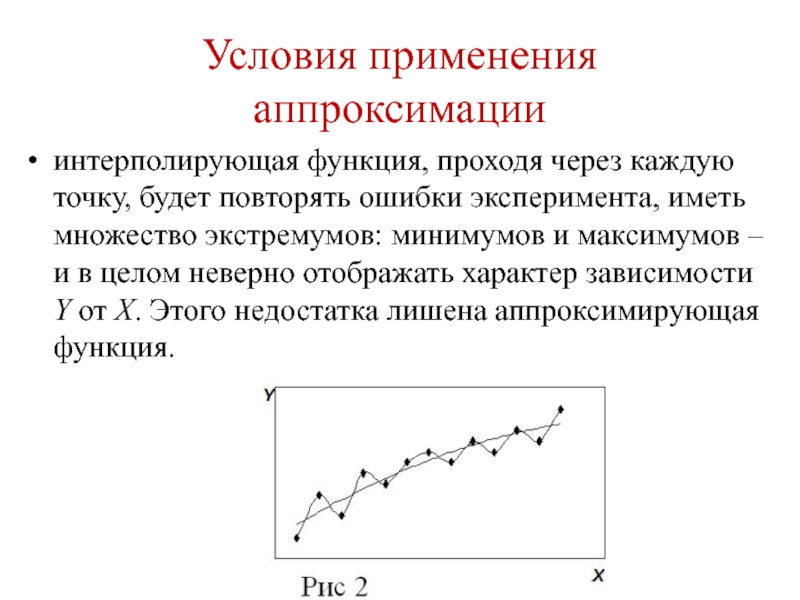
- 47. Условия применения аппроксимации интерполирующая функция, проходя через
- 48. Условия применения аппроксимации Интерполирующей функцией невозможно описать
Слайд 3Основные виды интерполяции, экстраполяция и аппроксимация
линейная интерполяция, при которой промежуточные точки,
квадратичная интерполяция, при которой промежуточные точки между узловыми точками (xi, yi), (xi+1, yi+1) и (xi+2, yi+2) лежат на отрезке параболы, соединяющей эти узловые точки;
полиномиальная интерполяция, при которой промежуточные точки вычисляются как значение некоторого многочлена pn(x), имеющего значения в узловых точках точно совпадающие с fi(xi);
Сплайновая интерполяция, при которой промежуточные точки находятся с помощью отрезков полиномов невысокой степени, проходящих через узловые точки и поддерживающие определенные условия стыковки в концевых точках.
экстраполяция — вычисление функции вне того интервала, на котором она задана в виде таблицы, графически или иным способом.
аппроксимация таблично заданная функция заменяется другой функцией, как правило, более простой и поэтому более быстро вычисляемой.
Слайд 4Пусть на отрезке [а, b] задана функция у = f(x)
y0
х0, х1 ,..., хn - узлы интерполяции
Математическая постановка задач интерполирования
F(х) - табулированная функция
yо = F(х0) = f(xо), y1 = F(х1) = f(x1),..., yn = F(хn) = f(xn)
Слайд 5Интерполирование функции – это нахождение значения функции в точках, отличных от
Слайд 7При интерполировании функцию, заданную ее значениями в узлах интерполяции (то есть,
Интерполирование с помощью многочлена Лагранжа
Интерполирование с помощью многочлена Ньютона
Равноотстоящие узлы интерполяции: h=xi-xi+1=const
Слайд 8Задача:
y0 = f(x0), у1 = f(x1), …, уn = f(xn)
L(x) –
Ln(х0) = y0
Ln(х1) = y1
…
Ln(хn) = yn
Слайд 12Пример 1. Функция задана таблично
Пользуясь интерполяционным
многочленом Лагранжа, найти ее
Решение.
Подставляя в формулу х=4, получим
Слайд 16Понятие конечных разностей
Пусть задана функция y=f(x) на отрезке [x0,xn], который разбит
f(x0)=y0, f(x1)=y1, ..., f(xn)=yn.
Слайд 17Понятие конечных разностей
Конечные разности первого порядка
Δy0 = y1 – y0
Δy1
. . . . .
Δyn-1 = yn – yn-1.
Конечные разности второго порядка
Δ2y0 = Δy1 – Δy0
Δ2y1 = Δy2 – Δy1
. . . . . .
Δ2yn-2 = Δyn-1 – Δyn-2
Аналогично определяются конечные разности высших порядков:
Δky0 = Δk-1y1 – Δk-1y0
Δky1 = Δk-1y2 – Δk-1y1
. . . . . .
Δkyi = Δk-1yi+1 – Δk-1yi , i = 0,1,...,n-k.
Слайд 18Понятие конечных разностей
Конечные разности функций удобно располагать в таблицах, которые могут
Диагональными;
Горизонтальными.
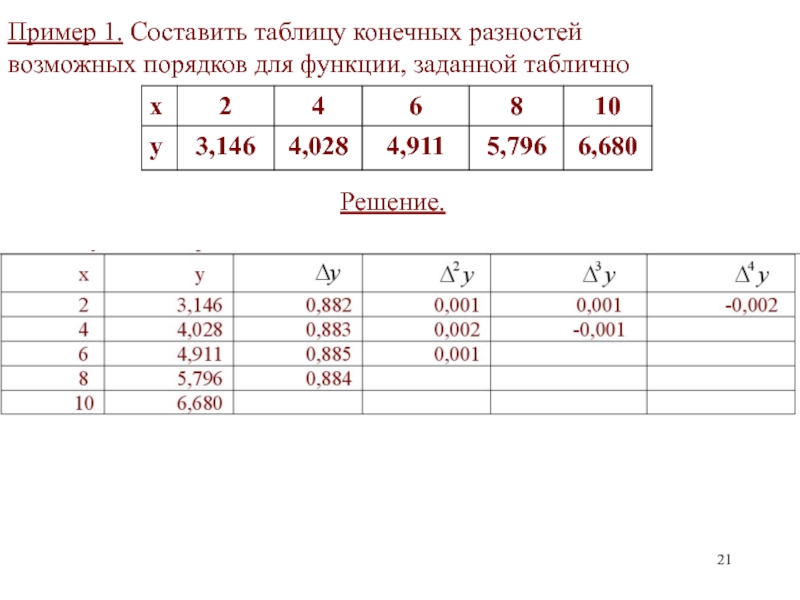
Слайд 21Пример 1. Составить таблицу конечных разностей
возможных порядков для функции, заданной таблично
Решение.
Слайд 22Первая интерполяционная формула Ньютона
Пусть для функции y = f(x) заданы значения
Необходимо найти полином Pn(x) степени не выше n, принимающий в точках (узлах) xi значения:
Pn (xi) = yi , i=0,...,n.
Запишем интерполирующий полином в виде:
Слайд 23Задача построения многочлена сводится к определению коэффициентов аi из условий:
Pn(x1)=y1
. . . .
Pn(xn)=yn
Слайд 24Определение коэффициентов
Полагаем в интерполирующий полиноме x = x0 , тогда,
Pn(x0) = y0 = a0 a0=y0.
Найдем коэффициент а1.
При x = x1 получим:
Слайд 25Определение коэффициентов
Для определения а2 составим конечную разность второго порядка.
При x =
Слайд 26Построение многочлена
Аналогично можно найти другие коэффициенты. Общая формула имеет вид.
Подставляя эти выражения в формулу полинома, получаем:
где xi ,yi – узлы интерполяции; x – текущая переменная; h – разность между двумя узлами интерполяции
h – величина постоянная, т.е. узлы интерполяции равноотстоят друг от друга.
Слайд 27Первая интерполяционная формула Ньютона
Этот многочлен называют интерполяционным полиномом Ньютона для интерполяции
Слайд 28Первая интерполяционная формула Ньютона
Для практического использования этот полином записывают в преобразованном
Эта формула применима для вычисления значений функции для значений аргументов, близких к началу интервала интерполирования.
Слайд 29Пример
Дана таблица значений теплоёмкости вещества в зависимости от температуры Cр =f(T).
Таблица 1
Слайд 30Пример 1. Функция
задана своими значениями
Применяя первую интерполяционную формулу
найти
Слайд 32Вторая интерполяционная формула Ньютона
Второй интерполяционный полином Ньютона применяется для нахождения значений
Запишем интерполяционный многочлен в виде:
Слайд 33Определение коэффициентов
Коэффициенты а0,а1,..., аn определяем из условия:
1.Полагаем в интерполяционном многочлене x = xn,, тогда
Слайд 34Определение коэффициентов
2.Полагаем x=xn-1, тогда:
Pn(xn-1)=yn-1=yn+a1(xn-1 – xn) ,
Следовательно:
3.Полагаем x=xn-2 , тогда
Слайд 36Вторая интерполяционная формула Ньютона
Подставляя эти выражения в формулу (1), получим вторую
Слайд 38Вторая интерполяционная формула Ньютона
Произведя замену , получим
Это вторая формула Ньютона для
Слайд 39
Пример
Вычислить теплоемкость (табл.1) для температуры Т=550 К.
Воспользуемся второй формулой Ньютона и
Слайд 40Пример
Следовательно, значение теплоемкости при температуре 550 К равно:
Ср(550)=97,01 Дж/(моль К).
Слайд 41Аппроксимация функций
Особенностью интерполяции являлось то, что интерполирующая функция строго проходит через
Эта особенность обуславливалась тем, что количество коэффициентов в интерполирующей функции (m) было равно количеству табличных значений (n)
Слайд 42Особенности аппроксимации
если для описания табличных данных будет выбрана функция с меньшим
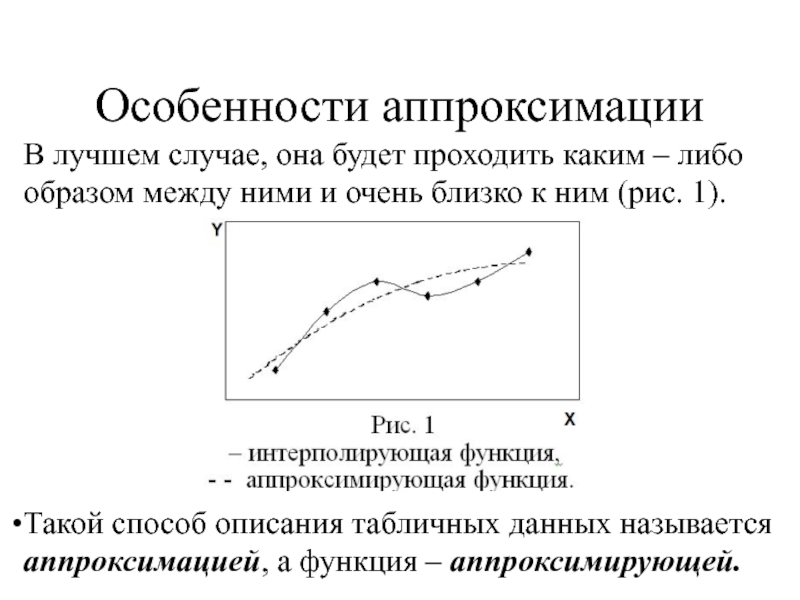
Слайд 43Особенности аппроксимации
В лучшем случае, она будет проходить каким – либо образом
Такой способ описания табличных данных называется аппроксимацией, а функция – аппроксимирующей.
Слайд 44Условия применения аппроксимации
Когда количество табличных значений очень велико. В этом случае
Слайд 45Условия применения аппроксимации
Когда вид функции заранее определен. Такая ситуация возникает, если
Слайд 46Условия применения аппроксимации
Аппроксимирующая функция может сглаживать погрешности эксперимента, в отличие от
Так, на рис.2 точками показаны табличные данные – результат некоторого эксперимента. Разброс данных объясняется погрешностью эксперимента.
Слайд 47Условия применения аппроксимации
интерполирующая функция, проходя через каждую точку, будет повторять ошибки
Слайд 48Условия применения аппроксимации
Интерполирующей функцией невозможно описать табличные данные, в которых есть
Такая ситуация возможна, если один и тот же эксперимент проводится несколько раз при одних и тех же исходных данных. Однако это не является ограничением для использования аппроксимации, где не ставится условие прохождения графика функции через каждую точку.

![Пусть на отрезке [а, b] задана функция у = f(x) y0 = f(x0), у1 =](/img/tmb/5/432152/b2e85505b444566e91b49e6f523f00f2-800x.jpg)




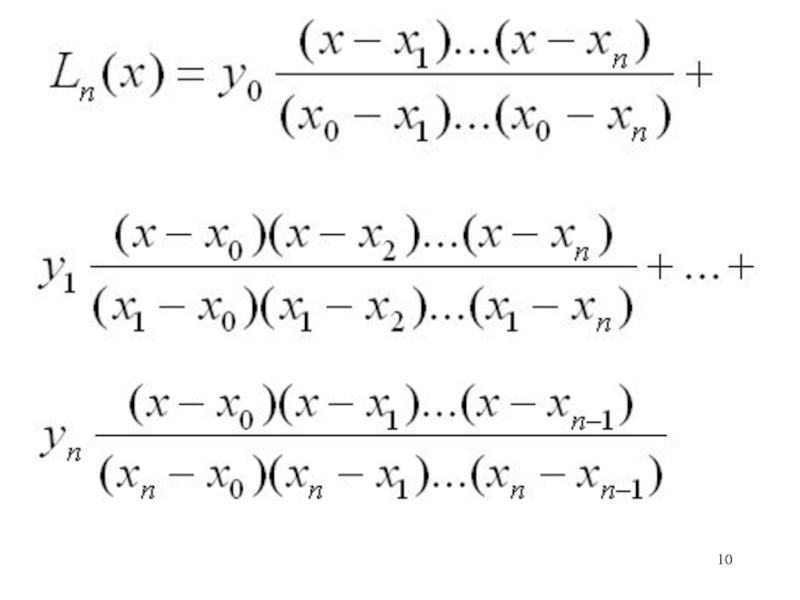





![Понятие конечных разностейПусть задана функция y=f(x) на отрезке [x0,xn], который разбит на n одинаковых отрезков](/img/tmb/5/432152/1b8ee06fae73affdd75f8f38687abf05-800x.jpg)