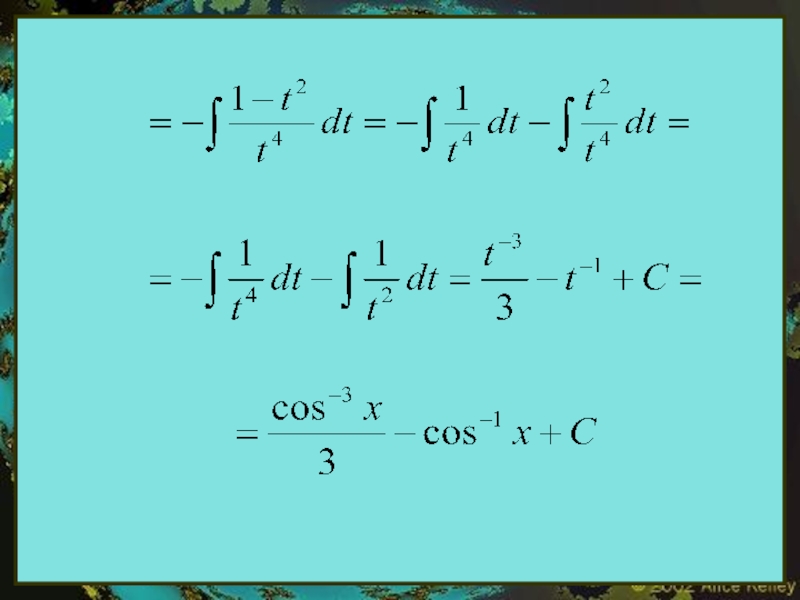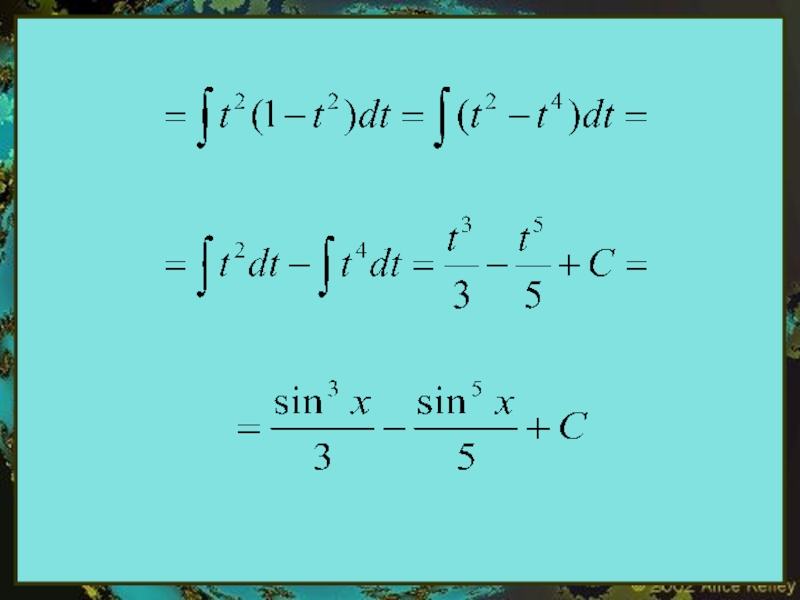- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Интегрирование тригонометрических функций презентация
Содержание
- 1. Интегрирование тригонометрических функций
- 2. Замена переменной: универсальная тригонометрическая подстановка
- 3. Тогда Следовательно
- 4. Пример. Вычислить интеграл:
- 5. Решение:
- 6. 2 Если выражение R(sin x,cos
- 7. Пример. Вычислить интеграл:
- 8. Решение: Следовательно, можно применять рекомендуемую подстановку:
- 10. 3 Если выражение R(sin x,cos
- 11. Пример. Вычислить интеграл:
- 12. Решение: Следовательно, можно применять рекомендуемую подстановку:
- 14. 4 Интегралы вида где α
- 15. Формулы преобразования:
- 16. Пример. Вычислить интеграл:
- 17. Решение:
Слайд 6
2
Если выражение R(sin x,cos x) при замене sin x на (-sin
x) только меняет знак, то интеграл
берется заменой
Слайд 10
3
Если выражение R(sin x,cos x) при замене cos x на (-cos
x) только меняет знак, то интеграл
берется заменой
Слайд 14
4
Интегралы вида
где α и β – действительные числа, вычисляются с помощью
формул, преобразующих произведение тригонометрических функций в сумму.