- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Моделирование многогранников из развёрток (правильные и полуправильные многогранники) презентация
Содержание
- 1. Моделирование многогранников из развёрток (правильные и полуправильные многогранники)
- 2. Многогранник называется правильным если все его грани
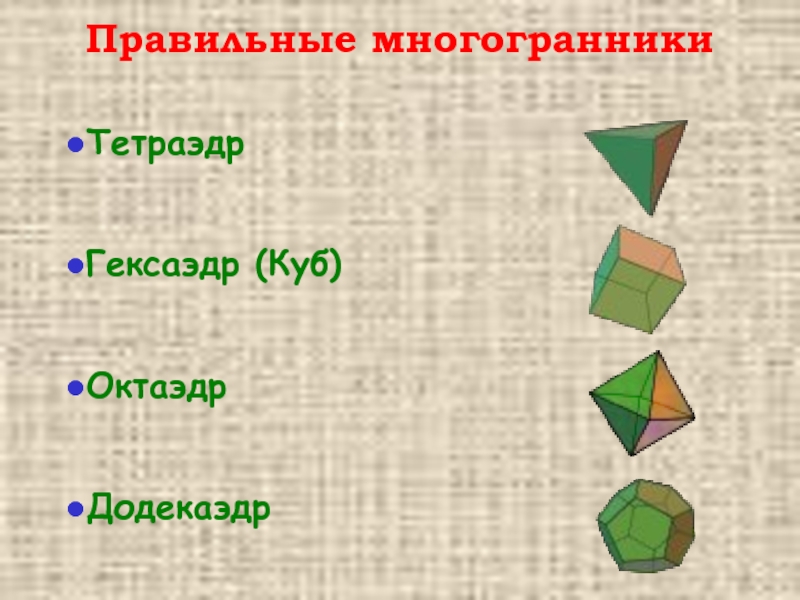
- 3. Тетраэдр Гексаэдр (Куб) Октаэдр Додекаэдр Правильные многогранники
- 4. Икосаэдр Правильные многогранники
- 5. Тетраэдр
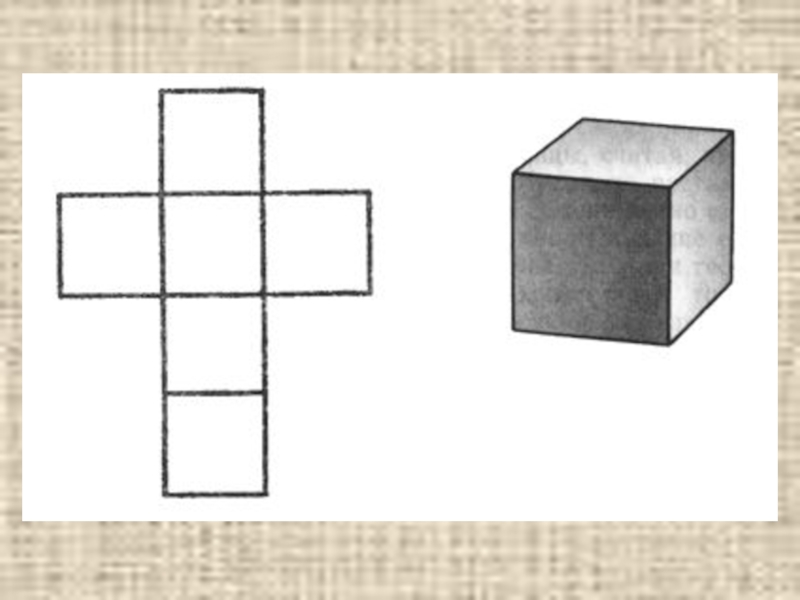
- 7. Куб
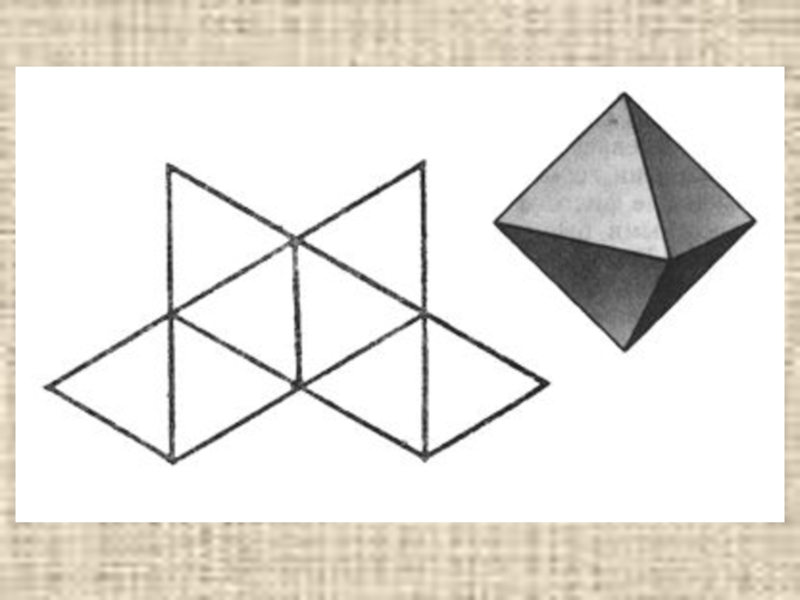
- 9. Октаэдр
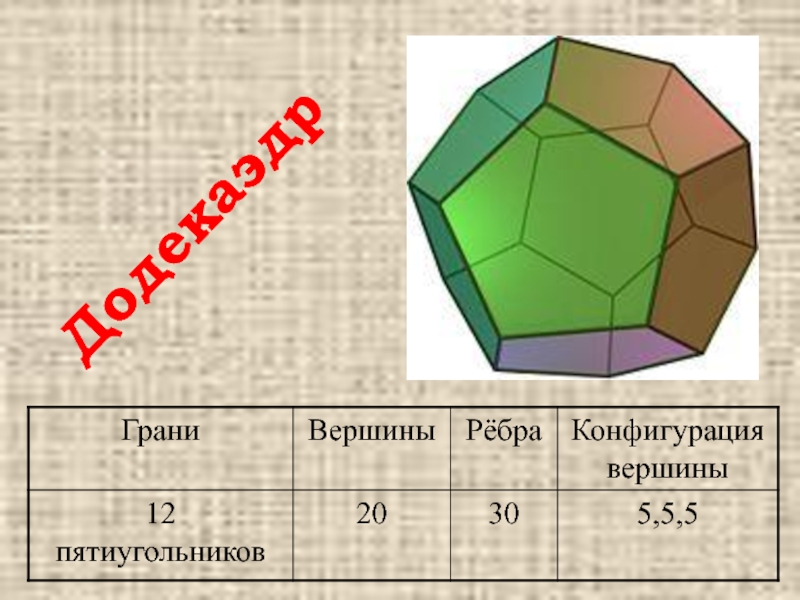
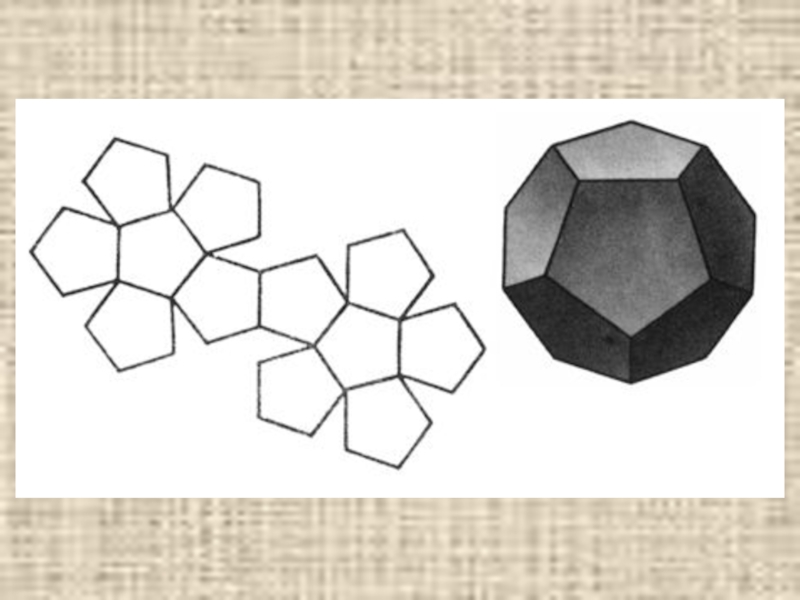
- 11. Додекаэдр
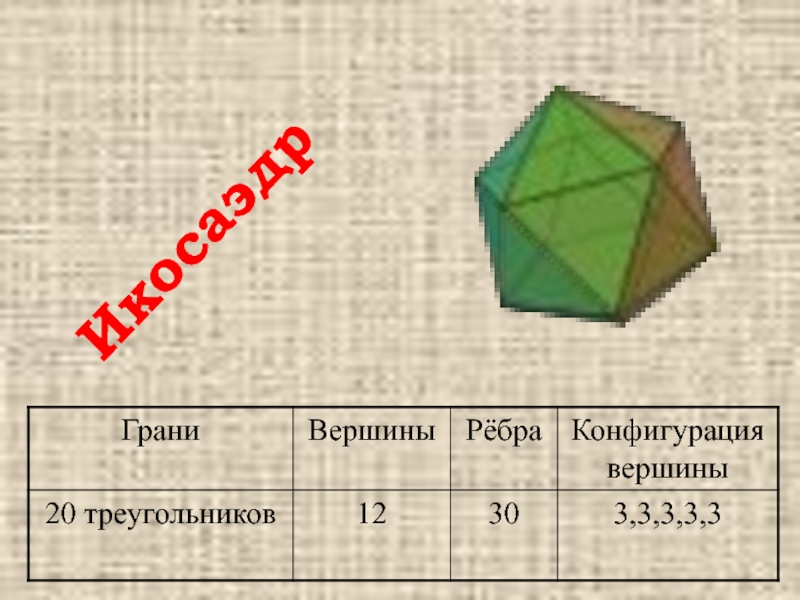
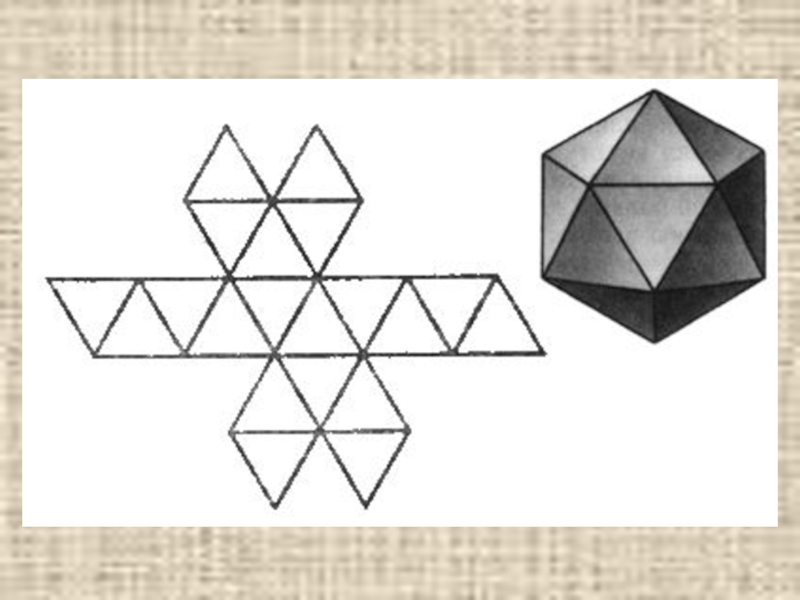
- 13. Икосаэдр
- 15. Многогранник называется равноугольно полуправильным или архимедовым,
- 16. Усеченный тетраэдр Усеченный куб Усеченный октаэдр Усеченный додекаэдр 13 основных полуправильных многогранников
- 17. Усеченный икосаэдр Кубоктаэдр Икосододекаэдр Ромбокубоктаэдр 13 основных полуправильных многогранников
- 18. Ромбоикосододекаэдр Ромбоусечённый кубоктаэдр Ромбоусечённый икосододекаэдр Курносый куб 13 основных полуправильных многогранников
- 19. Курносый додекаэдр 13 основных полуправильных многогранников Ещё один полуправильный многогранник Псевдоромбокубоктаэдр
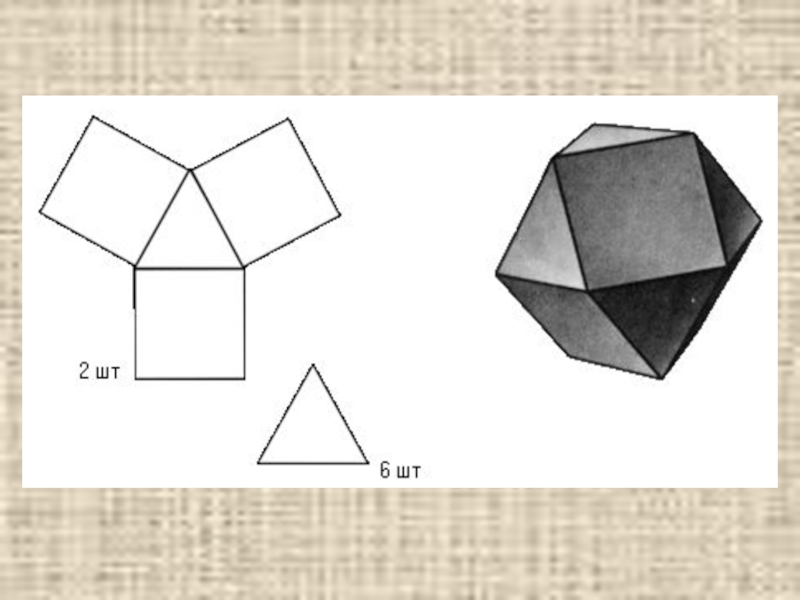
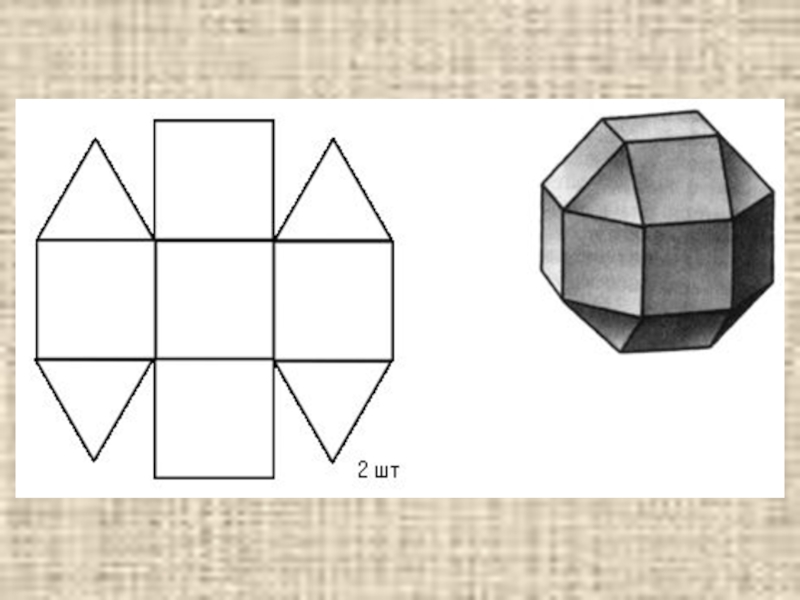
- 20. Кубоктаэдр
- 22. Икосододекаэдр
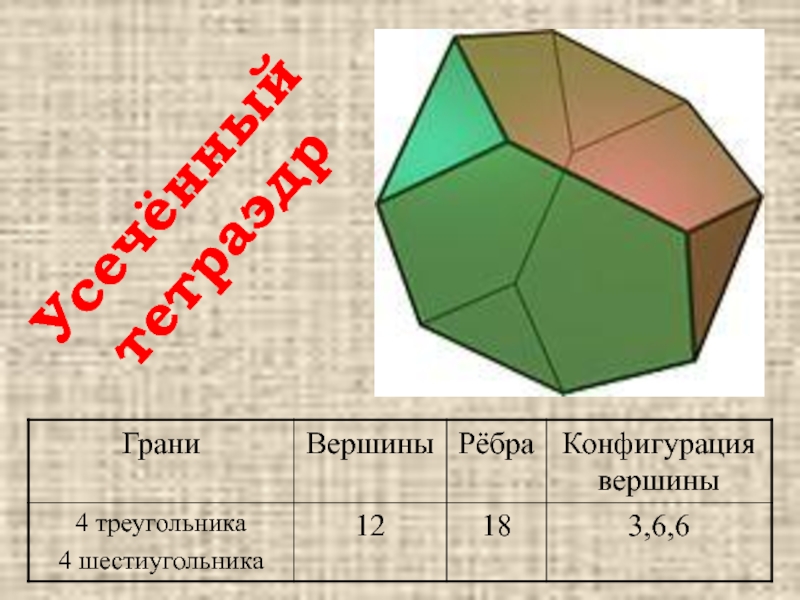
- 23. Усечённый тетраэдр
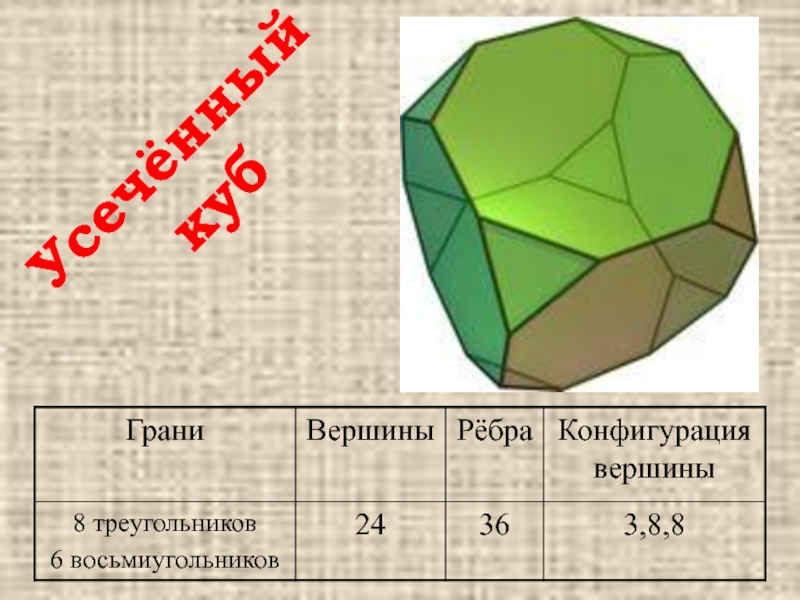
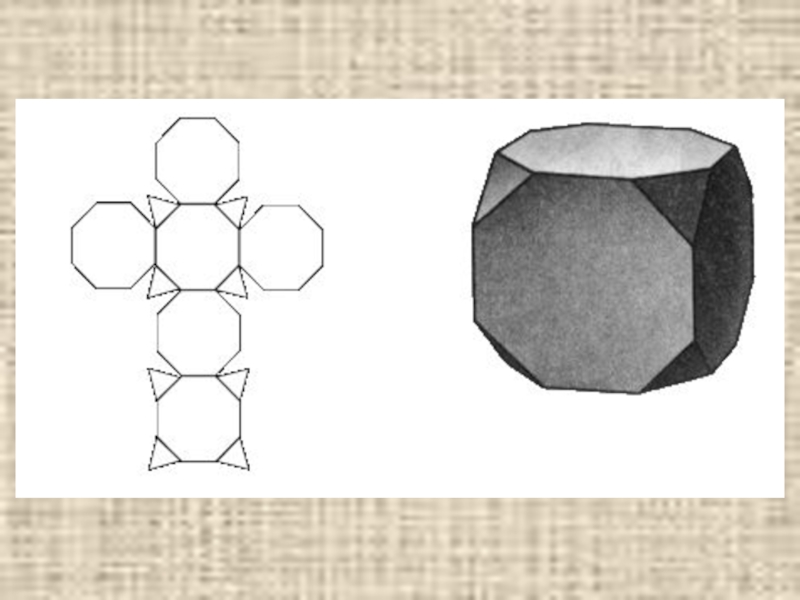
- 25. Усечённый куб
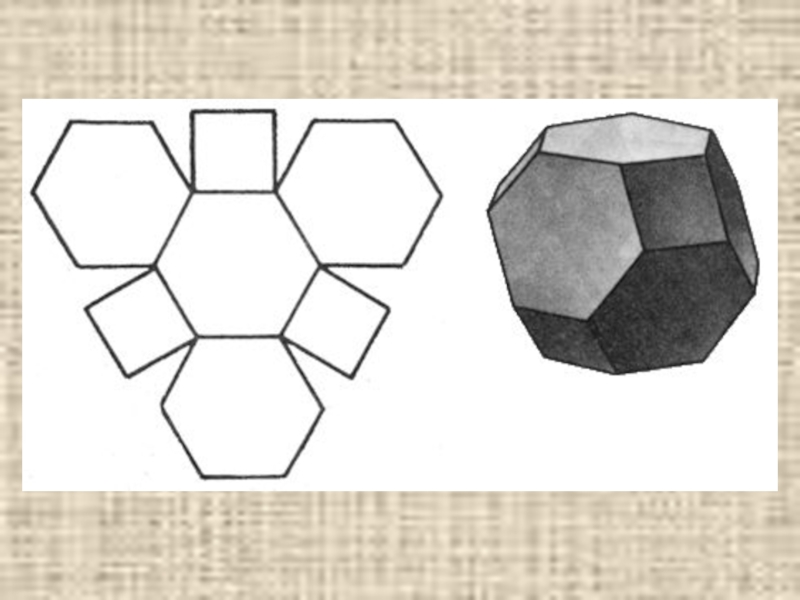
- 27. Усечённый октаэдр
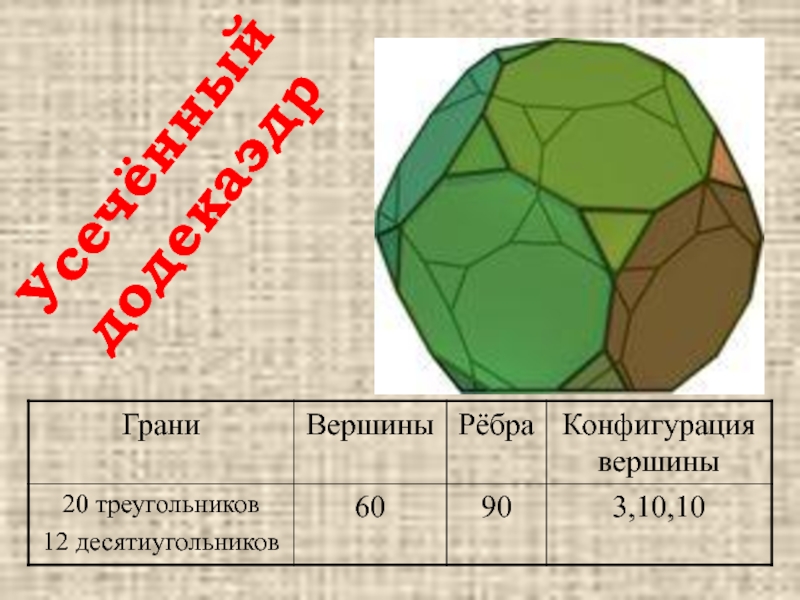
- 29. Усечённый додекаэдр
- 30. Усечённый икосаэдр
- 31. Ромбокубоктаэдр
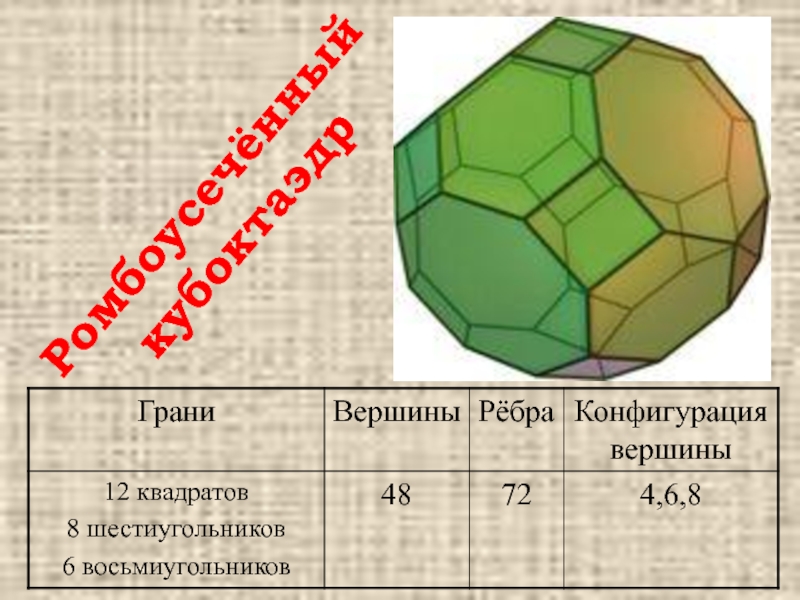
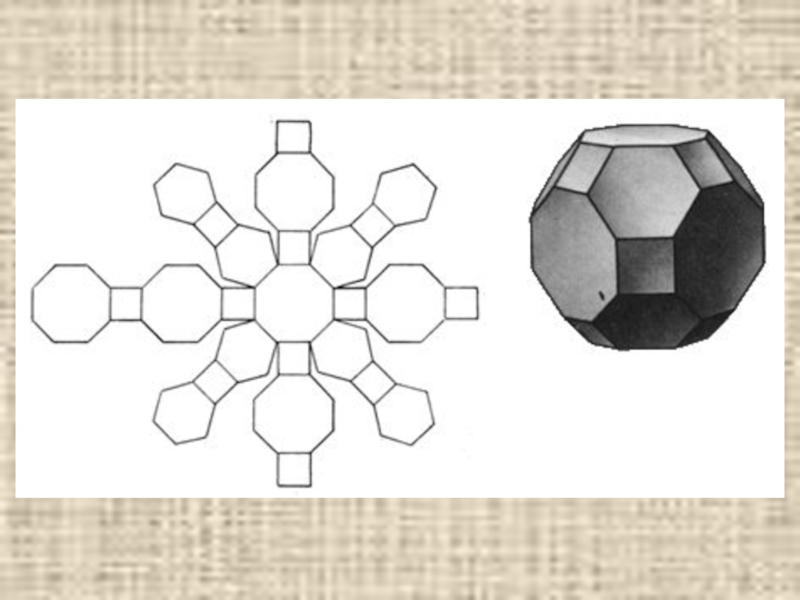
- 33. Ромбоусечённый кубоктаэдр
- 35. Ромбоикосододекаэдр
- 36. Ромбоусечённый икосододекаэдр
- 37. Курносый куб
- 38. Курносый додекаэдр
Слайд 2Многогранник называется правильным если все его грани – равные правильные многоугольники,
и в каждой вершине сходится одинаковое число рёбер.
Слайд 15
Многогранник называется равноугольно полуправильным или архимедовым, если все его многогранные углы
равны между собой, а все его грани — правильные, но разноимённые многоугольники.
Эти многогранники были впервые рассмотрены Архимедом в 111 в. до н. э., поэтому их называют телами Архимеда.
Затем все они были вновь открыты и описаны в эпоху Ренессанса. Известный немецкий астроном и математик Иоганн Кеплер (1571 — 1630) в книге «Гармония мира» в 1619 г. полностью восстановил потерянную информацию о них.
Эти многогранники были впервые рассмотрены Архимедом в 111 в. до н. э., поэтому их называют телами Архимеда.
Затем все они были вновь открыты и описаны в эпоху Ренессанса. Известный немецкий астроном и математик Иоганн Кеплер (1571 — 1630) в книге «Гармония мира» в 1619 г. полностью восстановил потерянную информацию о них.
Слайд 16Усеченный тетраэдр
Усеченный куб
Усеченный октаэдр
Усеченный додекаэдр
13 основных полуправильных многогранников
Слайд 17Усеченный икосаэдр
Кубоктаэдр
Икосододекаэдр
Ромбокубоктаэдр
13 основных полуправильных многогранников
Слайд 18Ромбоикосододекаэдр
Ромбоусечённый кубоктаэдр
Ромбоусечённый икосододекаэдр
Курносый куб
13 основных полуправильных многогранников
Слайд 19Курносый додекаэдр
13 основных полуправильных многогранников
Ещё один полуправильный многогранник
Псевдоромбокубоктаэдр
