- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Комплексные числа и координатная плоскость презентация
Содержание
- 1. Комплексные числа и координатная плоскость
- 2. Геометрическая модель множества R действительных чисел –
- 3. Добавив к числовой прямой, соответствующей множеству всех
- 4. Геометрический смысл операции сопряжения ! Операция сопряжения
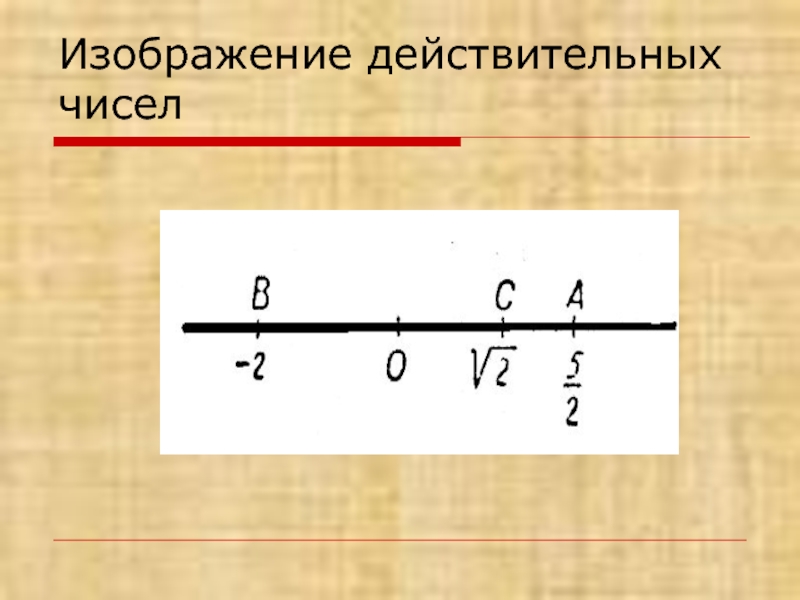
- 5. Изображение действительных чисел
- 6. Изображение комплексных чисел Алгебраический
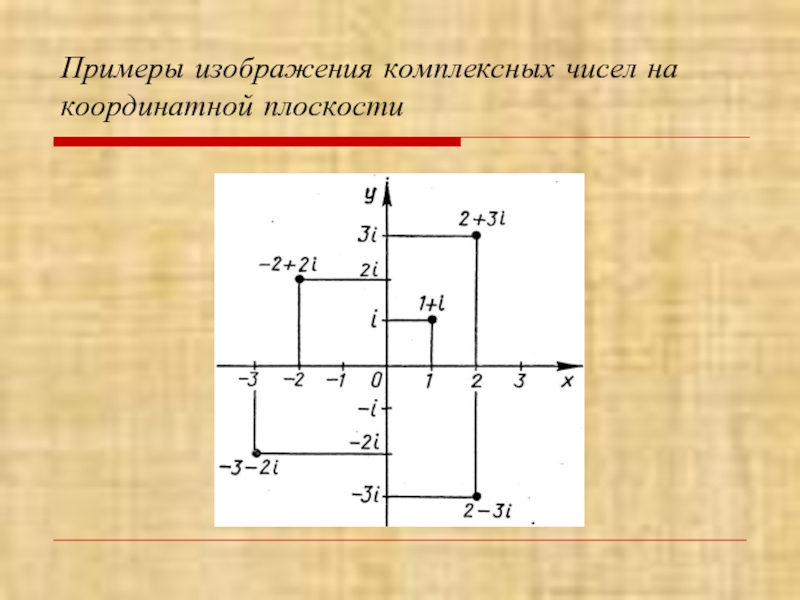
- 7. Примеры изображения комплексных чисел на координатной плоскости
- 8. Изобразите на координатной плоскости множество всех комплексных
- 9. Изобразите на координатной плоскости множество всех комплексных
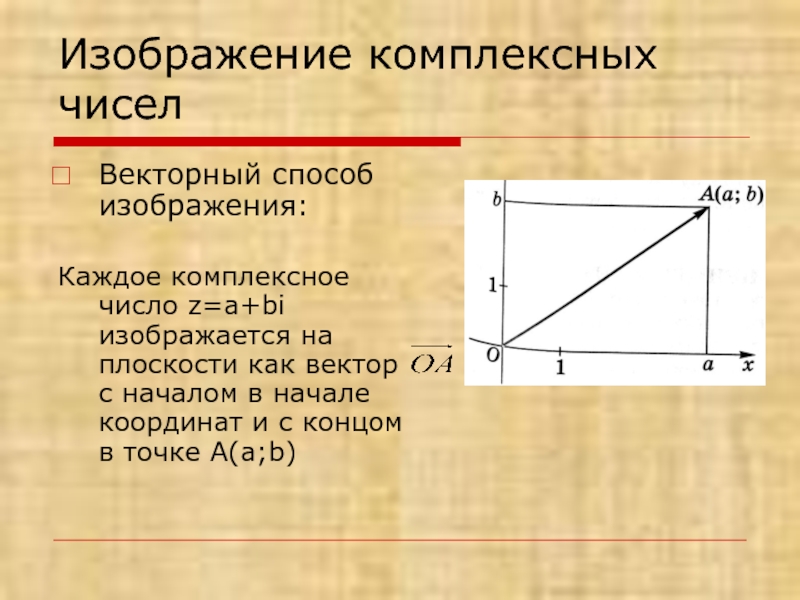
- 10. Изображение комплексных чисел Векторный способ изображения:
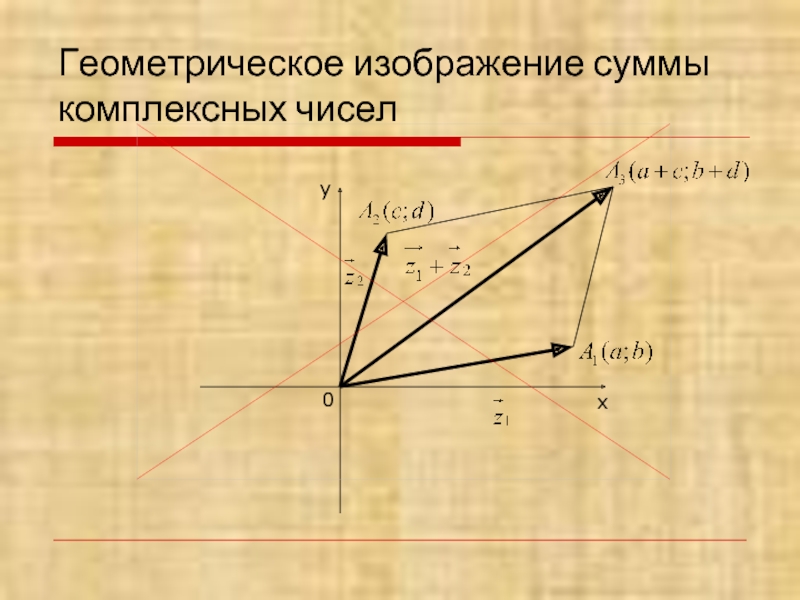
- 11. Геометрическое изображение суммы комплексных чисел х
- 12. Изображение противоположных комплексных чисел
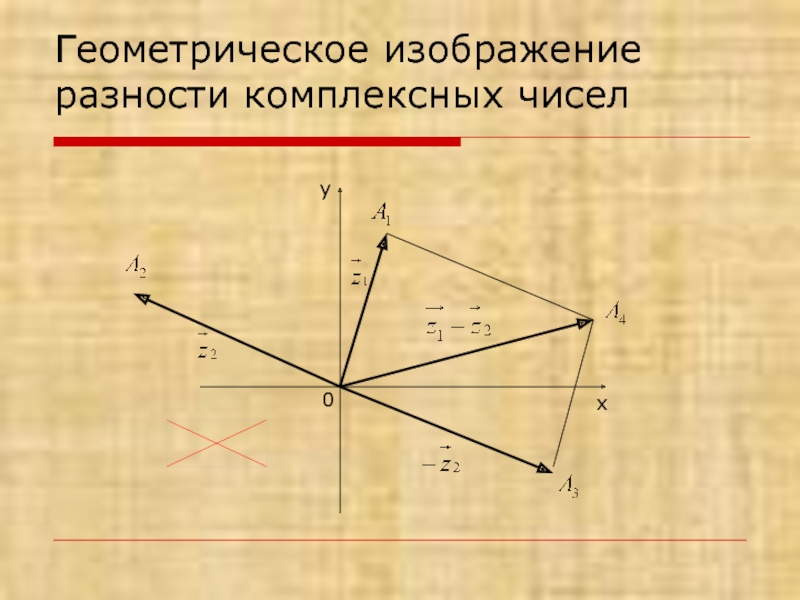
- 13. Геометрическое изображение разности комплексных чисел х
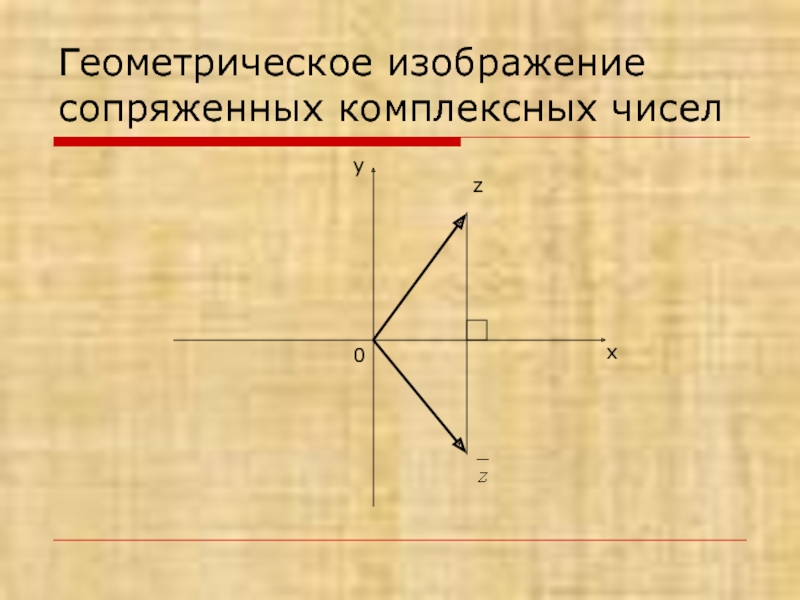
- 14. Геометрическое изображение сопряженных комплексных чисел х у 0 z
- 15. Спасибо за внимание
Слайд 2Геометрическая модель множества R действительных чисел – числовая прямая. Любому действительному числу
соответствует единственная точка на числовой прямой и, любой точке прямой соответствует только одно действительное число!
Слайд 3Добавив к числовой прямой, соответствующей множеству всех действительных чисел ещё одно
измерение – прямую, содержащую множество чисто мнимых чисел – получим координатную плоскость, в которой каждому комплексному числу a+bi можно поставить в соответствие точку (a; b) координатной плоскости.
i=0+1i соответствует точка (0;1)
2+3i соответствует точка (2;3)
-i-4 соответствует точка (-4;-1)
5=5+1i соответствует тоска (5;0)
Слайд 4Геометрический смысл операции сопряжения
! Операция сопряжения есть осевая симметрия относительно оси
абсцисс.
!! Сопряжённые друг другу комплексные числа равноудалены от начала координат.
!!! Вектора, изображающие сопряженные числа, наклонены к оси абсцисс под одинаковым углом, но расположены по разные стороны от этой оси.
Слайд 6Изображение комплексных чисел
Алгебраический способ изображения:
Комплексное число a+bi изображается
точкой плоскости с координатами (a;b)
Слайд 8Изобразите на координатной плоскости множество всех комплексных чисел,
у которых:
Действительная часть
равна -4
(Нас интересуют комплексные числа z=x+yi , у которых х=-4. Это-уравнение прямой, параллельной оси ординат)
(Нас интересуют комплексные числа z=x+yi , у которых х=-4. Это-уравнение прямой, параллельной оси ординат)
х
0
у
Х= - 4
Слайд 9Изобразите на координатной плоскости множество всех комплексных чисел,
у которых:
Мнимая часть
является четным однозначным натуральным числом
(Нас интересуют комплексные числа z=x+yi, у которых у=2,4,6,8. Геометрический образ состоит из четырех прямых,параллельных оси абсцисс)
(Нас интересуют комплексные числа z=x+yi, у которых у=2,4,6,8. Геометрический образ состоит из четырех прямых,параллельных оси абсцисс)
х
у
0
2
4
6
8
Слайд 10Изображение комплексных чисел
Векторный способ изображения:
Каждое комплексное число z=a+bi изображается на плоскости
как вектор с началом в начале координат и с концом в точке А(a;b)