- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Геометрический смысл линейного неравенства презентация
Содержание
- 1. Геометрический смысл линейного неравенства
- 2. Линейное неравенство a1x1+a2x2≥b на
- 3. Построить полуплоскость
- 4. Построить полуплоскость 1. Построим в системе
- 5. Построить полуплоскость 2. Определим, какую полуплоскость
- 6. Построить полуплоскость 2. Определим, какую полуплоскость
- 7. Построить полуплоскость 2. Определим, какую полуплоскость
- 8. Замечание Для проверки проще всего использовать начало
- 9. Для построения множества точек, удовлетворяющих системе
- 10. Построить область решений системы линейных неравенств:
- 11. Построить область решений системы неравенств Построим
- 12. Построить область решений системы неравенств Построим
- 13. Построить область решений системы неравенств Построим
- 14. Построить область решений системы неравенств Построим
- 15. Построить область решений системы неравенств Построим
- 16. Построить область решений системы неравенств Построим
- 17. Построить область решений системы неравенств Условие
- 18. Литература Данко П.Е., Попов А.Г., Кожевникова Т.Я.
Линейное неравенство a1x1+a2x2≥b на плоскости задает полуплоскость, границей которой является прямая a1x1+a2x2=b
Слайд 2
Линейное неравенство
a1x1+a2x2≥b
на плоскости задает полуплоскость, границей которой является прямая
a1x1+a2x2=b
Слайд 4
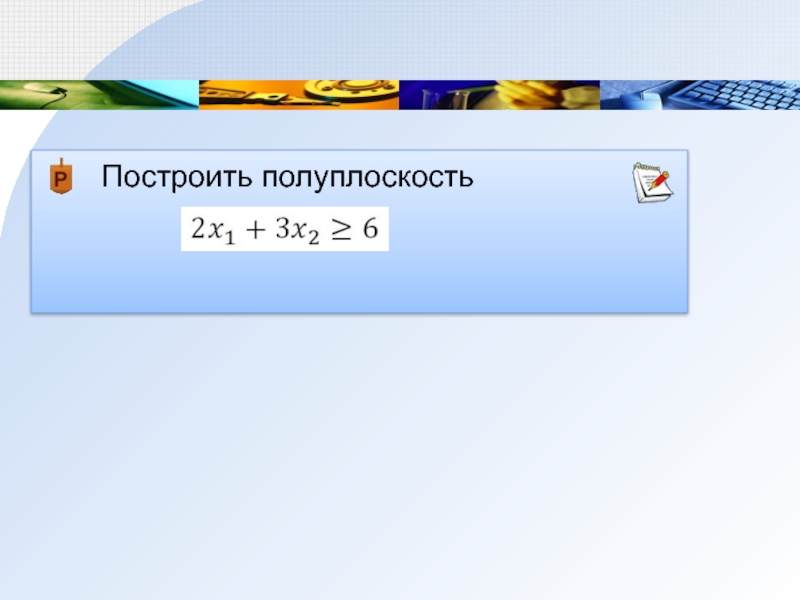
Построить полуплоскость
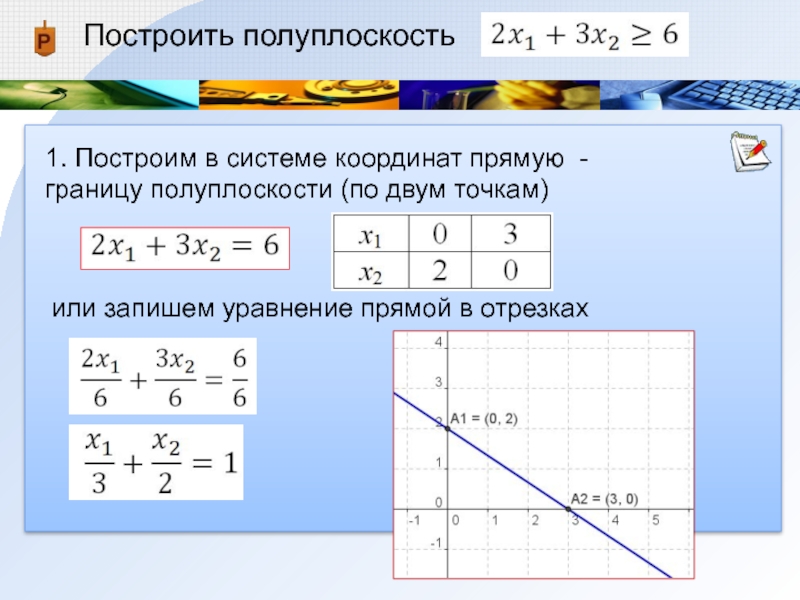
1. Построим в системе координат прямую - границу полуплоскости (по
двум точкам)
или запишем уравнение прямой в отрезках
Слайд 5
Построить полуплоскость
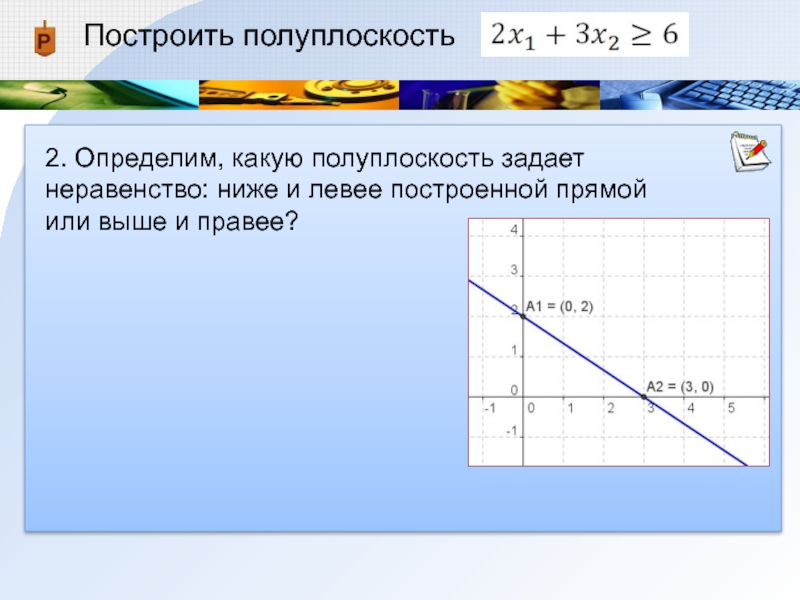
2. Определим, какую полуплоскость задает неравенство: ниже и левее построенной
прямой или выше и правее?
Слайд 6
Построить полуплоскость
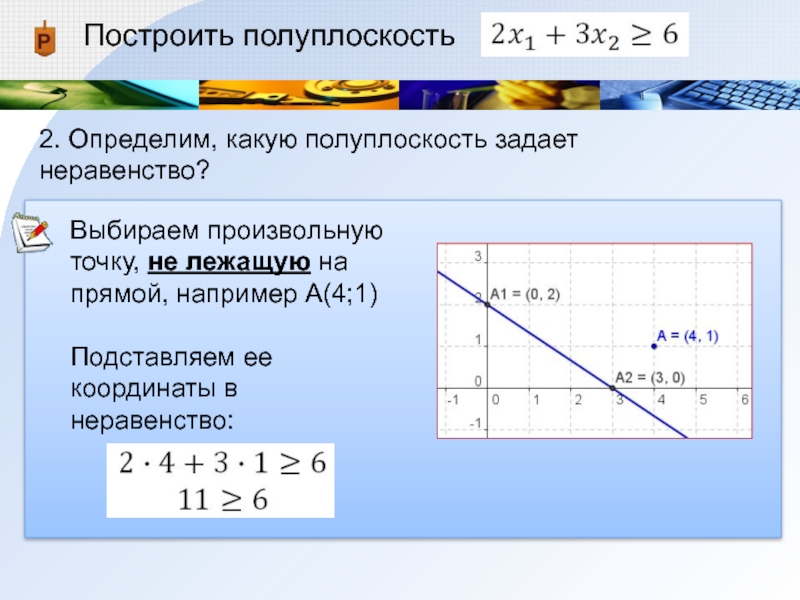
2. Определим, какую полуплоскость задает неравенство?
Выбираем произвольную точку, не лежащую
на прямой, например А(4;1)
Подставляем ее координаты в неравенство:
Подставляем ее координаты в неравенство:
Слайд 7
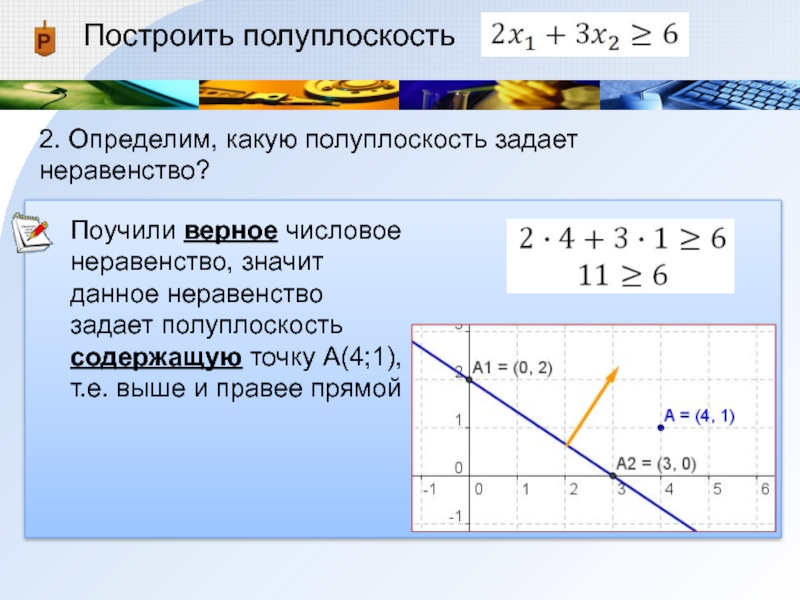
Построить полуплоскость
2. Определим, какую полуплоскость задает неравенство?
Поучили верное числовое неравенство, значит
данное неравенство задает полуплоскость содержащую точку А(4;1), т.е. выше и правее прямой
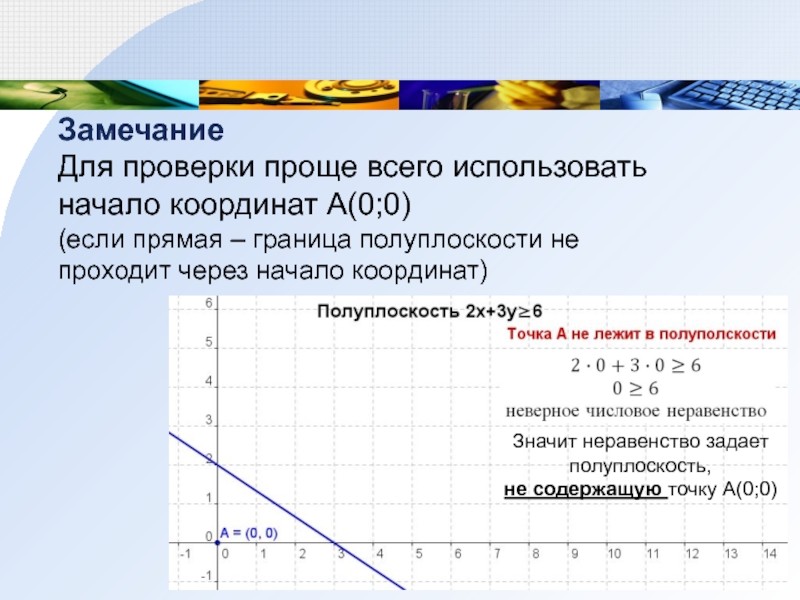
Слайд 8Замечание
Для проверки проще всего использовать начало координат А(0;0)
(если прямая –
граница полуплоскости не проходит через начало координат)
Значит неравенство задает полуплоскость,
не содержащую точку А(0;0)
Слайд 9
Для построения множества точек, удовлетворяющих системе линейных неравенств необходимо построить пересечение
полуплоскостей, заданных всеми неравенствами
Слайд 11Построить область решений системы неравенств
Построим полуплоскость, заданную первым неравенством x2-x1≤2
Граница полуплоскости:
x2-x1=2
Слайд 12Построить область решений системы неравенств
Построим полуплоскость, заданную первым неравенством x2-x1≤2
Определим полуплоскость
Подставим
координаты
точки А(0;0) в неравенство:
0 – 0 ≤ 2
0 ≤ 2 - верно
Значит полуплоскость
содержит начало координат
- точку А(0;0)
Слайд 13Построить область решений системы неравенств
Построим полуплоскость, заданную вторым неравенством 4x1+x2≥4
Граница полуплоскости:
4x1+x2=4
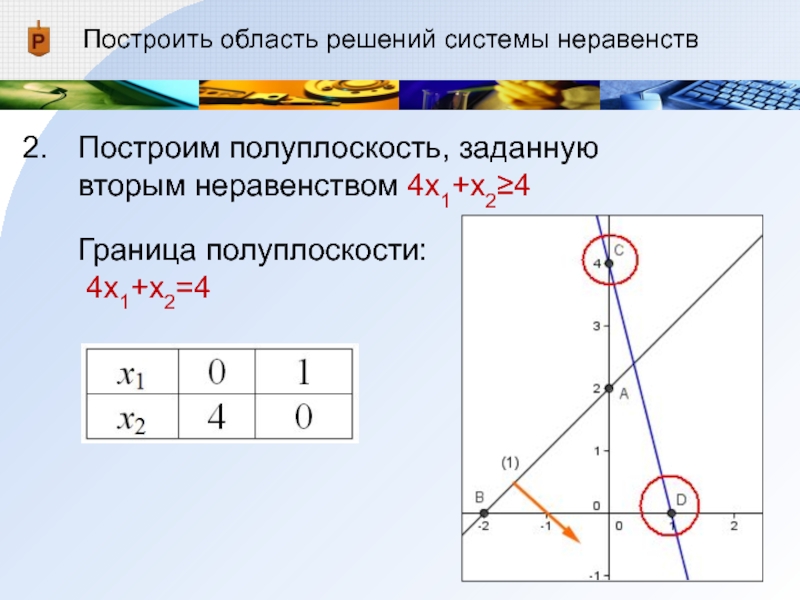
Слайд 14Построить область решений системы неравенств
Построим полуплоскость, заданную вторым неравенством 4x1+x2≥4
Определим полуплоскость
Подставим
координаты
точки А(0;0) в неравенство:
0 + 0 ≥ 4
0 ≥ 4 – не верно
Значит полуплоскость
не содержит начало
координат - точку А(0;0)
Слайд 15Построить область решений системы неравенств
Построим полуплоскость, заданную вторым неравенством x1+x2≤6
Граница полуплоскости:
x1+x2=6
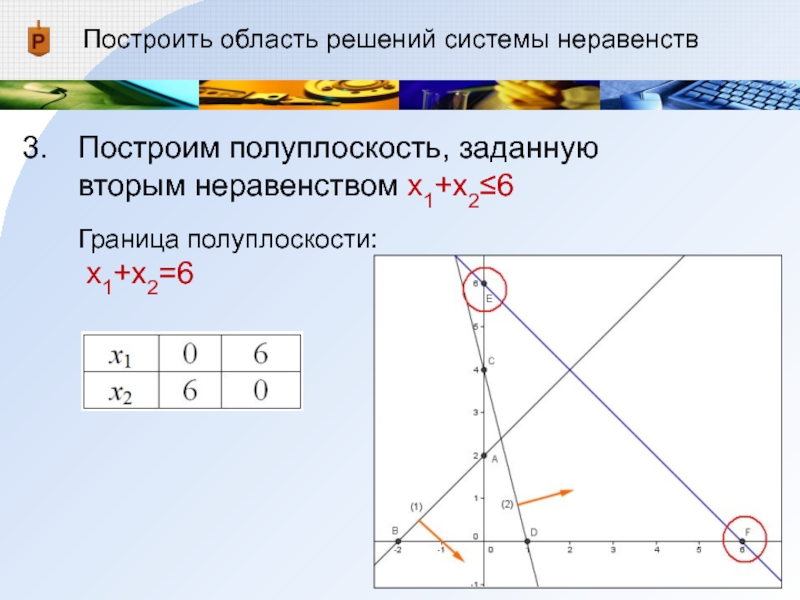
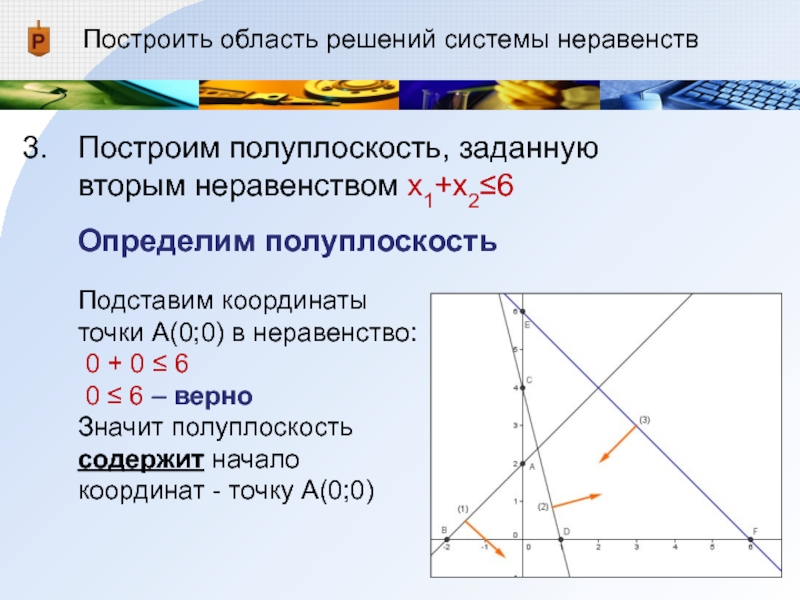
Слайд 16Построить область решений системы неравенств
Построим полуплоскость, заданную вторым неравенством x1+x2≤6
Определим полуплоскость
Подставим
координаты
точки А(0;0) в неравенство:
0 + 0 ≤ 6
0 ≤ 6 – верно
Значит полуплоскость
содержит начало
координат - точку А(0;0)
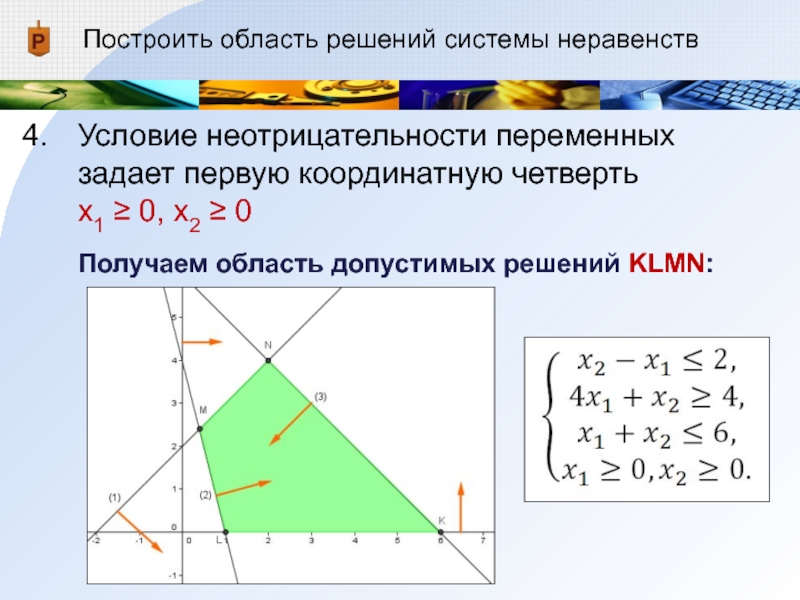
Слайд 17Построить область решений системы неравенств
Условие неотрицательности переменных задает первую координатную четверть
x1 ≥ 0, x2 ≥ 0
Получаем область допустимых решений KLMN:
Слайд 18Литература
Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и
задачах. Часть 1. - М.: Высшая школа, 1986. – C.271-274
