Выполнила:
Студента 1 Г курса
Дуленкова Анастасия
Проверила:
Преподаватель математики
Волчкова Наталья Николаевна
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Функции и их графики презентация
Содержание
- 1. Функции и их графики
- 2. ВВЕДЕНИЕ Возможно, мало, кто задумывается
- 3. В нашем проекте мы сделаем
- 4. ЦЕЛИ 1.расширение теоретических и практических знаний учащихся;
- 5. ЗАДАЧИ 1.обобщение знаний студентов по теме «Функции
- 6. ОБЪЕКТ ИССЛЕДОВАНИЯ процесс организации проектной деятельности по теме «Функции и их графики».
- 7. ПРЕДМЕТ ИССЛЕДОВАНИЯ Дидактические условия формирования познавательного интереса
- 8. ГИПОТЕЗА Если учитель в учебно-воспитательном процессе будет
- 10. И ВСЁ ЖЕ, ЧТО ТАКОЕ ФУНКЦИЯ И
- 11. ВИДЫ ФУНКЦИЙ: Линейная функция y = kx
- 12. ПРАКТИЧЕСКОЕ ПРИМЕНЕНИЕ ФУНКЦИЙ Функции применяются в точных,
- 13. Пример изображения исторических закономерностей. «График информационного бума» является графиком показательной функции.
- 14. Графики пословиц:
- 15. Дни солнцестояния Почему в марте долгота
- 16. График таяния льда С мороза в
- 17. Функциональные зависимости в химии:
- 18. Если бы все маковые зерна давали
- 19. ЗАКЛЮЧЕНИЕ Таким образом, исследование имеет
- 20. СПАСИБО ЗА ВНИМАНИЕ!
Слайд 1ПРЕЗЕНТАЦИЯ НА ТЕМУ: «ФУНКЦИИ И ИХ ГРАФИКИ»
Слайд 2ВВЕДЕНИЕ
Возможно, мало, кто задумывается о роли графиков функций, однако
Слайд 3 В нашем проекте мы сделаем попытку обсудить давно поставленный
Слайд 4ЦЕЛИ
1.расширение теоретических и практических знаний учащихся;
2.понимание и использование функциональных понятий
3.формирование умений строить графики элементарных функций;
4.понимание понятия функции как важнейшей математической модели для описания процессов и явлений окружающего мира.
5.проводить исследования, связанные с изучением свойств функций, на основе графиков изученных функций строить более сложные графики;
6.использовать функциональные представления и свойства функций для решения прикладных математических задач.
Слайд 5ЗАДАЧИ
1.обобщение знаний студентов по теме «Функции и их графики»;
2.обобщить, дополнить и
3.рассмотреть возможность применения вопросов, связанных с периодичностью функций, их монотонностью, нахождением промежутков убывания и возрастания, точек экстремума и экстремумов функций;
4.приобретение определенного опыта решения задач, связанных со знанием свойств функций.
5.вооружение учащихся специальными умениями, позволяющими им самостоятельно добывать знания по данной теме;
6.формирование устойчивого интереса к предмету, выявление и развитие математических способностей.
Слайд 6ОБЪЕКТ ИССЛЕДОВАНИЯ
процесс организации проектной деятельности по теме «Функции и их графики».
Слайд 7ПРЕДМЕТ ИССЛЕДОВАНИЯ
Дидактические условия формирования познавательного интереса к изучению и применению функций
Слайд 8ГИПОТЕЗА
Если учитель в учебно-воспитательном процессе будет использовать дополнительный материал, осуществлять проектную
- повысить математическую культуру учащихся при решении уравнений и неравенств с использованием свойств функций;
- облегчить процесс обучения методам решения более сложных задач, применяя характерные свойства функций;
- приобщить обучающихся к творческому поиску, учить формулировать и исследовать проблему.
Слайд 10И ВСЁ ЖЕ, ЧТО ТАКОЕ ФУНКЦИЯ И ЕЁ ГРАФИК?
Функция— закон зависимости
График функции — это геометрическое место точек плоскости, абсциссы (x) и ординаты (y) которых связаны указанной функцией:
точка располагается (или находится) на графике функции тогда и только тогда, когда .
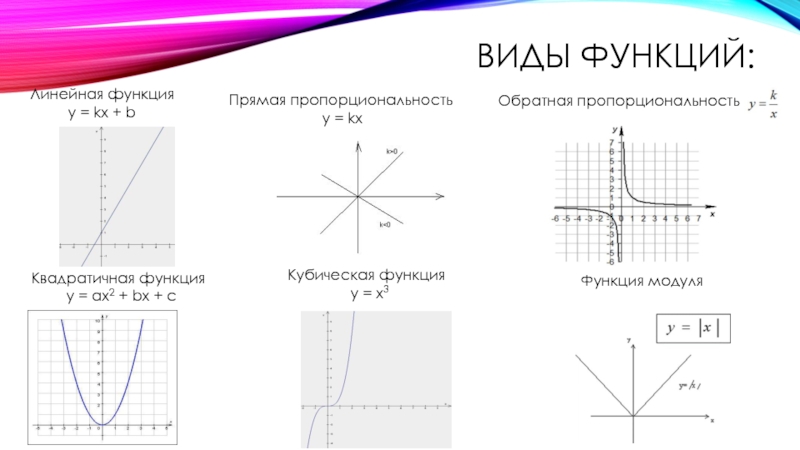
Слайд 11ВИДЫ ФУНКЦИЙ:
Линейная функция
y = kx + b
Прямая пропорциональность
y = kx
Обратная
Квадратичная функция
y = ax2 + bx + c
Кубическая функция
y = x3
Функция модуля
Слайд 12ПРАКТИЧЕСКОЕ ПРИМЕНЕНИЕ ФУНКЦИЙ
Функции применяются в точных, технических, общественных, естественных науках и
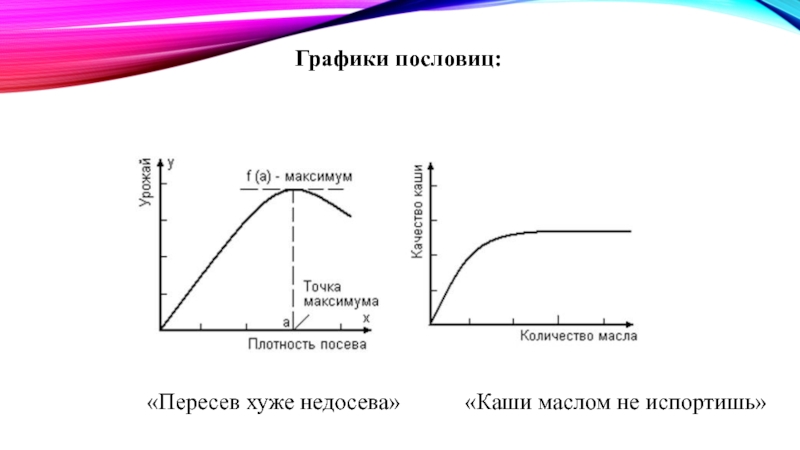
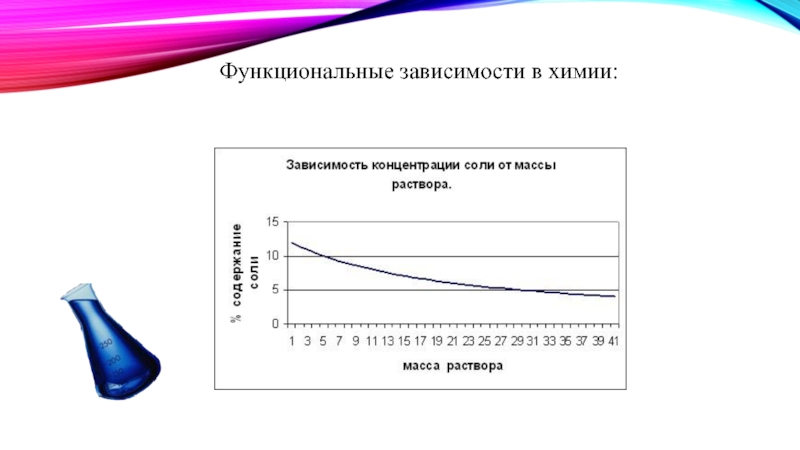
Они применяются в таких науках, как физика (например, изучение зависимости силы тока от напряжения),история, астрономия, социология (например, изменение роста численности населения), химия (например, зависимость концентрации соли от массы раствора), паремиология (например, графики пословиц), а также в жизни (например, график дней солнцестояния или график таяния льда)
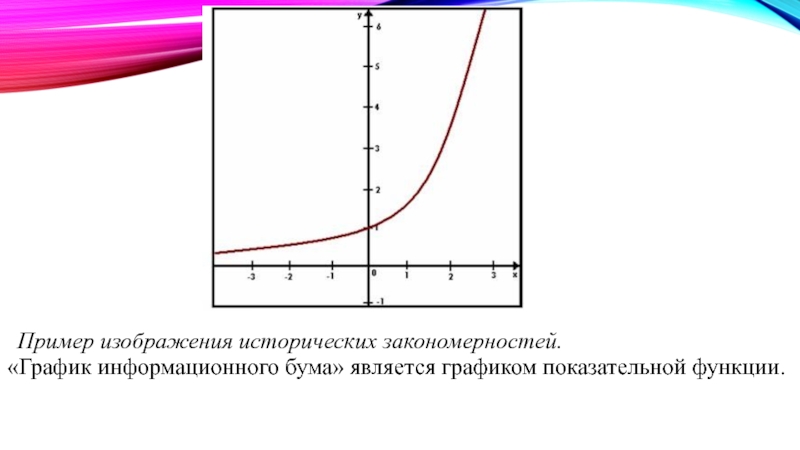
Слайд 13Пример изображения исторических закономерностей.
«График информационного бума» является графиком показательной функции.
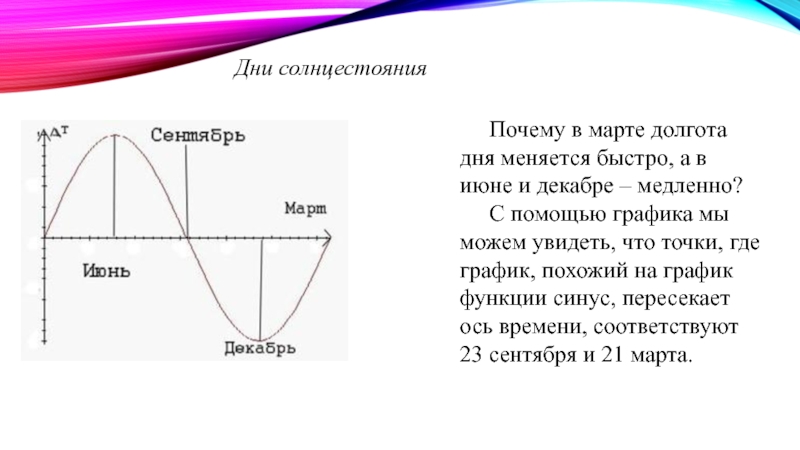
Слайд 15Дни солнцестояния
Почему в марте долгота дня меняется быстро, а в июне
С помощью графика мы можем увидеть, что точки, где график, похожий на график функции синус, пересекает ось времени, соответствуют 23 сентября и 21 марта.
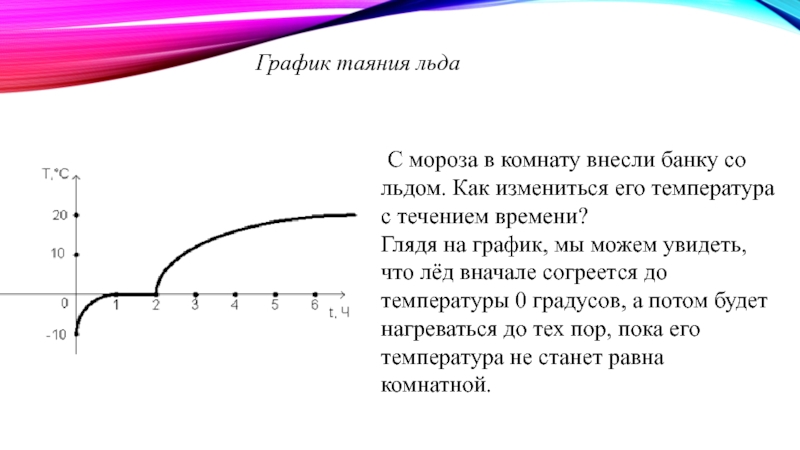
Слайд 16График таяния льда
С мороза в комнату внесли банку со льдом. Как
Глядя на график, мы можем увидеть, что лёд вначале согреется до температуры 0 градусов, а потом будет нагреваться до тех пор, пока его температура не станет равна комнатной.
Слайд 18
Если бы все маковые зерна давали всходы, то через 5 лет
Потомство комнатных мух за лето только от одной самки может составить 8 •1014
Применение понятия функции в естественных науках
Слайд 19ЗАКЛЮЧЕНИЕ
Таким образом, исследование имеет практические значении. В дальнейшем этот
Учащиеся должны уметь:
понимать и использовать функциональные понятия и язык;
строить графики элементарных функций; исследовать свойства числовых функций на основе изучения поведения их графиков;
понимать функцию как важнейшую математическую модель для описания процессов и явлений окружающего мира;
проводить исследования, связанные с изучением свойств функций; на основе графиков изученных функций строить более сложные графики;
использовать функциональные представления и свойства функций для решения математических задач из различных разделов курса.