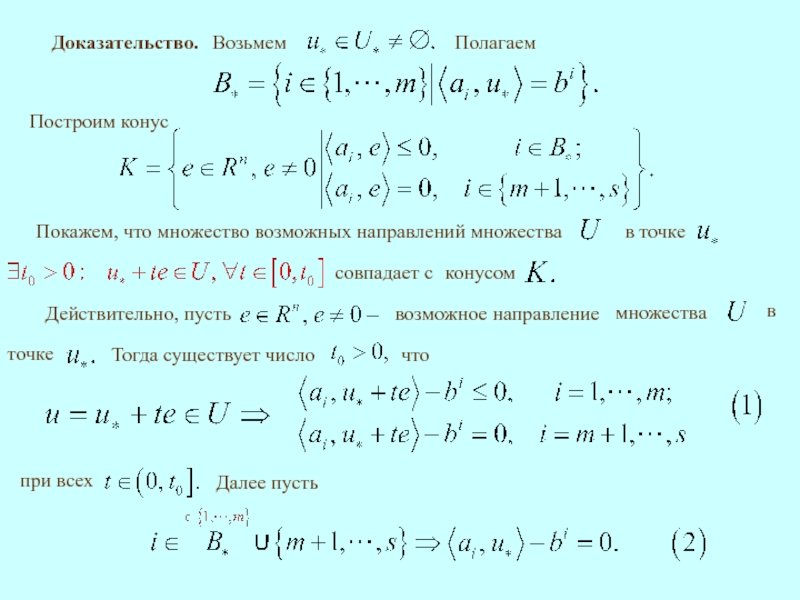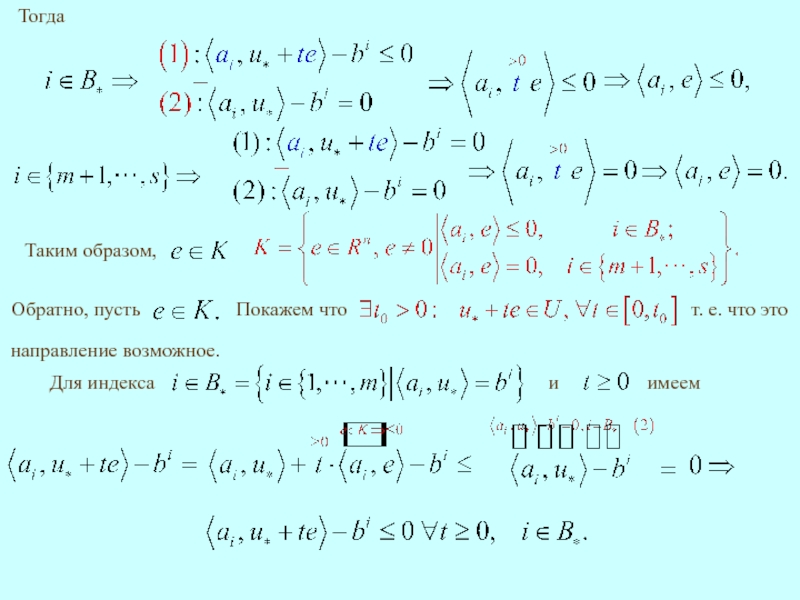- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Выпуклый анализ. Выпуклое программирование. Лекция 26 презентация
Содержание
Слайд 2
8. ВЫПУКЛОЕ ПРОГРАММИРОВАНИЕ
(ПРОДОЛЖЕНИЕ)
8.5. Теорема Куна - Таккера для многогранных множеств.
8.6. Теорема Куна – Таккера. Общий случай.
Слайд 6выполняется
Таким образом, соотношения (1)
установлены.
имеет место неравенство
Тогда из (3) выводим
Слайд 7В дальнейшем потребуется ссылка на теорему Фаркаша.
Теорема 6 (Фаркаша).
такие что
причем
Установим соответствие в обозначениях теоремы Фаркаша
и доказываемой теоремы
Слайд 8
Из теоремы Фаркаша следует
cсуществование векторов
таких, что
Доопределяем:
Тогда
Заметим, что
Слайд 10
Отсюда по теореме 1 заключаем,
Теорема доказана.
Из доказанной теоремы, в
имеющей конечное решение,
что точка
выполнено
8.6. Теорема Куна – Таккера. Общий случай.
Теорема 5.
Пусть в задаче выпуклого программирования
такая, что