исхода, которые условно назовем Успех и Неудача.
Например, студент сдает 4 экзамена, в каждом из которых возможно 2 исхода Успех: студент сдал экзамен и Неудача: не сдал.
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Схема Бернулли презентация
Содержание
- 1. Схема Бернулли
- 2. Вероятность Успеха в каждом испытании равна
- 3. В каждом случае Успех происходит m
- 4. Вероятность каждой такой комбинации по теореме
- 5. Формула Бернулли
- 6. ПРИМЕР. Известно, если монета упадет орлом,
- 7. Решение: По формуле Бернулли находим
- 8. Чтобы найти вероятность того, что при
- 9. Тогда вероятность искомого события составит
- 10. Наивероятнейшее число успехов в схеме Бернулли
- 11. Наивероятнейшее число успехов в схеме Бернулли Формула для наиболее вероятного числа успехов
- 12. Наивероятнейшее число успехов в схеме Бернулли
- 13. Наивероятнейшее число успехов в схеме Бернулли
- 14. Наивероятнейшее число успехов в схеме Бернулли
- 15. Наивероятнейшее число успехов в схеме Бернулли
- 16. Наивероятнейшее число успехов в схеме Бернулли
- 17. Наивероятнейшее число успехов в схеме Бернулли
- 18. Наивероятнейшее число успехов в схеме Бернулли
- 19. Наивероятнейшее число успехов в схеме Бернулли
- 20. Наивероятнейшее число успехов в схеме Бернулли
- 21. Наивероятнейшее число успехов в схеме Бернулли
- 22. Наивероятнейшее число успехов в схеме Бернулли
- 23. Наивероятнейшее число успехов в схеме Бернулли
- 24. Наивероятнейшее число успехов в схеме Бернулли
- 25. Наивероятнейшее число успехов в схеме Бернулли
- 26. Наивероятнейшее число успехов в схеме Бернулли
- 27. Схема Бернулли при больших n и
- 28. Теорема: Если вероятность p наступления события А
- 29. Обычно приближенную формулу Пуассона применяют, когда p
- 30. Пример Пусть известно, что при изготовлении некоторого
- 31. Пример Пусть известно, что при изготовлении некоторого
- 32. Пример Пусть известно, что при изготовлении некоторого
- 33. Пример В среднем по 1 % договоров страховая
- 34. Пример В среднем по 1 % договоров страховая
Вероятность Успеха в каждом испытании равна p. Вероятность Неудачи равна q=1-p. Требуется найти вероятность того, что в серии из n испытаний успех наступит m раз Pn(m)
Слайд 2
Вероятность Успеха в каждом испытании равна p. Вероятность Неудачи равна q=1-p.
Требуется найти вероятность того, что в серии из n испытаний успех наступит m раз
Pn(m)
Слайд 3
В каждом случае Успех происходит m раз, а Неудача (n-m) раз.
Число всех комбинаций равно числу способов из n испытаний выбрать те m, в которых был Успех, т.е.
Слайд 4
Вероятность каждой такой комбинации по теореме об умножении вероятностей составит Pmqn-m.
Так
как эти комбинации несовместны, то искомая вероятность события Bm будет
Слайд 6
ПРИМЕР.
Известно, если монета упадет орлом, студент
идет в кино, если монета
упадет решкой
– студент идет на лекцию. Монету бросило 5
студентов. Какова вероятность, что
трое из них окажутся на лекции
на лекции окажется не меньше 3 студентов
2) хотя бы один из студентов попадет на лекцию?
– студент идет на лекцию. Монету бросило 5
студентов. Какова вероятность, что
трое из них окажутся на лекции
на лекции окажется не меньше 3 студентов
2) хотя бы один из студентов попадет на лекцию?
Слайд 7
Решение:
По формуле Бернулли находим вероятность того, что при 5 бросаниях монеты
трижды случится успех:
В данной задаче проводится серия из n=5 независимых испытаний. Назовем Успехом поход на лекцию (выпадение решки) и Неудачей – поход в кино (выпадение герба).
p=q=1/2.
Слайд 8
Чтобы найти вероятность того, что при 5 бросаниях хотя бы один
раз монета выпадет решкой, перейдем к вероятности противоположного события - монета все 5 раз выпадет гербом:
Р5 (0).
Р5 (0).
Тогда искомая вероятность будет: Р=1- Р5(0).
По формуле Бернулли:
Слайд 10
Наивероятнейшее число успехов в схеме Бернулли
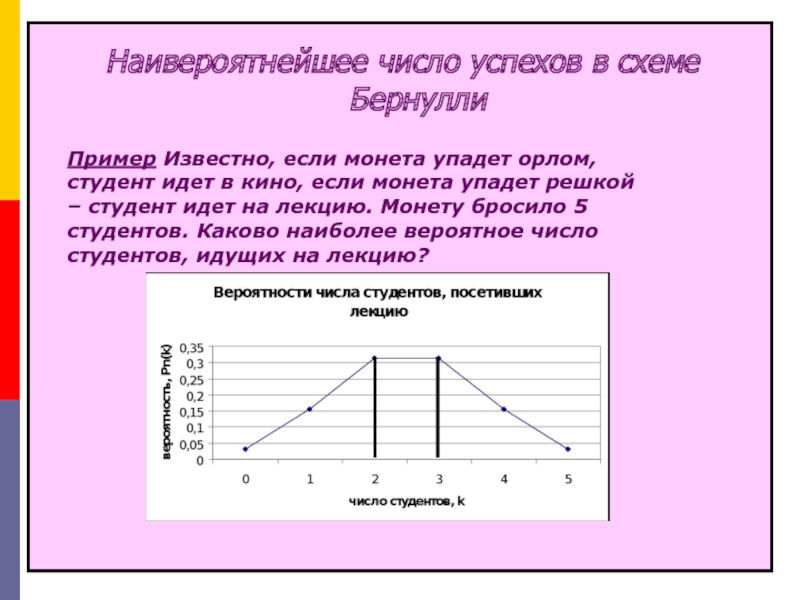
Пример Известно, если монета упадет орлом,
студент идет в кино, если монета упадет решкой – студент идет на лекцию. Монету бросило 5 студентов. Каково наиболее вероятное число студентов, идущих на лекцию?
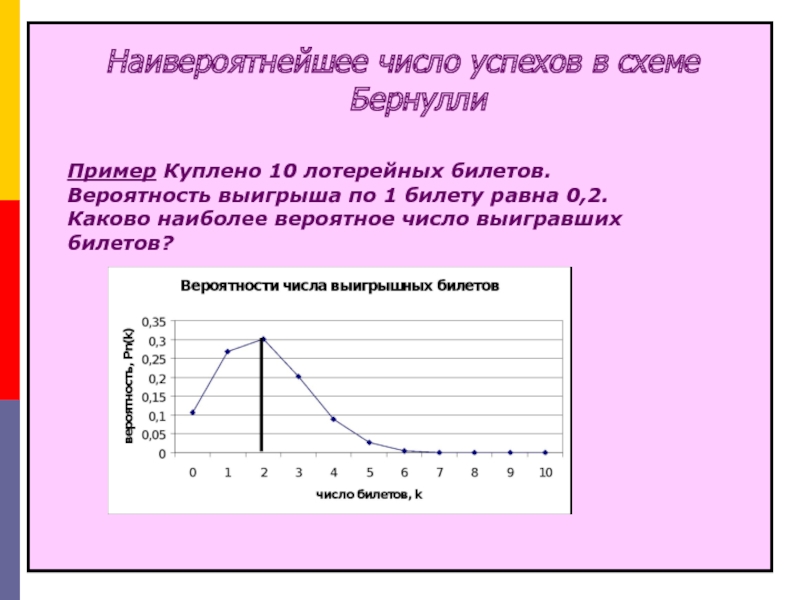
Пример Куплено 10 лотерейных билетов. Вероятность выигрыша по 1 билету равна 0,2. Каково наиболее вероятное число выигравших билетов?
Слайд 12
Наивероятнейшее число успехов в схеме Бернулли
Формула для наиболее вероятного числа успехов
Если np-q– целое число, то в этом интервале лежит 2 целых числа. Оба равновероятны.
Если np-q – нецелое число, то в этом интервале лежит 1 целое число
Слайд 13
Наивероятнейшее число успехов в схеме Бернулли
Пример Известно, если монета упадет орлом,
студент идет в кино, если монета упадет решкой
– студент идет на лекцию. Монету бросило 5 студентов. Каково наиболее вероятное число студентов, идущих на лекцию?
– студент идет на лекцию. Монету бросило 5 студентов. Каково наиболее вероятное число студентов, идущих на лекцию?
Слайд 14
Наивероятнейшее число успехов в схеме Бернулли
Пример Известно, если монета упадет орлом,
студент идет в кино, если монета упадет решкой
– студент идет на лекцию. Монету бросило 5 студентов. Каково наиболее вероятное число студентов, идущих на лекцию?
– студент идет на лекцию. Монету бросило 5 студентов. Каково наиболее вероятное число студентов, идущих на лекцию?
Слайд 15
Наивероятнейшее число успехов в схеме Бернулли
Пример Известно, если монета упадет орлом,
студент идет в кино, если монета упадет решкой
– студент идет на лекцию. Монету бросило 5 студентов. Каково наиболее вероятное число студентов, идущих на лекцию?
– студент идет на лекцию. Монету бросило 5 студентов. Каково наиболее вероятное число студентов, идущих на лекцию?
Слайд 16
Наивероятнейшее число успехов в схеме Бернулли
Пример Известно, если монета упадет орлом,
студент идет в кино, если монета упадет решкой
– студент идет на лекцию. Монету бросило 5 студентов. Каково наиболее вероятное число студентов, идущих на лекцию?
– студент идет на лекцию. Монету бросило 5 студентов. Каково наиболее вероятное число студентов, идущих на лекцию?
Слайд 17
Наивероятнейшее число успехов в схеме Бернулли
Пример Известно, если монета упадет орлом,
студент идет в кино, если монета упадет решкой
– студент идет на лекцию. Монету бросило 5 студентов. Каково наиболее вероятное число студентов, идущих на лекцию?
– студент идет на лекцию. Монету бросило 5 студентов. Каково наиболее вероятное число студентов, идущих на лекцию?
Слайд 18
Наивероятнейшее число успехов в схеме Бернулли
Пример Куплено 10 лотерейных билетов. Вероятность
выигрыша по 1 билету равна 0,2.
Каково наиболее вероятное число выигравших билетов?
Каково наиболее вероятное число выигравших билетов?
Слайд 19
Наивероятнейшее число успехов в схеме Бернулли
Пример Куплено 10 лотерейных билетов. Вероятность
выигрыша по 1 билету равна 0,2.
Каково наиболее вероятное число выигравших билетов?
Каково наиболее вероятное число выигравших билетов?
Слайд 20
Наивероятнейшее число успехов в схеме Бернулли
Пример Куплено 10 лотерейных билетов. Вероятность
выигрыша по 1 билету равна 0,2.
Каково наиболее вероятное число выигравших билетов?
Каково наиболее вероятное число выигравших билетов?
Слайд 21
Наивероятнейшее число успехов в схеме Бернулли
Пример Куплено 10 лотерейных билетов. Вероятность
выигрыша по 1 билету равна 0,2.
Каково наиболее вероятное число выигравших билетов?
Каково наиболее вероятное число выигравших билетов?
Слайд 22
Наивероятнейшее число успехов в схеме Бернулли
Пример Куплено 10 лотерейных билетов. Вероятность
выигрыша по 1 билету равна 0,2.
Каково наиболее вероятное число выигравших билетов?
Каково наиболее вероятное число выигравших билетов?
Слайд 23
Наивероятнейшее число успехов в схеме Бернулли
Пример В среднем по 20% договоров
страховая компания выплачивает страховую сумму. Заключено 10 договоров
а) Найти вероятность того, что по трем придется выплатить страховую сумму
б) Страховую сумму не придется выплачивать ни по одному из договоров
в) страховую сумму придется выплатить не более, чем по трем договорам
г) найти наиболее вероятное число договоров, по которым придется выплатить страховую сумму
а) Найти вероятность того, что по трем придется выплатить страховую сумму
б) Страховую сумму не придется выплачивать ни по одному из договоров
в) страховую сумму придется выплатить не более, чем по трем договорам
г) найти наиболее вероятное число договоров, по которым придется выплатить страховую сумму
Слайд 24
Наивероятнейшее число успехов в схеме Бернулли
Пример В среднем по 20% договоров
страховая компания выплачивает страховую сумму. Заключено 10 договоров
а) Найти вероятность того, что по трем придется выплатить страховую сумму
а) Найти вероятность того, что по трем придется выплатить страховую сумму
Слайд 25
Наивероятнейшее число успехов в схеме Бернулли
Пример В среднем по 20% договоров
страховая компания выплачивает страховую сумму. Заключено 10 договоров
б) Страховую сумму не придется выплачивать ни по одному из договоров
б) Страховую сумму не придется выплачивать ни по одному из договоров
Слайд 26
Наивероятнейшее число успехов в схеме Бернулли
Пример В среднем по 20% договоров
страховая компания выплачивает страховую сумму. Заключено 10 договоров
в) страховую сумму придется выплатить не более, чем по трем договорам
в) страховую сумму придется выплатить не более, чем по трем договорам
Слайд 27
Схема Бернулли при больших n и малых p
Если n велико, то
использование формулы
затруднительно
Поэтому применяются приближенные формулы
затруднительно
Поэтому применяются приближенные формулы
Слайд 28Теорема: Если вероятность p наступления события А
в каждом испытании близка
к нулю,
а число независимых испытаний n достаточно велико,
то вероятность Pn(m) того, что в n независимых испытаниях
событие А наступит m раз, приближенно равна:
где λ=np
Эта формула называется формулой Пуассона (закон редких событий)
а число независимых испытаний n достаточно велико,
то вероятность Pn(m) того, что в n независимых испытаниях
событие А наступит m раз, приближенно равна:
где λ=np
Эта формула называется формулой Пуассона (закон редких событий)
Схема Бернулли при больших n и малых p
Слайд 30Пример Пусть известно, что при изготовлении некоторого препарата
брак (количество упаковок,
не соответствующих стандарту)
составляет 0,2%. Оценить приближенно вероятность того, что
серди 1000 наугад выбранных упаковок окажутся три упаковки,
не соответствующие стандарту.
составляет 0,2%. Оценить приближенно вероятность того, что
серди 1000 наугад выбранных упаковок окажутся три упаковки,
не соответствующие стандарту.
Схема Бернулли при больших n и малых p
Слайд 31Пример Пусть известно, что при изготовлении некоторого препарата
брак (количество упаковок,
не соответствующих стандарту)
составляет 0,2%. Оценить приближенно вероятность того, что
серди 1000 наугад выбранных упаковок окажутся три упаковки,
не соответствующие стандарту.
составляет 0,2%. Оценить приближенно вероятность того, что
серди 1000 наугад выбранных упаковок окажутся три упаковки,
не соответствующие стандарту.
Схема Бернулли при больших n и малых p
Слайд 32Пример Пусть известно, что при изготовлении некоторого препарата
брак (количество упаковок,
не соответствующих стандарту)
составляет 0,2%. Оценить приближенно вероятность того, что
серди 1000 наугад выбранных упаковок окажутся три упаковки,
не соответствующие стандарту.
составляет 0,2%. Оценить приближенно вероятность того, что
серди 1000 наугад выбранных упаковок окажутся три упаковки,
не соответствующие стандарту.
Схема Бернулли при больших n и малых p
Слайд 33Пример В среднем по 1 % договоров страховая компания
выплачивает страховую сумму.
Найти вероятность того, что из
100 договоров с наступлением страхового случая будет
связано не более 5 договоров.
100 договоров с наступлением страхового случая будет
связано не более 5 договоров.
Схема Бернулли при больших n и малых p
Слайд 34Пример В среднем по 1 % договоров страховая компания
выплачивает страховую сумму.
Найти вероятность того, что из
100 договоров с наступлением страхового случая будет
связано не более 5 договоров.
100 договоров с наступлением страхового случая будет
связано не более 5 договоров.
Схема Бернулли при больших n и малых p
