- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Заочная школа презентация
Содержание
- 1. Заочная школа
- 2. План занятия: Разминка а) Устный счет б)
- 3. Устный счет Сумму смежных углов разделите на количество сторон квадрата.
- 4. 2. Возведите в квадрат количество букв в названии математического предложения, которое принимается без доказательства.
- 5. 3. Количество углов, образованных при пересечении двух
- 6. 4. К сумме углов треугольника прибавьте квадрат числа 4.
- 7. 5. От градусной меры прямого угла вычтите четвертую часть развернутого угла
- 8. 6. Количество признаков равенства треугольников умножьте на 20% от 150
- 9. 7. Показатель степени, в которую надо возвести
- 10. 8. Из Даты последнего дня февраля в високосном году вычтите квадрат числа 5.
- 11. 9. Число букв в названии самого большего колокола умножьте на число международного женского дня
- 12. 10. От количества букв в названии географического объекта «Урал» отнимите целую часть числа
- 13. 11. Количество признаков равенства треугольников умножьте на порядковый номер ноты «ля»
- 14. 12. Количество материков умножьте на количество океанов.
- 15. Признак делимости на «2» Знать обязательно каждому
- 16. Признак делимости на «3» Натуральные без всякого
- 17. Признак делимости на «5» О том, что
- 18. Задача №1. Возьмем самое маленькое число, которое
- 19. Задача №2. Из набора цифр 1, 2,…,
- 20. 1, 2, 3, 4, 5, 6, 7,
- 21. Задача №3. Можно ли разменять 25р. при
- 22. Задача №4. Имеется кусок плана месторасположения двух
- 23. Задача 5. Прямоугольник состоит из квадратов. Найдите
- 24. Задача №6. В озере, где обитали лягушки,
- 25. Задача №7. Школьники двух шестых классов изготовили
- 26. Задача №8. По всем вагоном пассажирского поезда
- 27. Задача №9. Докажите, что МЫШКА + КАМЫШ
- 28. Задача №10.Найдите последнюю цифру числа 19981998+19991999 Решение:
- 29. По страницам контрольных работ
- 30. Контрольная работа № 2 21. а) Среди
- 31. Ответ:
- 32. Контрольная работа № 2 24. В одном
- 33. Ответ 24. кв в одном подъезде подъезда,
- 34. Контрольная работа № 2 25.Было 10 листов
- 35. Ответ
- 36. Контрольная работа №3 67. Какое наибольшее количество
- 37. Ответ:
- 38. Контрольная работа №4 77. От прямоугольника
- 39. Ответ:
- 40. Контрольная работа №4 84. На столе лежали
- 41. Ответ:
- 42. Олимпиада 1. Существует ли число вида
- 43. Диофантовы уравнения
- 44. Н
- 45. 80 кг 20 кг ? 57
- 46. ? 17 кг 83 кг:16= 34
- 47. Н
- 48. Он рассматривал уравнения, которые сегодня мы записали
- 49. Задача 2. (одна из задач Диофанта)
- 50. Задача 3. У мальчика было 50 р.,
- 51. Задача 3. У мальчика было 50 р.,
Слайд 2План занятия:
Разминка
а) Устный счет
б) Запомни
в) Задачи
По страницам контрольных работ
Олимпиада
Новая тема
Рефлексия
Слайд 42. Возведите в квадрат количество букв в названии математического предложения, которое
Слайд 53. Количество углов, образованных при пересечении двух прямых секущей, умножьте на
Слайд 97. Показатель степени, в которую надо возвести 5, чтобы получилось 625,
Слайд 119. Число букв в названии самого большего колокола умножьте на число
Слайд 15Признак делимости на «2»
Знать обязательно каждому надо,
Чтоб получить без ошибки ответ:
Из
Четные числа, нечетные - нет
Слайд 16Признак делимости на «3»
Натуральные без всякого труда
Те лишь числа на
У которых сумма цифр, посмотри:
Без остатка тоже делиться на «3»
Слайд 17Признак делимости на «5»
О том, что не вернуть минуты вспять,
Давно по
А числа натуральные на «5»,
И те лишь числа делятся на «5»,
В конце которых нуль или пятерка.
Слайд 18Задача
№1. Возьмем самое маленькое число, которое делится на 2 и на
А.9; Б.32.; Г.24; Д.18.
В. 20;
Слайд 19Задача
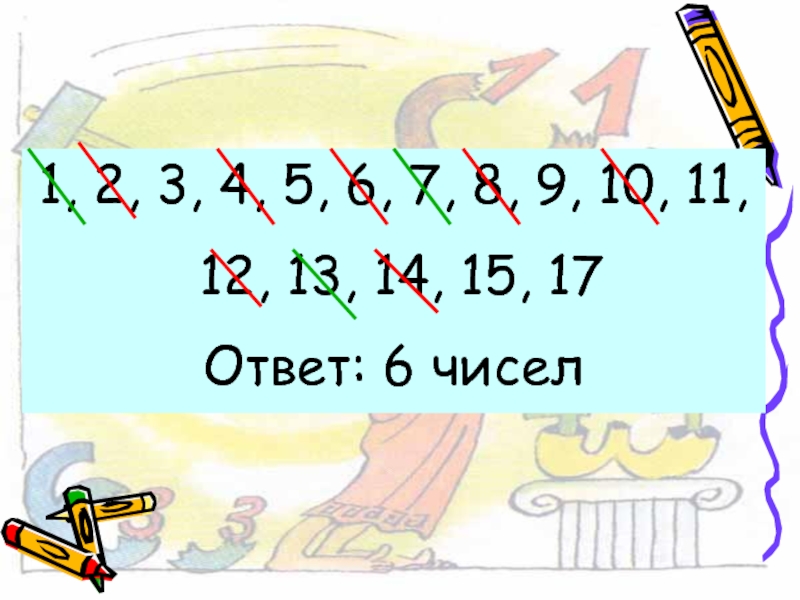
№2. Из набора цифр 1, 2,…, 17 вычеркнуты все четные числа,
Сколько чисел осталось?
; Б. 23; В. 24; Г. 25; Д. 8
А.6
Слайд 21Задача
№3. Можно ли разменять 25р. при помощи десяти купюр достоинством в
Решение: Десять купюр по 1, 3 и 5 р. Дают сумму из четного числа рублей, а 25 – число нечетное. Значит, 25 р. Нельзя разменять, как требуется в условии задачи.
Слайд 22Задача
№4. Имеется кусок плана месторасположения двух друзей. Можно ли определить, на
Слайд 23Задача
5. Прямоугольник состоит из квадратов. Найдите сторону самого большого квадрата, если
Ответ:
х+3=2х-1, х=4. Сторона большого квадрата х+3=4+3=7
Ответ: 7.
Слайд 24Задача
№6. В озере, где обитали лягушки, появилась лилия нового сорта. На
Слайд 25Задача
№7. Школьники двух шестых классов изготовили в школьных мастерских для детских
Ответ: 41.3=123
Слайд 26Задача
№8. По всем вагоном пассажирского поезда поровну разместили 737 туристов. Сколько
Решение: Число 737 надо представить в виде произведения двух множителей, где один будет означать количество вагонов поезда, а другой количество туристов в каждом вагоне:
737 = 11.67. Значит, в поезде 11 вагонов по 67 туристов в каждом вагоне
Слайд 27Задача
№9. Докажите, что МЫШКА + КАМЫШ не делится на 101.
Решение: МЫШКА+
а 7 . 11 . 13 . КА не делится на простое число 101, то и сумма 101 . МЫШ + 7 . 11 . 13 . КА не делится на 101, то есть МЫШКА + КАМЫШ не делится на 101, что и требовалось доказать.
Слайд 30Контрольная работа № 2
21. а) Среди всех чисел, больших 2000 и
найдите наименьшее;
б) Найдите наибольшее число, не превосходящее 10000 и дающее остаток 46 при делении на 94.
Слайд 32Контрольная работа № 2
24. В одном из подъездов восьмиэтажного дома на
Слайд 33Ответ
24. кв в одном подъезде
подъезда, тогда квартиры с 97 по 102
I подъезд с 1 по 48, II – с 49 по 96, III с 97 по 144, IV с 145 по 192. Значит 178 находиться в 4 подъезде на 6 этаже
Ответ: 4 подъезд, 6 этаж
Слайд 34Контрольная работа № 2
25.Было 10 листов бумаги. Некоторые из них разрезали
Слайд 36Контрольная работа №3
67. Какое наибольшее количество одинаковых букетов можно составить из
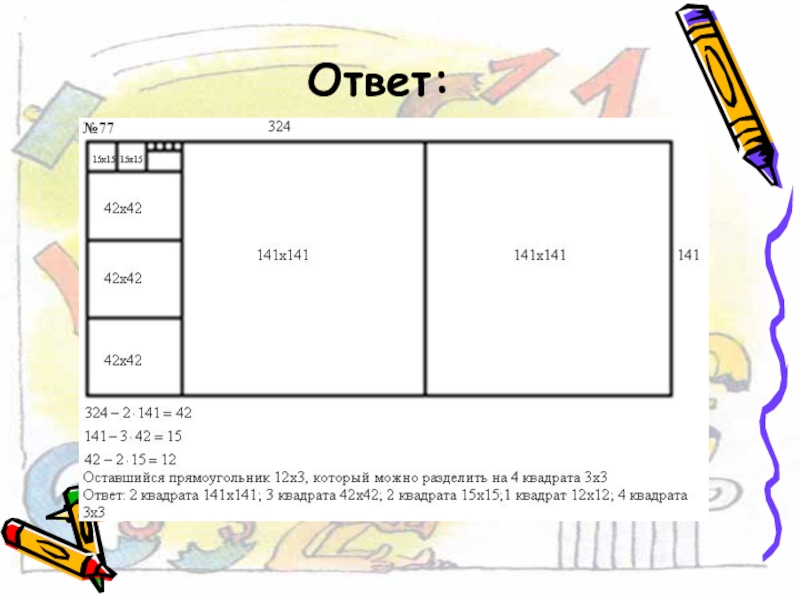
Слайд 38Контрольная работа №4
77. От прямоугольника 324х141 отрезают несколько квадратов со
Слайд 40Контрольная работа №4
84. На столе лежали книги. Их пытались связывать в
Слайд 42Олимпиада
1. Существует ли число вида 959595…95, которое делится на 1995
2. Когда солдаты строились в колонну по 4, по 5 или по 6 человек, то каждый раз один оставался лишним, а когда построились в колонну по 7, лишних не осталось. Каким могло быть наименьшее количество солдат?
3. Могут ли числа МЫШКА и КАМЫШ одновременно делится на 11?
4. Найдите последнюю цифру числа :
Слайд 44 Н а складе имеются гвозди
Задача 1.
Слайд 47 Н а складе имеются гвозди
Всего выдано 100 кг, отсюда уравнение:
16 х + 17 у + 40 z = 100
Решение.
Пусть ящиков по 16 кг х штук, по 17 кг – у штук, по 40 кг – z штук.
Ящиков по 40кг не может быть больше двух.
Два быть не может, т.к. 100 – 80 = 20, а 20 кг можно набрать, только вскрыв один ящик.
Пусть 1 ящик по 40 кг. Комбинируем другие ящики.
Пусть 1 ящик по 17 кг, тогда останется 43. Взять по 16 кг невозможно.
Пусть 2 ящика по 17 кг, тогда останется 26 кг. Целых ящиков по 16 кг не получится.
Пусть 3 ящика по 17 кг, тогда останется 9 кг, которые придется выдавать, вскрыв какой-нибудь ящик.
Значит, ящики по 40 кг нам не нужны.
Значит, получается уравнение:
16 х + 17 у = 100.
Перебирая варианты с 16 кг и 17 кг ящиками, получим единственное решение: 4 ящика по 17 кг и 2 ящика по 16 кг.
Задача 1.
Слайд 48Он рассматривал уравнения, которые сегодня мы записали бы, например, так:
ax +
где a, b и c целые числа, и ответ должен быть дан только в целых числах.
Такие уравнения называют «диофантовыми».
Диофант Александрийский
(II – III вв. до нашей эры).
Слайд 49Задача 2. (одна из задач Диофанта)
«Найти два числа, зная, что
Диофант рассуждает следующим образом:
Из условия задачи вытекает, что искомые числа не равны, так как произведение было бы не 96, а 100. Таким образом, одно из них будет больше половины их суммы, то есть 10 + х, другое же меньше, то есть 10 – х. Разность между ними 2х. Отсюда уравнение (10 + х)(10 - х) = 96 или Отсюда х = 2. Одно из искомых чисел равно 12, другое 8. Решение х = - 2 для Диофанта не существует, так как греческая математика знала только положительные числа.
Слайд 50Задача 3. У мальчика было 50 р., на которые он хотел
Всего имеется 50 р., отсюда
уравнение: 4 х + 3 у = 50
Решение.
Пусть марок по 4 р. х штук,
по 3 р. – у штук.
у = (50 - 4 х) : 3
у = (48 - 3 х) : 3 + (2 – х) : 3
у = 16 - х + (2 – х) : 3
a+c
b
?
a
b
c
b
+
=
Эта задача имеет не одно, а несколько решений.
Слайд 51Задача 3. У мальчика было 50 р., на которые он хотел
Решение. По 4 р. - х штук, по 3 р. – у штук.
Тогда 4 х + 3 у = 50; х0 = 2, у0 = 14 - решение
Итак, 4х + 3у =50;
4х0 + 3у0 = 50.
Если а= х – х0 и b=у – у0, то 4a + 3b = 0.
а делится на 3, а b на 4
Тогда а = 3k, b = -4k (k – любое целое число).
х – х0 = 3k х = 2 + 3k
у – у0 = -4k, т.е. у = 14 -4k.
Эта задача имеет не одно, а несколько решений.