Задачи:
изучить примеры действия с комплексными числами;
научиться решать уравнения с комплексными переменными;
изучить модуль и аргумент комплексного числа
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Задачи: изучить примеры действия с комплексными числами; научиться решать уравнения с комплексными переменными; изучить модуль и аргумент комплексного. презентация
Содержание
- 2. Цель работы - исследование истории
- 3. Тема: "Комплексные числа" Работу выполнила
- 4. «Мысль выражать все числа знаками настолько проста,
- 5. Слово «математика» возникло в Древней Греции
- 6. «МАТЕМА» Учение о числах (арифметика) Теория музыки
- 7. Число - одно из основных понятий математики, позволяющее выразить результаты счета или измерения "один" "много"
- 10. «урапун» - один «окоза» - два
- 11. Древнеегипетская нумерация 23 145
- 12. Древнеиндийская нумерация
- 13. Арабские цифры "Нуль" или "пусто" - "СИФРА"
- 15. Цифры русского народа
- 16. 3x2 + 6x + 5=0 a=3 b=6
- 17. КАРДАНО Джироламо 1501-1576 Жозеф Луи Лагранж
- 18. Мусхелишвили Николай Иванович Келдыш Мстислав
- 19. Комплексные числа
- 20. Соглашение о комплексных числах 3 + 0i = 3 -2 + 0i = -2
- 21. Сложение комплексных чисел (a + bi)+(a’ +
- 22. (-5 + 2i) – (3 – 5i)
- 23. Умножение комплексных чисел (a + bi) *
- 24. (7 – 4i) (3 – 2i) (3
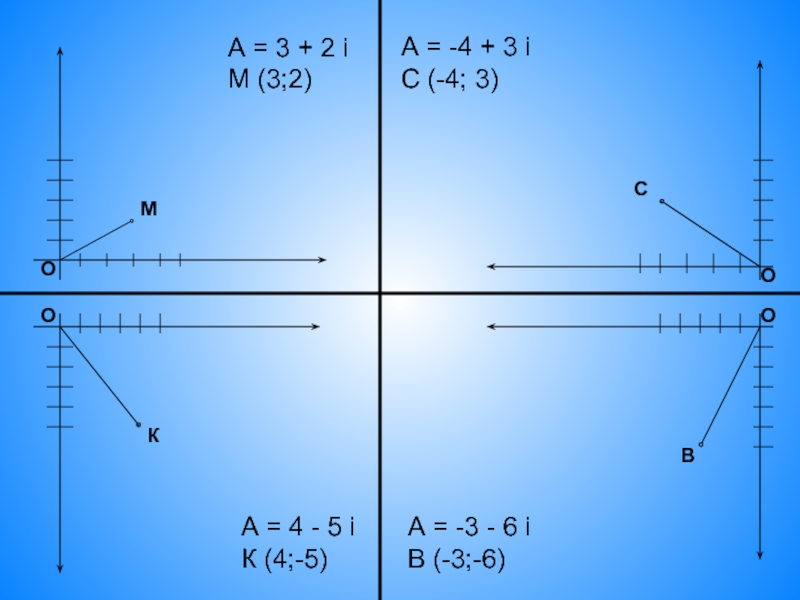
- 25. А = 3 + 2 i М
- 26. Решение уравнений с комплексными переменными
- 27. Модуль и аргумент комплексного числа r =
- 28. Теоретическая и практическая значимость реферата:
Цель работы - исследование истории
возникновения комплексных чисел,
связанной с необходимостью
выражения всех чисел знаками Задачи: изучить примеры действия с комплексными числами; научиться решать
Слайд 2Цель работы - исследование истории возникновения комплексных чисел, связанной с
необходимостью
выражения всех чисел знаками
Слайд 3Тема:
"Комплексные
числа"
Работу выполнила
Яковлева Алина,
ученица 8 "А" класса
Руководитель
Брылёва
К. И.
Слайд 4«Мысль выражать все числа знаками
настолько проста, что именно из-за
этой простоты
сложно осознать,
сколь она удивительна»
Пьер Симон Лаплас
сколь она удивительна»
Пьер Симон Лаплас
Слайд 5
Слово «математика» возникло в Древней Греции
примерно в V веке до
нашей эры
«Матема» - «учение»;
«знания, полученные через размышления»
«Матема» - «учение»;
«знания, полученные через размышления»
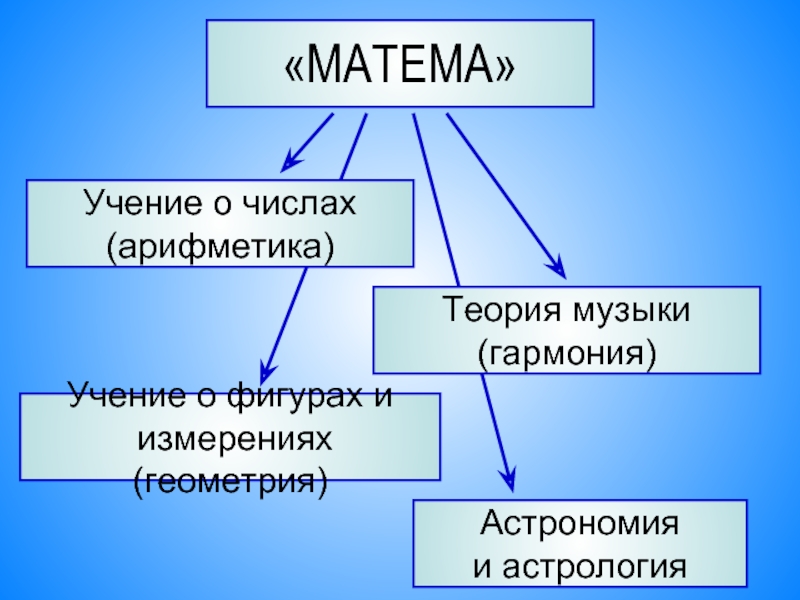
Слайд 6«МАТЕМА»
Учение о числах
(арифметика)
Теория музыки
(гармония)
Учение о фигурах и
измерениях (геометрия)
Астрономия
и астрология
Слайд 7Число - одно из основных понятий математики, позволяющее выразить результаты счета
или измерения
"один"
"много"
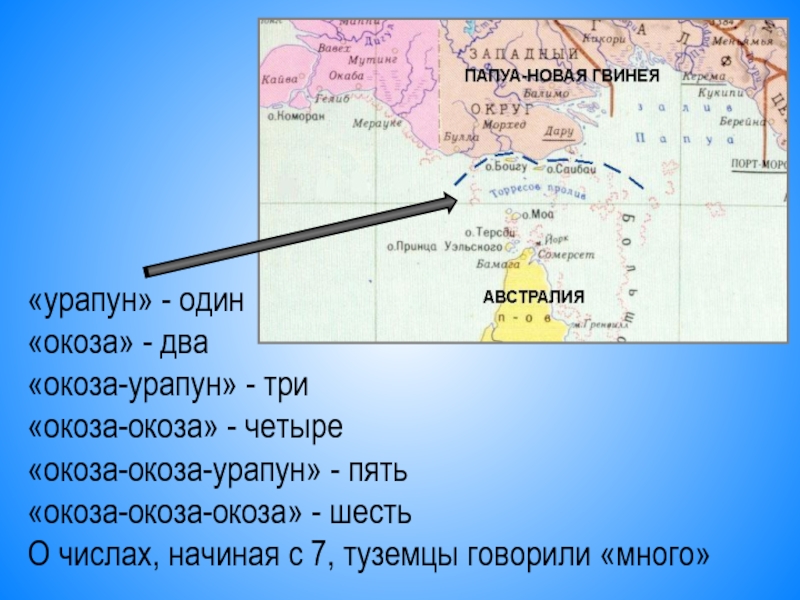
Слайд 10«урапун» - один
«окоза» - два
«окоза-урапун» - три
«окоза-окоза» - четыре
«окоза-окоза-урапун» - пять
«окоза-окоза-окоза» - шесть
О числах, начиная с 7, туземцы говорили «много»
Слайд 18Мусхелишвили Николай Иванович
Келдыш
Мстислав Всеволодович
Лаврентьев
Михаил Алексеевич
Боголюбов
Николай
Николаевич
Владимиров
Василий
Сергеевич
Сергеевич
Слайд 21Сложение комплексных чисел
(a + bi)+(a’ + b’i) = (a + a’)+(b
+ b’)i
(-3 + 5i) + (4 – 8i) = 1 - 3i
Слайд 22(-5 + 2i) – (3 – 5i) = -8 + 7i
Вычитание
комплексных чисел
(a + bi) – (a’ + b’i) = (a – a’) + (b – b’)i
Слайд 24(7 – 4i) (3 – 2i)
(3 - 2i) (3 + 2i)
Деление
комплексных чисел
(7 – 4i):(3 + 2i)
(13 – 26i)
13
= 1 – 2i
=
Слайд 28Теоретическая и практическая значимость реферата:
Данный материал можно использовать на
уроках математики для знакомства с комплексными числами в общеобразовательных классах;
Изучение данного материала формирует умение решать квадратные уравнения, когда дискриминант отрицательный;
В классах с углублённым изучением математики данный материал позволяет решать уравнения высших степеней
Изучение данного материала формирует умение решать квадратные уравнения, когда дискриминант отрицательный;
В классах с углублённым изучением математики данный материал позволяет решать уравнения высших степеней
