в Оглавление
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Презентация по геометрии на темы "Касательная к окружности" и "Вписанные, центральные углы." презентация
Содержание
- 1. Презентация по геометрии на темы "Касательная к окружности" и "Вписанные, центральные углы."
- 2. Если расстояние от центра окружности до прямой
- 3. Касательная к окружности Прямая, имеющая с окружностью
- 4. Касательная к окружности. Теорема: касательная окружности перпендикулярна
- 5. Отрезки касательных к окружности, проведенные из одной
- 6. Если прямая проходит через конец радиуса, лежащий
- 7. Угол с вершиной в центре окружности называется
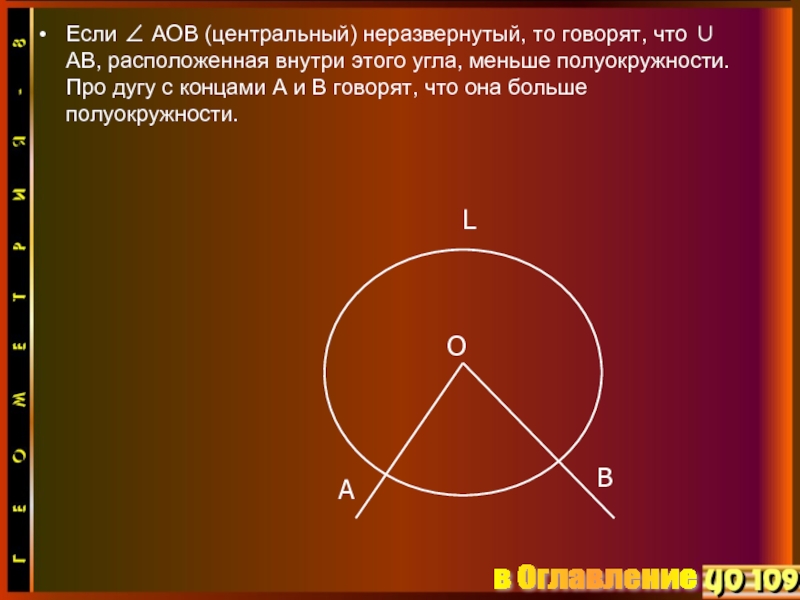
- 8. Если ∠ АОВ (центральный) неразвернутый, то говорят,
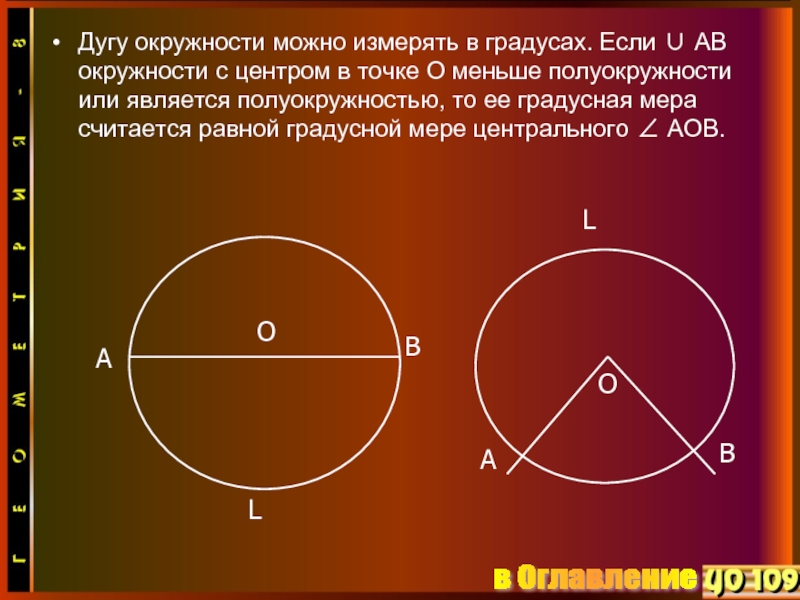
- 9. Дугу окружности можно измерять в градусах. Если
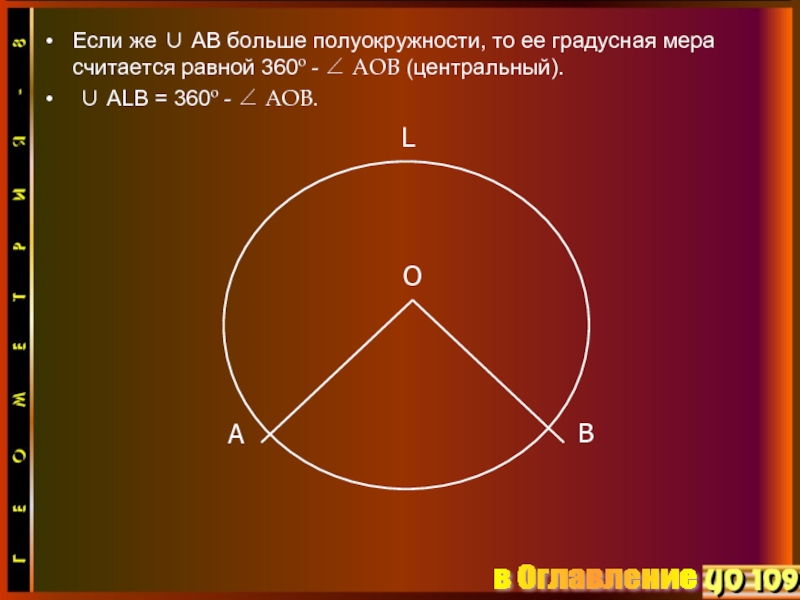
- 10. Если же ∪ АВ больше полуокружности, то
- 11. Угол вершина которого лежит на окружности, а
- 12. Вписанный угол измеряется половиной дуги на которую
- 13. Рассмотрим 1 случай расположения луча ВО относительно
- 14. Рассмотрим 2 случай, когда луч ВО делит
- 15. Рассмотрим 3 случай расположения луча ВО относительно
- 16. РАССМОТРИМ 1 СЛЕДСТВИЕ ИЗ ТЕОРЕМЫ Вписанные углы
- 17. Рассмотрим 2 следствие из теоремы Вписанный угол,
Слайд 1Презентация по геометрии на темы "Касательная к окружности" и "Вписанные, центральные
Слайд 2Если расстояние от центра окружности до прямой равно радиусу , то
касательная к окружности
r
H
M
O
в Оглавление
Слайд 3Касательная к окружности
Прямая, имеющая с окружностью только одну общую точку, называется
о
A
p
в Оглавление
Слайд 4Касательная к окружности.
Теорема: касательная окружности перпендикулярна к радиусу,проведенному в точку касания.
Доказательство:
Предположим,что это не так. Тогда радиус ОА является наклонной к прямой p.Так как перпендикуляр, проведенный из точки O к прямой p, меньше наклонной OA, то расстояние от центра О окружности до прямой p меньше радиуса. Следовательно, прямая p и окружность имеют две общие точки.Но это противоречит условию: прямая p-касательная.Таким образом,прямая p перпендикулярна к радиусу OA. Теорема доказана.
O
A
P
в Оглавление
Слайд 5Отрезки касательных к окружности, проведенные из одной точки, равны и составляют
По теореме о свойстве касательной ∠ 1 и ∠ 2 прямые, поэтому ΔАВО и ΔАСО прямоугольные. Они равны, так как имеют общую гипотенузу АО и равные катеты ОВ и ОС. Следовательно, АВ = АС и ∠ 3 = ∠ 4, что и требовалось доказать.
2
1
3
4
A
O
B
C
в Оглавление
Слайд 6Если прямая проходит через конец радиуса, лежащий на окружности, и перпендикулярна
Из условия теоремы следует, что радиус является перпендикуляром, проведенным из центра окружности к данной прямой. Поэтому расстояние от центра окружности до прямой равно радиусу, и следовательно, прямая и окружность имеет только одну общую точку. Но это и означает, что данная прямая является касательной к окружности.
Теорема доказана
в Оглавление
Слайд 7Угол с вершиной в центре окружности называется ее центральным углом .
Если ∠ АОВ развернутый, то ему соответствуют две полуокружности. ∪ ALB = 180º
Центральные углы
O
A
B
L
в Оглавление
Слайд 8Если ∠ АОВ (центральный) неразвернутый, то говорят, что ∪ АВ, расположенная
L
O
B
A
в Оглавление
Слайд 9Дугу окружности можно измерять в градусах. Если ∪ АВ окружности с
B
L
A
O
L
B
O
A
в Оглавление
Слайд 10Если же ∪ АВ больше полуокружности, то ее градусная мера считается
∪ ALB = 360º - ∠ АОВ.
L
B
O
A
в Оглавление
Слайд 11Угол вершина которого лежит на окружности, а стороны пересекают окружность, называется
Вписанный угол
B
O
C
M
A
в Оглавление
Слайд 12Вписанный угол измеряется половиной дуги на которую он опирается
Пусть ∠ АВС
в Оглавление
Слайд 13Рассмотрим 1 случай расположения луча ВО относительно ∠ АВС.
Например луч совпадает
O
B
2
1
C
A
в Оглавление
Слайд 14Рассмотрим 2 случай, когда луч ВО делит ∠ АВС на два
В этом случае луч ВО пересекает ∪ АС в некоторой точке D. Точка D разделяет ∪ АС на две дуги: АD и DC. По доказанному в п.1 ∠ АВD = 1/2 ∪AD и ∠ DBC= 1/2 ∪ DC. Складывая эти равенства попарно, получаем: ∠ ABD + ∠ DBC = 1/2 ∪ АD + 1/2 ∪ DC, или ∠ АВС= 1/2 ∪ АС.
A
B
C
D
в Оглавление
Слайд 15Рассмотрим 3 случай расположения луча ВО относительно ∠ АВС
АВD− равнобедренный,
Аналогично: ВСО равнобедр. ∠ COD - внешний, следовательно ∠ СВD= 1/2 ∪ CD.
Следовательно, ∠ АВС=1/2 ∪ АС
A
O
B
C
D
в Оглавление
Слайд 16РАССМОТРИМ 1 СЛЕДСТВИЕ ИЗ ТЕОРЕМЫ
Вписанные углы , опирающиеся на одну и
в Оглавление
Слайд 17Рассмотрим 2 следствие из теоремы
Вписанный угол, опирающийся на полуокружность − прямой.
в Оглавление