Содержание лекции:
Предмет и задачи курса
Понятие «имитационная математическая модель»
Основное предположение имитационного моделирования
Последовательность разработки имитационной модели
Требования к соотношениям имитационных моделей
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Лекция 1. Технология разработки имитационных моделей аграрных систем презентация
Содержание
- 1. Лекция 1. Технология разработки имитационных моделей аграрных систем
- 2. Технология разработки имитационных моделей аграрных систем^p(c) Н.М.
- 3. Технология разработки имитационных моделей аграрных систем^p(c) Н.М.
- 4. Технология разработки имитационных моделей аграрных систем^p(c) Н.М.
- 5. Технология разработки имитационных моделей аграрных систем^p(c) Н.М.
- 6. Технология разработки имитационных моделей аграрных систем^p(c) Н.М.
- 7. Технология разработки имитационных моделей аграрных систем^p(c) Н.М.
- 8. Технология разработки имитационных моделей аграрных систем^p(c) Н.М.
- 9. Технология разработки имитационных моделей аграрных систем^p(c) Н.М.
- 10. Технология разработки имитационных моделей аграрных систем^p(c) Н.М.
Слайд 1Технология разработки имитационных моделей аграрных систем^p(c) Н.М. Светлов, 2006.
Лекция 1. Технология
Слайд 2Технология разработки имитационных моделей аграрных систем^p(c) Н.М. Светлов, 2006.
Литература
1. Худякова Е.В., Липатов А.А.
2. Светлов Н.М. Альбом наглядных пособий к лекциям по курсу «Моделирование микро- и макроэкономических процессов» для студентов сельскохозяйственных вузов. М.: ЦОП РГАУ-МСХА имени К.А. Тимирязева, 2006.
3. Рабочая программа учебной дисциплины «Имитационное моделирование» / Сост. Н.М. Светлов. М.: РГАУ-МСХА имени К.А. Тимирязева, 2006. http://svetlov.timacad.ru/umk4/immod.doc
Слайд 3Технология разработки имитационных моделей аграрных систем^p(c) Н.М. Светлов, 2006.
1. Предмет и
Предмет курса — имитационные математические модели
Объект курса — аграрные системы
Задачи курса:
получить представление об имитационных моделях (ИМ), технологии их разработки, компьютерной реализации, подгонки и эксплуатации;
создать основу для самостоятельного накопления опыта разработки ИМ.
Слайд 4Технология разработки имитационных моделей аграрных систем^p(c) Н.М. Светлов, 2006.
2. Понятие «имитационная
Цели моделирования бывают следующими:
a) обеспечить достижение цели управления объектом моделирования;
b) изучить свойства объекта, закономерности, определяющие его поведение;
c) понять, что произойдёт, если воздействовать на объект тем или иным образом;
d) наконец, бывает так, что предстоящее использование модели неизвестно.
Слайд 5Технология разработки имитационных моделей аграрных систем^p(c) Н.М. Светлов, 2006.
2. Понятие «имитационная
Обычно считают, что имитационная модель, в отличие от других типов моделей, предназначена для постановки на ней многочисленных экспериментов со случайными значениями входных переменных и последующей статистической обработкой результатов.
В более широком смысле имитационная модель представляет собой описание структуры объекта, не содержащее информации о цели, которую мы желаем достичь, и о предполагаемых воздействиях на объект извне.
Имитационная модель разрабатывается таким образом, чтобы эту информацию можно было тем или иным способом сообщить модели в процессе её эксплуатации.
Слайд 6Технология разработки имитационных моделей аграрных систем^p(c) Н.М. Светлов, 2006.
2. Понятие «имитационная
Имитационная модель:
предназначена для имитации функционирования объекта моделирования;
не зависит от конкретной цели, для которой предпринимается имитация;
используется для постановки на ней компьютерных экспериментов (машинной имитации).
Слайд 7Технология разработки имитационных моделей аграрных систем^p(c) Н.М. Светлов, 2006.
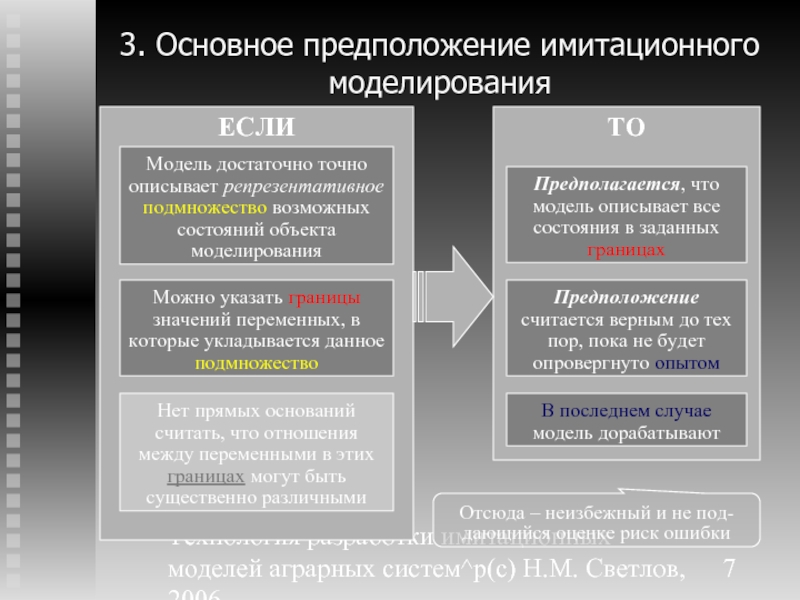
3. Основное предположение
ЕСЛИ
Модель достаточно точно описывает репрезентативное подмножество возможных состояний объекта моделирования
Можно указать границы значений переменных, в которые укладывается данное подмножество
Нет прямых оснований считать, что отношения между переменными в этих границах могут быть существенно различными
ТО
Предполагается, что модель описывает все состояния в заданных границах
Предположение считается верным до тех пор, пока не будет опровергнуто опытом
Отсюда – неизбежный и не под-дающийся оценке риск ошибки
В последнем случае модель дорабатывают
Слайд 8Технология разработки имитационных моделей аграрных систем^p(c) Н.М. Светлов, 2006.
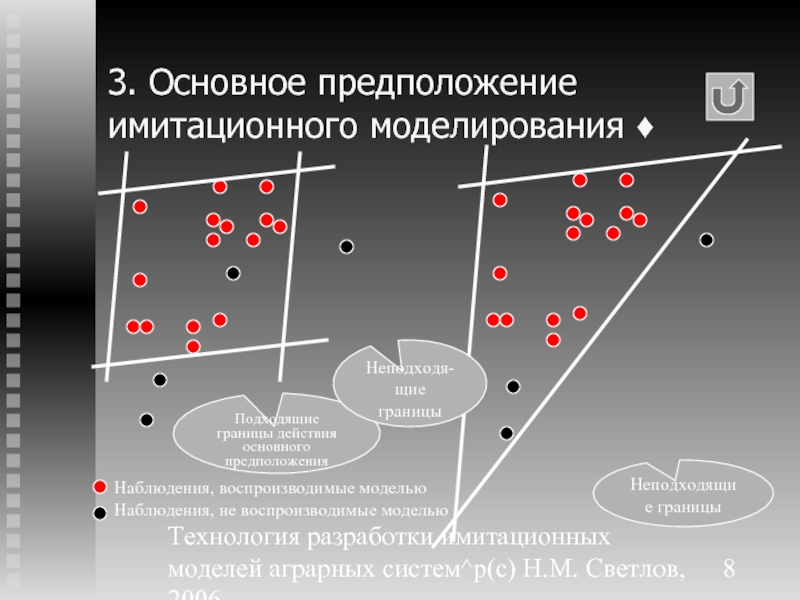
3. Основное предположение
Наблюдения, воспроизводимые моделью
Наблюдения, не воспроизводимые моделью
Подходящие границы действия основного предположения
Неподходящие границы
Слайд 9Технология разработки имитационных моделей аграрных систем^p(c) Н.М. Светлов, 2006.
4. Последовательность разработки
Системный анализ объекта
Разработка системы переменных
Математическое описание связей между переменными
Предварительное обоснование значений параметров
Упрощение математического описания
Программирование
Отладка модели
Параметрическая идентификация
Опытная эксплуатация
Слайд 10Технология разработки имитационных моделей аграрных систем^p(c) Н.М. Светлов, 2006.
5. Требования к
Соотношения должны быть разрешимы относительно любой переменной, если другие переменные заданы, причём решение должно быть единственным
Соотношения должны иметь простой и понятный экономический смысл
Соотношения не должны быть слишком длинными
Единицы измерения всех слагаемых уравнений, имеющих форму Σi f(xi) = 0, должны быть одинаковыми
Преимущество надо отдавать соотношениям непрерывным и дифференцируемым