- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Целевое программирование. (Лекция 5) презентация
Содержание
- 1. Целевое программирование. (Лекция 5)
- 2. ФОРМУЛИРОВКА ЗАДАЧИ ЦЕЛЕВОГО ПРОГРАММИРОВАНИЯ Файрвилл
- 3. 1. Налоговые поступления должны составить не менее
- 4. Обозначим: через хн, хр и хо ставки
- 5. После упрощения получаем три ограничения: Каждое из
- 6. Сначала каждое неравенство преобразуется в частную задачу,
- 7. Определенные значения отклоняющих переменных s+ и s-
- 8. Поэтому ведется поиск такого компромиссного решения, которое
- 9. Метод весовых коэффициентов Пусть что модель
- 10. Новое рекламное агентство, в составе которого 10
- 11. Реклама на радио и телевидении
- 12. Обозначим через x1, и х2 количество минут
- 13. Менеджеры рекламного агентства считают, что выполнение условия
- 14. Метод приоритетов В методе приоритетов n частных
- 15. В методе приоритетов поочередно решаются задачи с
- 16. Вычислительный алгоритм Этап 0. Определяем частные целевые
- 17. Предположим, что наибольший приоритет имеет частная целевая
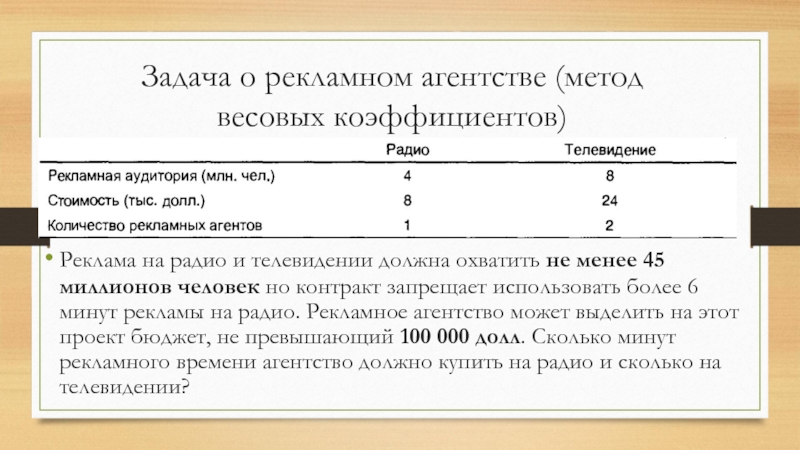
- 18. Задача о рекламном агентстве (метод приоритетов)
- 19. Оптимальное решение этой задачи составляет х1 =
- 20. Цель 1. Максимизировать объем рекламной аудитории (Р1)
- 21. Этап 1.
- 22. Метод идеальной точки решения линейных двухкритериальных задач
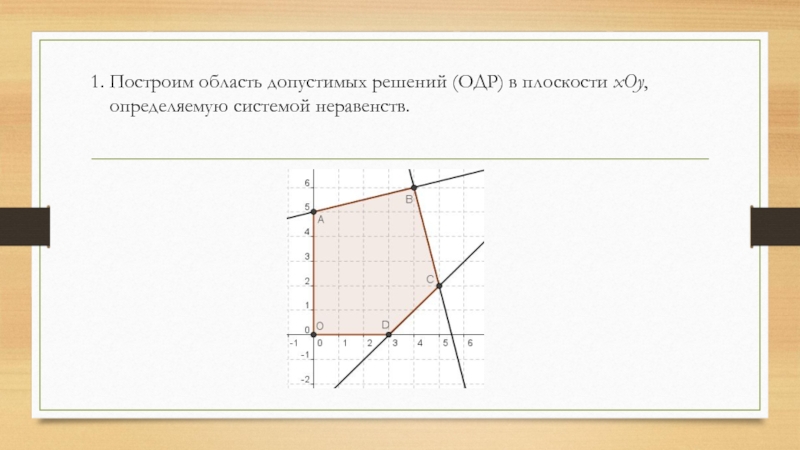
- 23. 1. Построим область допустимых решений (ОДР) в плоскости xOy, определяемую системой неравенств.
- 24. 2. Построим в критериальной плоскости область, соответствующую
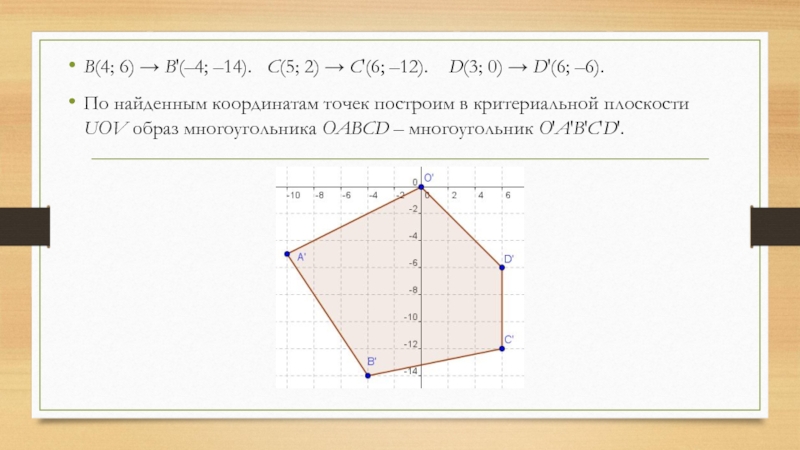
- 25. B(4; 6) → B′(–4; –14). C(5;
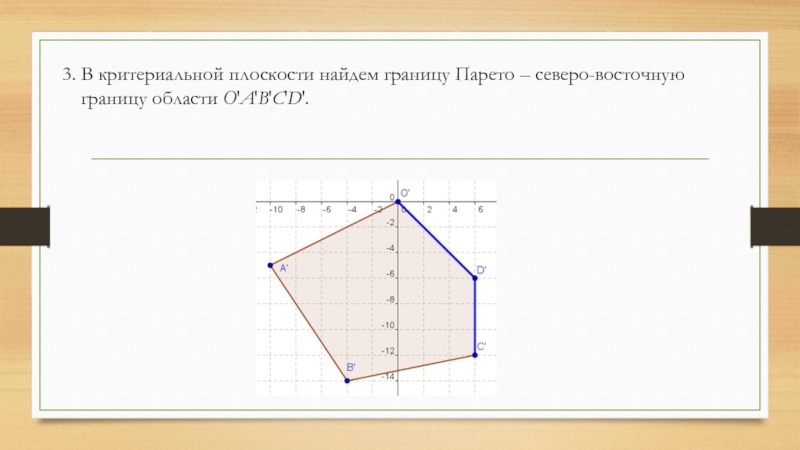
- 26. 3. В критериальной плоскости найдем границу Парето – северо-восточную границу области O′A′B′C′D′.
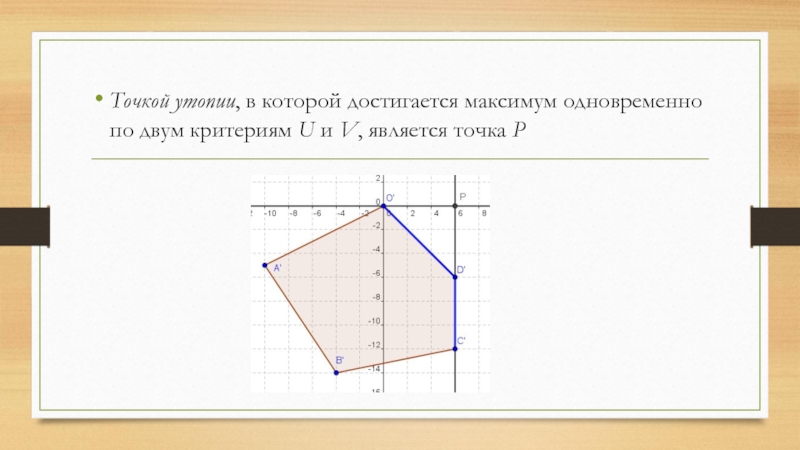
- 27. Точкой утопии, в которой достигается максимум одновременно
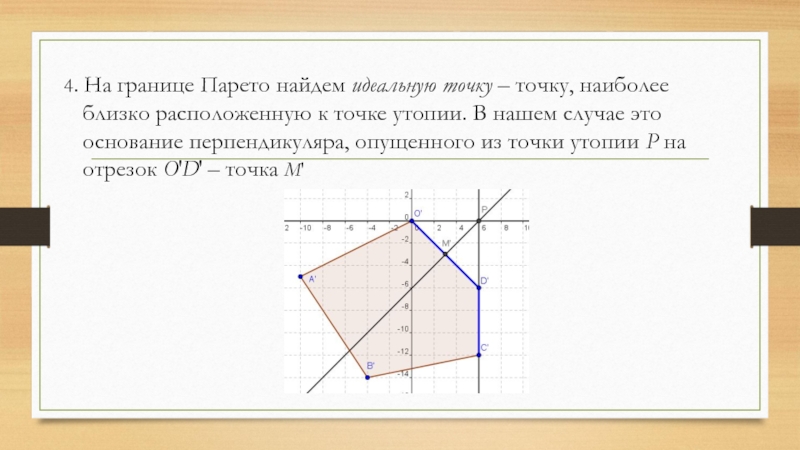
- 28. 4. На границе Парето найдем идеальную точку
- 29. Найдем координаты точки M′. Для этого найдем
- 30. Найдем уравнение перпендикуляра, опущенного из точки утопии
- 31. Т.е.: М′(3; –3), а значит компромиссное решение
Слайд 2ФОРМУЛИРОВКА ЗАДАЧИ ЦЕЛЕВОГО
ПРОГРАММИРОВАНИЯ
Файрвилл — небольшой городок, в котором проживает
Ежегодная база налогообложения недвижимости составляет 550 миллионов дол.
Ежегодная база налогообложения розничных и оптовых продаж составляет 35 и 55 миллионов дол. соответственно.
Ежегодное потребление городом бензина оценивается в 7,5 миллионов галлонов.
Городской совет планирует разработать систему налоговых ставок, основанную на перечисленных базах налогообложения и учитывающую следующие ограничения и требования.
Слайд 31. Налоговые поступления должны составить не менее 16 миллионов долларов от
2. Налог с розничных продаж не может превышать 10% от суммы всех собираемых налогов.
3. Налог с оптовых продаж не может превышать 20% от суммы всех налогов.
4. Налог на бензин не может превышать 2 центов за галлон.
Слайд 4Обозначим: через хн, хр и хо ставки налогов (выраженные десятичными дробями)
Пожелания городского совета можно записать следующим образом
Слайд 5После упрощения получаем три ограничения:
Каждое из этих неравенств представляет одну из
Слайд 6Сначала каждое неравенство преобразуется в частную задачу, в рамках которой можно
Неотрицательные переменные s+ и s- называются отклоняющими
Отклоняющие переменные зависимы по определению, поэтому они обе одновременно не могут быть базисными.
Слайд 7Определенные значения отклоняющих переменных s+ и s- либо соответствуют ограничению, либо
Хорошее компромиссное решение минимизирует число невыполняемых ограничений.
В нашем примере первые три ограничения являются неравенствами типа ">", а четвертое— неравенством типа "<".
Вследствие этого положительные значения отклоняющих переменных s+1 , s+2, s+3, s -4 будут указывать на то, что соответствующие ограничения не выполняются.
Слайд 8Поэтому ведется поиск такого компромиссного решения, которое будет удовлетворять по возможности
Минимизировать G1 = s+1
Минимизировать G2 = s+2
Минимизировать G3 = s+3
Минимизировать G4 = s -4
Слайд 9Метод весовых коэффициентов
Пусть что модель целевого программирования имеет n целей
Минимизировать Gi, i = 1, 2,..., n.
В методе весовых коэффициентов обобщенная целевая функция определяется следующим образом:
Минимизировать z = wlGl + w2G2 + ... + wnGn.
Здесь wi (i = 1, 2, ..., n)— положительные весовые коэффициенты, которые отображают предпочтения, отдаваемые каждой цели.
Например, вариант wi = 1 для всех i говорит о равнозначности всех целей.
Слайд 10Новое рекламное агентство, в составе которого 10 рекламных агентов, получило контракт
Задача о рекламном агентстве (метод весовых коэффициентов)
Слайд 11
Реклама на радио и телевидении должна охватить не менее 45 миллионов
Задача о рекламном агентстве (метод весовых коэффициентов)
Слайд 12Обозначим через x1, и х2 количество минут рекламного времени, закупленного соответственно
Минимизировать Gl = s+1 (для выполнения условия по рекламной аудитории),
минимизировать G2 = s -2 (для выполнения условия по бюджету)
Слайд 13Менеджеры рекламного агентства считают, что выполнение условия по объему рекламной аудитории
Минимизировать z = 2G1 + G2 = 2 s+1 + s -2
Оптимальное решение этой задачи:
z = 10, x1 = 5 минут, x2 = 2,5 минуты, s+1 = 5 миллионов человек.
Остальные переменные равны нулю.
Так как s+1 = 5, значит, объем рекламной аудитории меньше запланированного на 5 миллионов. При этом условие по бюджету выполнено, поскольку s -2 = 0.
Методы целевого программирования позволяют получить только эффективное решение задачи, которое не всегда будет оптимальным. Например, решение х1 = 6 и х2 = 2 дает такой же объем рекламной аудитории, но при меньшей стоимости рекламной кампании (8 х1 + 24 х2 = 96 000 долл.).
Слайд 14Метод приоритетов
В методе приоритетов n частных целевых функций ранжируются в порядке
минимизировать G1 = ρ1 (наивысший приоритет),
…
минимизировать Gn =ρn (наинизший приоритет).
Переменные ρi — это компоненты отклоняющих переменных, т.е. 5/ или s s+i и s-i , которые определяют i-ю целевую функцию.
Слайд 15В методе приоритетов поочередно решаются задачи с одной целевой функцией, начиная
В процессе решения последовательных задач решение задачи с целевой функцией, имеющей более низкий приоритет, не может ухудшить полученные ранее решения задач с целевой функцией, имеющих более высокий приоритет.
Это означает, что если z(Gi) — оптимальное значение целевой функции Gi, то для всех i >=1 оптимизация любой целевой функции Gj (j > i с меньшим приоритетом не может ухудшить значение z(Gi).
Слайд 16Вычислительный алгоритм
Этап 0. Определяем частные целевые функции задачи и ранжируем их
рядке приоритетов: G1 = ρ1 >G2 = ρ2 … > Gn = ρn. Положим i = 1.
Этап i. Решаем i-ю задачу ЛП с целевой функцией Gi. Обозначим через ρ* полученное оптимальное значение отклоняющей переменной ρi.
Если i = n, вычисления заканчиваются, поскольку решена последняя n-я задача. В противном случае вводим в задачу новое ограничение ρi = ρ*, тогда значение ρi не сможет измениться при решении последующих задач.
Полагаем i = i + 1 и повторяем этап i
Слайд 17Предположим, что наибольший приоритет имеет частная целевая функция, соответствующая условию, налагаемому
Этап 0. G1 > G2, где
G1 : минимизировать s+1 (условие по рекламной аудитории),
G2: минимизировать s-2 (условие по бюджету).
Задача о рекламном агентстве (метод приоритетов)
Слайд 18Задача о рекламном агентстве (метод приоритетов)
Этап 1. Решаем первую задачу ЛП:
Минимизировать
при выполнении ограничений:
Слайд 19Оптимальное решение этой задачи составляет х1 = 5 минут, х2 =
Решение показывает, что условие по объему рекламной аудитории не выполняется с дефицитом в 5 млн. чел.
В этой задаче мы имеем ρ1 = s+1 , поэтому в следующей задаче добавим ограничение s+1 = 5 .
Этап 2. Минимизировать G1 = s-2
при выполнении тех же ограничений, что и в предыдущей задаче, плюс дополнительное ограничение s+1 = 5 .
Но в в решении второй задачи нет необходимости, поскольку уже в решении первой имеем s-2 = 0. Следовательно, решение первой задачи автоматически является оптимальным решением второй. Решение s-2 = 0 показывает, что ограничение, касающееся бюджета рекламной компании, выполняется.
Слайд 20Цель 1. Максимизировать объем рекламной аудитории (Р1)
Цель 2. Минимизировать стоимость рекламной
Максимизировать Р1 = 4х1, + 8х2,
минимизировать Р2 = 8x1, + 24х2.
при ограничениях
Задача о рекламном агентстве («истинные целевые функции» и метод приоритетов)
Слайд 21Этап 1.
Оптимальное решение этой задачи: х1 = 0, х2 = 5 и Р1 = 40. Отсюда видно, что объем рекламной аудитории не может превысить 40 миллионов человек.
Этап 2. Минимизировать Р2 = 8x1, + 24х2,
Р2 = 96 000 долл., х1 = 6 минут и х2 = 2 минуты. Получили тот же объем рекламной аудитории (Р1 = 40 млн. чел.), но за меньшую стоимость.
Слайд 22Метод идеальной точки решения линейных двухкритериальных задач оптимизации
U = 2х – 2у → max
V = –2x – y →
4y – x ≤ 20;
4x + y ≤ 22;
х – у ≤ 3;
х ≥ 0; у ≥ 0
Слайд 231. Построим область допустимых решений (ОДР) в плоскости xOy, определяемую системой
Слайд 242. Построим в критериальной плоскости область, соответствующую области допустимых решений OABCD.
В нашем случае: O(0; 0), A(0; 5), B(4; 6), C(5; 2), D(3; 0).
Найдем координаты образов точек O, A, B, C, D в линейном преобразовании, определяемом целевыми функциями:
O(0; 0):
O(0; 0) → O′(0; 0).
A(0; 5):
A(0; 5) → A′(–10; –5).
Слайд 25B(4; 6) → B′(–4; –14). C(5; 2) → C′(6; –12).
По найденным координатам точек построим в критериальной плоскости UOV образ многоугольника OABCD – многоугольник O′A′B′C′D′.
Слайд 263. В критериальной плоскости найдем границу Парето – северо-восточную границу области O′A′B′C′D′.
Слайд 27Точкой утопии, в которой достигается максимум одновременно по двум критериям U
Слайд 284. На границе Парето найдем идеальную точку – точку, наиболее близко
Слайд 29Найдем координаты точки M′. Для этого найдем уравнение прямой O′D′. Воспользуемся
O′(0; 0), D′(6; –6)
Слайд 30Найдем уравнение перпендикуляра, опущенного из точки утопии P на отрезок O′D′.
Координаты точки М′:
,
Слайд 31Т.е.: М′(3; –3), а значит компромиссное решение позволит достигнуть значений целевых
5. Найдем координаты точки в плоскости xOy, которой соответствует точка М′ критериальной плоскости. Для этого решим систему уравнений:
Получили, что компромиссным решением метода идеальной точки является M(1,5; 0), в которой критерии достигают значений U = 3, V = –3.
Эта точка принадлежит отрезку OD
Ответ: M(1,5; 0), U = 3, V = –3.