- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
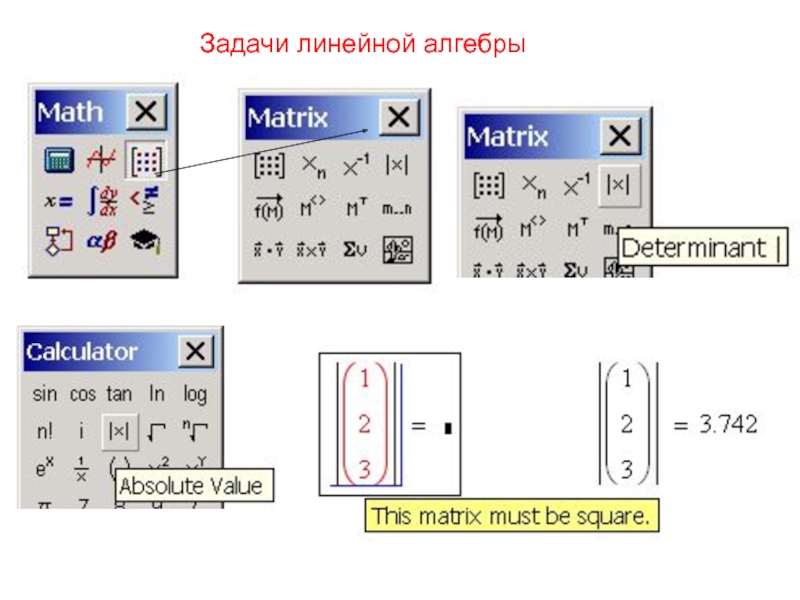
Задачи линейной алгебры. Решение дифференциальных уравнений в MathCAD презентация
Содержание
- 1. Задачи линейной алгебры. Решение дифференциальных уравнений в MathCAD
- 4. Матричные функции Первая группа matrix(m, n,
- 6. Вторая группа last(v) length(v) min(v),
- 7. Третья группа rref(A) rank(A) eigenvals(A) eigenvecs (A) eigenvec(A,e) normi(A) lsolve (A,b)
- 9. Решение систем линейных алгебраических уравнений
- 10. Метод Гаусса
- 11. Метод Крамера Рассмотрим случай, когда определитель матрицы равен нулю. Решение проводится методом Гаусса
- 13. Решение дифференциальных уравнений в MathCAD Решение
- 14. Вектор первых производных Вектор
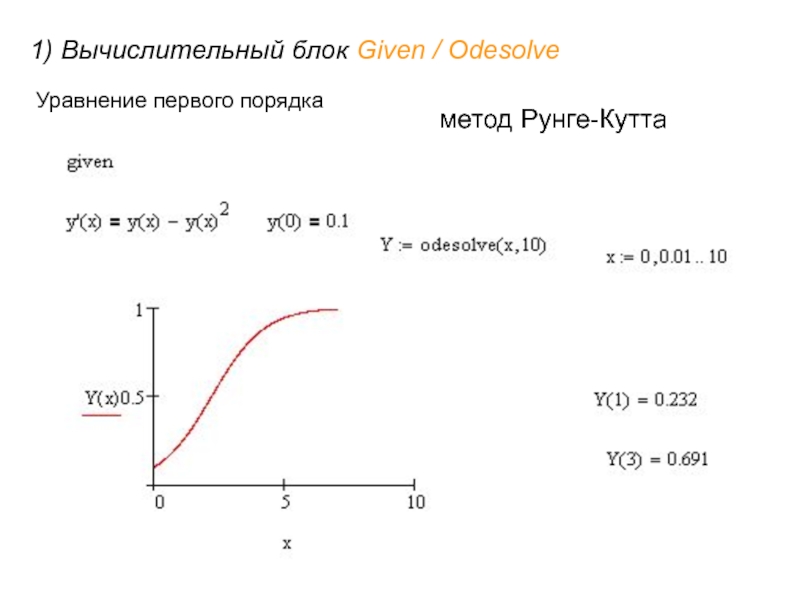
- 15. 1) Вычислительный блок Given / Odesolve Уравнение первого порядка метод Рунге-Кутта
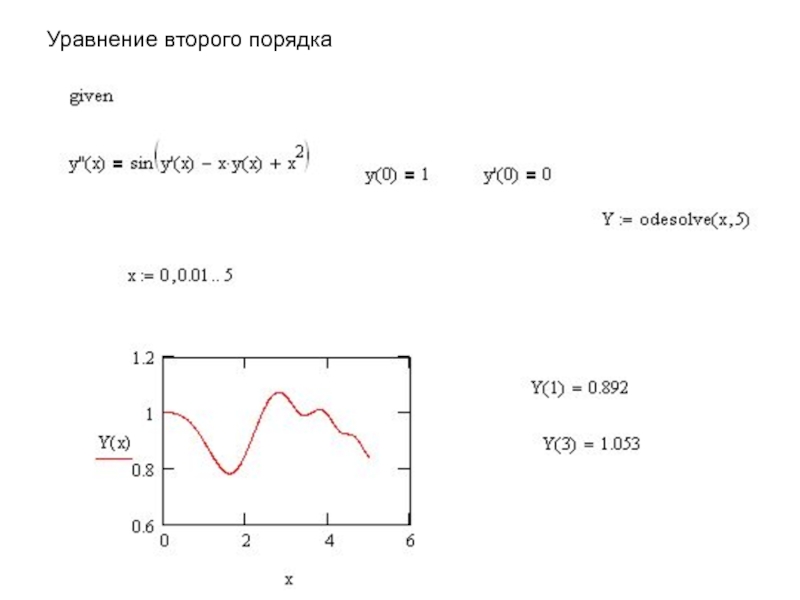
- 16. Уравнение второго порядка
- 17. 2) Альтернативный метод решения ОДУ
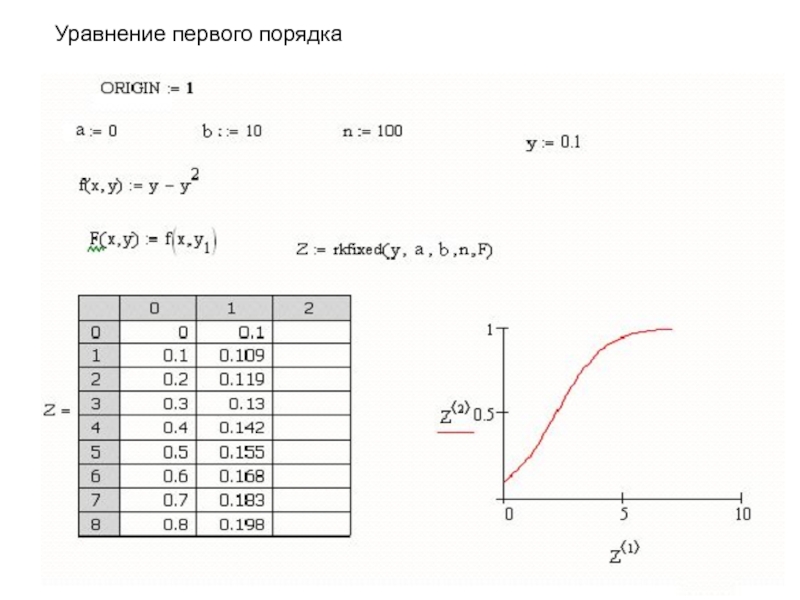
- 18. Уравнение первого порядка
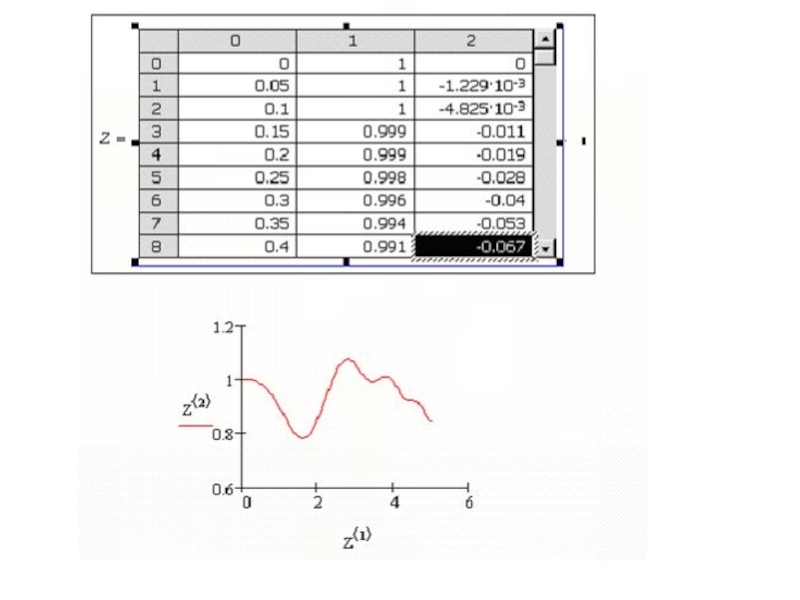
- 19. Уравнение второго порядка
- 21. Решение систем ОДУ 1) Блок Given
Матричные функции Первая группа matrix(m, n, f) diag(v) identity(n) augment(A, B) stack(A, B) submatrix(A, ir, jr, ic, jc)
Слайд 4Матричные функции
Первая группа
matrix(m, n, f)
diag(v)
identity(n)
augment(A, B)
stack(A, B)
submatrix(A, ir, jr, ic,
jc)
Слайд 6Вторая группа
last(v)
length(v)
min(v), max(v)
Re(v)
Im(v)
sort(V)
reverse (sort(v))
csort (A,n)
rsort (A,n)
rows(A)
cols(A)
max(A), min(A)
tr(A)
mean(A)
Слайд 9
Решение систем линейных алгебраических уравнений
Неоднородная система уравнений
Определитель матрицы не
равен нулю, тогда
три способа решения: 1) Метод обратной матрицы
2) Метод Гаусса
3) Метод Крамера
три способа решения: 1) Метод обратной матрицы
2) Метод Гаусса
3) Метод Крамера
Слайд 11Метод Крамера
Рассмотрим случай, когда определитель матрицы равен
нулю. Решение проводится методом
Гаусса
Слайд 13Решение дифференциальных уравнений в MathCAD
Решение Обыкновенных Дифференциальных Уравнений (ОДУ)
ОДУ
первого порядка
F(x,y,y’)=0
F(x,y(x),y’(x))=0
y’=f(x,y)
ОДУ высших порядков
F(x,y,y’,y’’, …,y(n))=0
F(x, y(x), y’(x), y’’(x),…, y(n)(x))=0
Y(n) =f(x, y, y’, …, y(n-1))
Y’ = F(x, Y), Y(x0) = Y0
Слайд 172) Альтернативный метод решения ОДУ
с помощью встроенных функций
:
rkfixed, Rkadapt, или Bulstoer
rkfixed, Rkadapt, или Bulstoer
rkfixed – метод Рунге-Кутта с фиксированным шагом интегрирования.
Rkadapt – метод Рунге-Кутта с переменным шагом интегрирования.
Bulstoer – метод Булирша – Штера
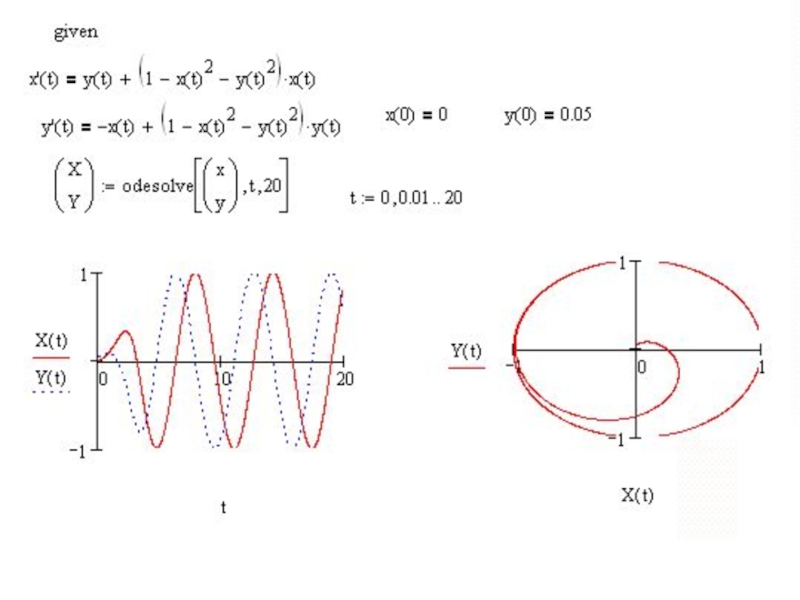
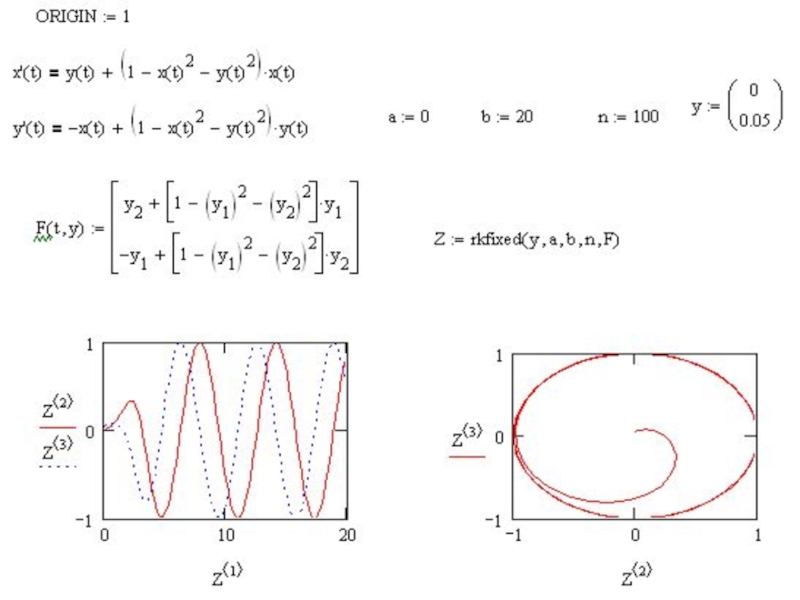
Слайд 21Решение систем ОДУ
1) Блок Given / Odesolve
2) Встроенные функции
rkfixed, Rkadapt и Bulstoer
